2022. 4. 13. 20:00ㆍMajor`/알고리즘
Divide-and-Conquer
1. 일단 자르기 : Divide
2. 자른 subProblem들에 대한 해답은 Recursion으로 : Conquer
3. Recursion으로부터 얻어진 결과들을 종합/정리 : Combine
1) Merge Sort
가장 기본적인 "Divide and Conquer" 기법을 사용하는 정렬 알고리즘이다
static void Merge_Sort(int [] list, int left, int right){
if(left < right){
int mid = (left + right) / 2;
Merge_Sort(list, left, mid);
Merge_Sort(list, mid + 1, right);
Merge(list, left, mid, right);
}
}1. Divide
"mid"를 기준으로 양쪽 sublist들을 MergeSort한다
2. Conquer
1)에서 Divide한 양쪽 sublist들을 Recursion을 보내버리고
→ Recursion에서 각 sublist들은 정렬이 알아서 잘 될 것이다 (Recursion Fairy)
3. Combine
2)에서 "알아서" 정렬된 sublist들을 Merge시킨다
static void Merge(int [] list, int left, int mid, int right){
int [] buffer = new int[list.length]; // [left, right] Sort Buffer
int leftIndex = left;
int rightIndex = mid + 1;
int bufferIndex = left;
while(leftIndex <= mid && rightIndex <= right){
if(list[leftIndex] < list[rightIndex]){
buffer[bufferIndex++] = list[leftIndex++];
}
else{
buffer[bufferIndex++] = list[rightIndex++];
}
}
if(leftIndex > mid){
while(rightIndex <= right){
buffer[bufferIndex++] = list[rightIndex++];
}
}
else{
while(leftIndex <= mid){
buffer[bufferIndex++] = list[leftIndex++];
}
}
for(int i=left; i<=right; i++){
list[i] = buffer[i];
}
}
시간복잡도 분석
일단 Merge를 보면 O(n)으로 간단히 구할 수 있다
그리고 MergeSort를 보면
static void Merge_Sort(int [] list, int left, int right){
if(left < right){
int mid = (left + right) / 2;
Merge_Sort(list, left, mid);
Merge_Sort(list, mid + 1, right);
Merge(list, left, mid, right);
}
}"T(n)을 MergeSort의 수행 시간에 대한 함수"라고 정의한다면

2) Quick Sort
Quick Sort도 Merge Sort와 비슷한 D & C Sort Algorithm인데 약간의 차이는 존재한다
MergeSort
mid를 기준으로 양쪽으로 list를 나눈 뒤, 각 list들을 정렬 한 후 최종적으로 Merge
QuickSort
pivot이라는 값을 기준으로 왼쪽 = pivot보다 작은 값 & 오른쪽 = pivot보다 큰 값으로 일단 정렬
이후 pivot 기준 양쪽을 정렬해준다
static void Quick_Sort(int [] list, int left, int right){
if(left < right){
int pivot = Partition(list, left, right);
Quick_Sort(list, left, pivot - 1);
Quick_Sort(list, pivot + 1, right);
}
}static int Partition(int [] list, int left, int right){
int mid = (left + right) / 2;
int pivot = list[mid];
swap(list, mid, right);
int pivotIndex = left - 1; // pivotIndex : 최종적인 Pivot의 위치
for(int i=left; i<right; i++){
if(list[i] < pivot){
pivotIndex++;
swap(list, i, pivotIndex);
}
}
swap(list, right, pivotIndex + 1);
return pivotIndex + 1;
}Partition의 목적은 앞에서 정의한 "pivot"의 "list에서의 위치"를 return해주는 함수이다

시간복잡도 분석
Partition도 어차피 for문 1번이므로 O(n)이라고 쉽게 구할 수 있다
그리고 QuickSort를 보면
static void Quick_Sort(int [] list, int left, int right){
if(left < right){
int pivot = Partition(list, left, right);
Quick_Sort(list, left, pivot - 1);
Quick_Sort(list, pivot + 1, right);
}
}"T(n)을 QuickSort의 수행 시간에 대한 함수"라고 정의한다면
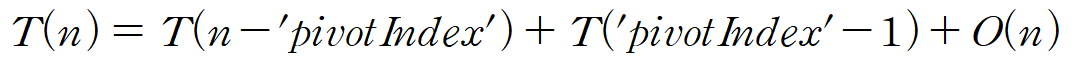
결국 "처음 정의한 pivot의 위치"에 의해서 T(n)은 결정된다
Best Case
당연히 pivot이 중앙에 있을 때가 best이다

Worst Case
Worst는 pivot이 처음 or 마지막에 위치할 경우이다
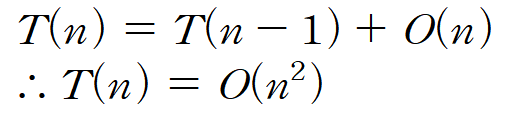
3) Split-Multiplication

초.중.고때 사용하던 일반적인 "곱셈 알고리즘"은 그냥 단순히 각 숫자들 하나하나 곱해주는 거고 이것은 결국 N자리 숫자면 N자리 덧셈을 N번 한다는 의미이다
따라서 이경우 시간복잡도는 O(n2)이다
하지만 이걸 일반화 시켜서 풀어본다면 시간복잡도가 더 좋아지는 경우도 생길 것이다
N자리 정수 간의 곱셈을 가정해보자
예를 들어서 1234 X 5678은 그냥 단순히 하나하나 곱해보면 결과는 나올 것이다
하지만 1234 & 5678을 어떤 정해진 형식에 의해서 수를 변경시켜본다면?
1234는 4자리 정수로써 이를 변경시켜보면 (12 X 100) + 34로 변경이 가능할 것이다
이걸 좀더 일반화 해보자면 다음과 같다

결국 N자리 정수끼리의 곱셈은 다음과 같이 형식화 할 수 있다
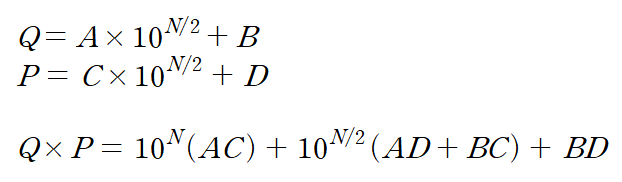
static int Solution(int x, int y, int N){
if(x < 10 && y < 10){
return x*y;
}
int M = (int) (Math.ceil((double)N/2));
/*
N이 홀수일 경우
>> 나눌 때 left가 right보다 길이가 길게 나눠주기
*/
int a = (int) (x / (Math.pow(10, M)));
int b = (int) (x % (Math.pow(10, M)));
int c = (int) (y / Math.pow(10, M));
int d = (int) (y % (Math.pow(10, M)));
int e = Solution(a, c, M);
int f = Solution(a, d, M);
int g = Solution(b, c, M);
int h = Solution(b, d, M);
return (int) (Math.pow(10, 2*M) * e + Math.pow(10, M) * (f + g) + h);
}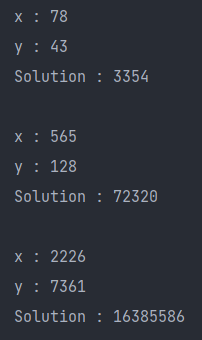
시간복잡도 분석
"T(n)을 Solution의 수행 시간에 대한 함수"라고 정의한다면
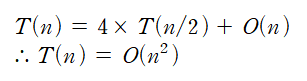
이렇게 나누어도 시간복잡도가 일반적 곱셈과 동일하다
시간복잡도를 더 줄일 방법은 존재하지 않을까?
>> Karatsuba Algorithm
4) Karatsuba Algorithm (Fast Multiplication)

이전의 Split Multiplication은 결국 재귀를 4번 돌림으로써 일반적 곱셈 알고리즘과 동일한 시간복잡도가 나왔다
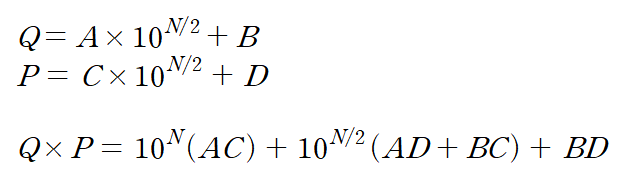
여기서 식을 약간 변형시켜보자면

결국 필요한 곱셈은 ac / bd / (a+b)(c+d) :: 3개로 줄어들었다
static int Karatsuba_Solution(int x, int y, int N){
if(x < 10 && y < 10){
return x*y;
}
int M = (int) (Math.ceil((double)N/2));
/*
N이 홀수일 경우
>> 나눌 때 left가 right보다 길이가 길게 나눠주기
*/
int a = (int) (x / (Math.pow(10, M)));
int b = (int) (x % (Math.pow(10, M)));
int c = (int) (y / Math.pow(10, M));
int d = (int) (y % (Math.pow(10, M)));
/*
(a+b)(c+d) = ac + (ad + bc) + bd
(ad + bc) = (a+b)(c+d) - (ac + bd)
>> ac + {(a+b)(c+d) - (ac + bd)} + bd
*/
int e = Karatsuba_Solution(a, c, M);
int f = Karatsuba_Solution((a+b), (c+d), M);
int g = Karatsuba_Solution(b, d, M);
return (int) (Math.pow(10, 2*M) * e + Math.pow(10, M) * (f - (e+ g)) + g);
}
시간복잡도 분석
"T(n)을 Karatsuba_Solution의 수행 시간에 대한 함수"라고 정의한다면
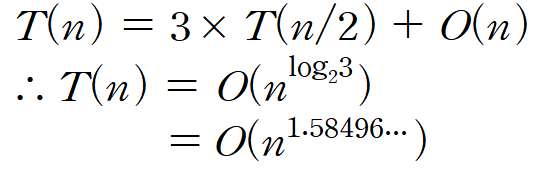
5) Matrix Multiplication




6) Binary Search

Binary Search는 간단하게 "K"라는 정수를 list에서 찾는 알고리즘인데 list에 K가 없으면 return -1을 해주면 된다
다른말로 "이분 탐색"이라고도 한다
왜냐하면 list를 절반으로 나누어서 list[mid]와 K를 비교해서 왼쪽을 탐색할지 오른쪽을 탐색할지 결정하기 때문이다
※ Binary Search는 "반드시 정렬된 배열"에서 수행된다
static int BinarySearch_Solution(int [] list, int left, int right, int target){
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
if(list[mid] < target){
return BinarySearch_Solution(list, mid + 1, right, target);
}
else if(list[mid] > target){
return BinarySearch_Solution(list, left, mid - 1, target);
}
else{
return mid;
}
}

시간복잡도 분석
"T(n)을 BinarySearch_Solution의 수행 시간에 대한 함수"라고 정의한다면
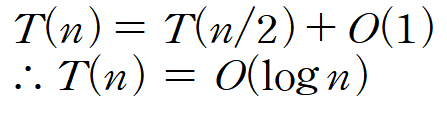
7) Selection : Quick_Select

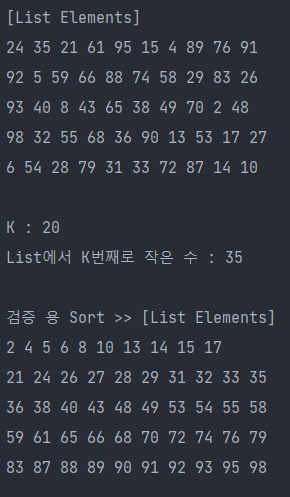
Selection문제란 list에서 "K번째로 작은 수"를 찾는 탐색 알고리즘이다
QuickSort와 비슷한 메커니즘으로 동작한다 :: Partition
static int QuickSelect(int [] list, int left, int right, int K){
if(left > right){
return -1;
}
int pivotIndex = Partition(list, left, right); // O(n)
if(pivotIndex < K){
return QuickSelect(list, pivotIndex + 1, right, K);
}
else if(pivotIndex > K){
return QuickSelect(list, left, pivotIndex - 1, K);
}
else{
return list[pivotIndex];
}
}임의로 정한 pivot의 위치를 Partition으로 return받는다
만약 pivotIndex가 K보다 작다?? 이 의미는 K번째로 작은 수가 pivotIndex의 오른쪽에 존재한다는 의미이다
static int Partition(int [] list, int left, int right){
int mid = (left + right) / 2;
int pivot = list[mid];
swap(list, mid, right);
int pivotIndex = left - 1;
for(int i=left; i<right; i++){
if(list[i] < pivot){
pivotIndex++;
swap(list, pivotIndex, i);
}
}
swap(list, pivotIndex + 1, right);
return pivotIndex + 1;
}
시간복잡도 분석
"T(n)을 QuickSelect의 수행 시간에 대한 함수"라고 정의한다면

이것또한 "pivot의 위치"에 따라 T(n)이 결정된다
Best Case
당연히 pivot이 중앙에 있는 경우이다
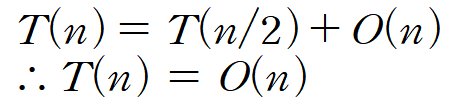
Worst Case
pivot이 양 끝에 위치할 경우이다
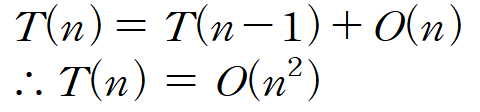
8) Selection : MOM_Select

앞에서 Quick_Select를 할 때 "pivot 고르기"를 먼저 하였다
그리고 pivot의 위치에 의해서 시간복잡도가 결정되는 것을 확인할 수 있었다
>> Good Pivot이란??
"대략 list의 중간 쯤에 위치한 원소"
예를 들어서 말하자면 위에 T(n) 점화식에서 T(n/r)의 꼴로 나타난다면 좋은 pivot이라고 할 수 있다
이 의미는 결국 0 < a < 1에 대해서 pivotIndex = an인 pivot을 고른다는 의미와 동일하다

Median-Of-Medians
1. list의 원소 n개를 5개씩 묶어서 n/5개의 block으로 나누기
2. 각 block의 median을 구한다
3. 전체적인 block의 median들 중에서 median을 최종적으로 구한다 (Median-Of-Medians)
4. 최종적 median을 pivot으로 사용한다

이렇게 [n/5]개의 block과 가운데에 MOM이 있다고 하자
그러면 MOM보다 작은 element의 개수는 몇개일까?


MOM은 결국 원래 문제인 A[1,2,..n]에서 K번째 수 찾기를 Reduction한 "M[1,2,...m]에서 m/2번째 수 찾기"이다
따라서 m은 n/5이므로 MOM은 대략 "n/10"위치에 있다고 생각할 수 있다
>> 이를 통해서 동일 line에서 MOM은 대략 [n/10]개의 element보다는 크다고 판단할 수 있다

결국 전체적으로 MOM보다 작은 element는 [3n/10]개 존재한다고 할 수 있다
그러면 MOM보다 큰 element는? 대략 [7n/10]개 존재한다고 할 수 있다

>> 아까 가정한대로 "pivotIndex = an"꼴이므로 MOM은 Good Pivot이라고 할 수 있다

시간복잡도 분석
static int MOMSelection_(int [] list, int left, int right, int K){
if((right - left) <= 25){
Arrays.sort(list);
return list[K-1];
/*
배열의 원소가 25개 이하면 그냥 정렬 하고 return해주는게 더 빠르다
*/
}
int divideCount = (int)Math.ceil((double)(list.length)/5); // list를 5개씩 나눌 때 총 나눠진 list 개수
int [] buffer = new int[divideCount]; // 각 sublist중 중앙값 저장할 buffer
for(int i=0; i<buffer.length; i++){
buffer[i] = MedianOfFive(list, 5*i, 5*i + 4);
}
int MOM = MOMSelection_(buffer, 0, buffer.length - 1, (buffer.length) / 2);
int pivotIndex = Partition(list, left, right, MOM);
if(pivotIndex < K){
return MOMSelection_(list, pivotIndex + 1, right, K);
}
else if(pivotIndex > K){
return MOMSelection_(list, left, pivotIndex - 1, K);
}
else{
return list[pivotIndex];
}
}
static int MedianOfFive(int [] list, int left, int right){
Arrays.sort(list);
return list[(right + left)/2];
}
static int Partition(int [] list, int left, int right, int pivot){
int currentIndex = left;
for(int i=left; i<=right; i++){
if(list[i] == pivot){
currentIndex = i;
}
}
swap(list, currentIndex, right);
int pivotIndex = left - 1;
for(int i=left; i<right; i++){
if(list[i] < pivot){
pivotIndex++;
swap(list, pivotIndex, i);
}
}
swap(list, pivotIndex + 1, right);
return pivotIndex + 1;
}Recursion은 총 2번 수행한다
→ int MOM
→ return MOMS~~
"T(n)을 MOMSelection_의 수행 시간에 대한 함수"라고 정의한다면
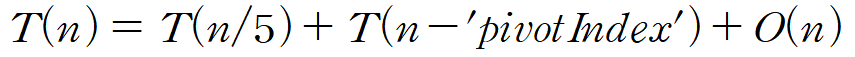

Best Case



Worst Case