[Algorithm Week_4] Recursion Tree 예제
2022. 3. 25. 16:59ㆍMajor`/알고리즘
1) Max
max(A[0, 1, 2, ....., n-1])
// "Base Case"
if n = 1 return A[0]
// 1. Divide
mid <- n/2
// 2. Delegate (Conquer)
m1 <- max2(A[0, 1, 2, ...., mid])
m2 <- max2(A[mid + 1, mid + 2, ..... n-1])
// 3. Combine (Merge)
if m1 > m2
return m1
else
return m2T(n) = 2 X T(n/2) + O(1)
>> T(n) = 2 X T(n/2) + c
▶ Recursion Tree

결국 "value of node"는 해당 node에서 재귀호출을 제외한 비재귀호출의 연산 수행 횟수이고, C번 호출하기 때문에 모든 노드의 value는 C가 된다
이러면 결국 max알고리즘의 수행 시간은 모든 노드의 value의 합으로 볼수있다
leaf노드를 보게되면 n/2k로 나와있고 이 값은 leaf노드이므로 1이 되어야 한다

리프노드의 개수는 2k이고, 리프노드의 개수는 leaf 노드의 비용이라고 판단할 수 있다

>> 따라서 max-알고리즘의 시간복잡도는 O(n)이라고 할 수 있다
▶ Master Theorem
T(n) = 2 X T(n/2) + O(1)
→ r = 2
→ c = 2
→ logcr = 1
이제 f(n)과 nlogcr의 증가속도를 비교해주면 된다

>> 따라서 시간복잡도는 O(n)이라고 할 수 있다
2) Merge Sort
// MergeSort - Pseudo Code
MergeSort(A[1, 2, ..., n]):
if n > 1
// 1. Divide
m <- [n/2]
// 2. Delegate (Conquer)
MergeSort(A[1, 2, ..., m])
MergeSort(A[m+1, m+2, ..., n])
// 3. Combine (Merge)
Merge(A[1, 2, ..., n], m])
// Merge - Pseudo Code
Merge(A[1, 2, 3, ..., n], m):
i <- 1; j <- m + 1
for k <- 1 to n
if j > n
B[k] <- A[i]; i <- i + 1
else if i > m
B[k] <- A[j]; j <- j + 1
else if A[i] < A[j]
B[k] <- A[i]; i <- i + 1
else
B[j] <- A[j]; j <- j + 1
for k <- 1 to n
A[k] <- B[k]T(n) = 2 X T(n/2) + O(n)
>> T(n) = 2 X T(n/2) + cn
▶ Recursion Tree

보게되면 모든 level에서의 cost가 n이다
따라서 mergesort의 수행시간은 n * (트리의 높이)라고 볼 수 있다
>> MergeSort - Time Complexity = O(n log n)
▶ Master Theorem
T(n) = 2 X T(n/2) + O(n)
→ r = 2
→ c = 2
→ logcr = 1
이제 f(n)과 nlogcr의 증가속도를 비교해주면 된다

>> 둘의 증가속도가 비슷하기 때문에 시간복잡도는 O(f(n) X log n) = O(n log n)이라고 볼 수 있다
3) T(n) = 3 X T(n/2) + 4n
▶ Recursion Tree
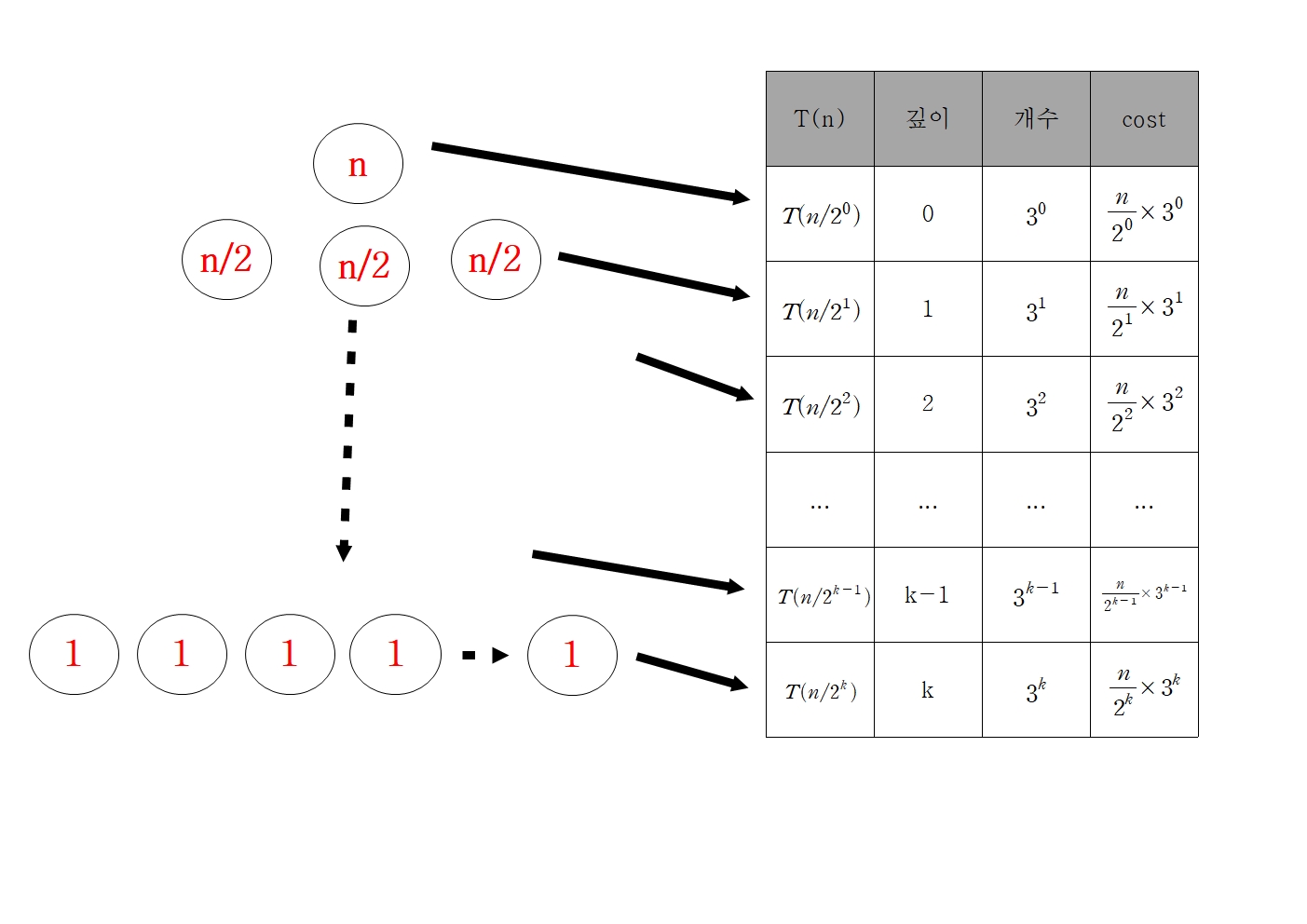
모든 cost를 더해주면 된다

▶ Master Theorem
T(n) = 3 X T(n/2) + 4n
→ r = 3
→ c = 2
→ logcr = log23
이제 f(n)과 nlogcr의 증가속도를 비교해주면 된다

>> 따라서 시간복잡도는 O(nlog23)이라고 할 수 있다
4) T(n) = 4 X T(n/4) + 8
▶ Recursion Tree

모든 cost를 더해주면 된다
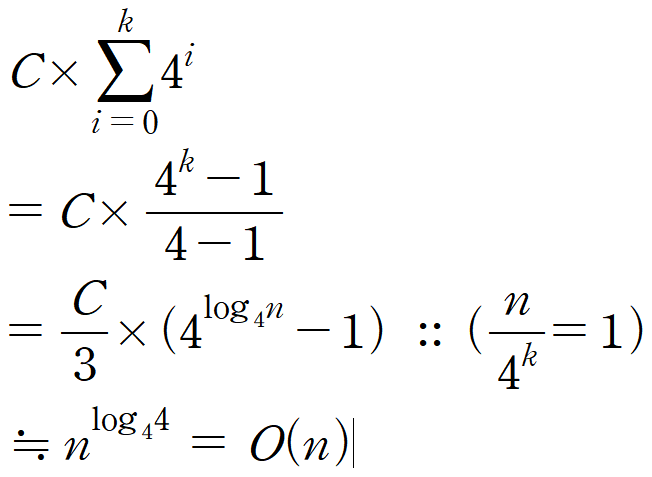
▶ Master Theorem
T(n) = 4 X T(n/4) + 8
→ r = 4
→ c = 4
→ logcr = 1
이제 f(n)과 nlogcr의 증가속도를 비교해주면 된다

>> 따라서 시간복잡도는 O(n)이라고 할 수 있다
5) T(n) = T(n/2) + O(1)
▶ Recursion Tree

각 level별로 1개씩 있으므로 결국 수행 시간은 트리의 높이에 비례한다
>> O(log n)
▶ Master Theorem
T(n) = T(n/2) + O(1)
→ r = 1
→ c = 2
→ logcr = 0
이제 f(n)과 nlogcr의 증가속도를 비교해주면 된다

>> 둘의 증가속도가 비슷하기 때문에 시간복잡도는 O(f(n) X log n) = O(log n)이라고 볼 수 있다
6) T(n) = 2 X T(n/2) + O(n2)
▶ Recursion Tree

모든 cost를 더해주면 된다

▶ Master Theorem
T(n) = 2 X T(n/2) + O(n2)
→ r = 2
→ c = 2
→ logcr = 1
이제 f(n)과 nlogcr의 증가속도를 비교해주면 된다

>> 따라서 시간복잡도는 O(n2)이라고 할 수 있다
7) T(n) = 9 X T(n/2) + O(n3)
▶ Recursion Tree

모든 cost를 더해주면 된다

▶ Master Theorem
T(n) = 9 X T(n/2) + O(n3)
→ r = 9
→ c = 2
→ logcr = log29
이제 f(n)과 nlogcr의 증가속도를 비교해주면 된다

