[Algorithm Week_9&10] DP : Dynamic Programming

[Algorithm Week_3] Recursion

[Algorithm Week_4] Divide & Conquer 개요 - Recursion Tree

[Algorithm Week_6] Backtracking

 

이전에 Recursion을 통해서 문제를 해결해가는 방식을 알아보았고 Recursion을 더 효율적으로 사용하는 Divide & Conquer도 알아봤다

 

하지만 Recursion이 항상 best technique은 아니다

 

왜냐하면 Recursion은 결국 메모리 소모가 많아지고 수많은 Recursive Call 중에는 굉장히 많이 반복되거나 쓸데없는 Call이 존재할 수 있기 때문이다

 

가장 대표적인 Recursion Solution중 하나인 "Fibonacci"에 대해서 알아보면

static int Fibonacci(int n){
    if (n <= 1){
        return n;
    }
    return Fibonacci(n-1) + Fibonacci(n-2);
}

이에 대한 점화식을 표현하면 → "Fibonacci함수에 대한 수행시간 함수를 T(n)이라고 하면"

 

그리고 실제 피보나치 수열에 대한 점화식을 작성해보면

이에 따라서 T(n)과 Fn의 관계를 파악해보면

이러한 결과가 도출이 된다

 

시간복잡도만 봐도 Recursion을 통한 Fibonacci는 굉장히 오랜 시간이 걸리는 것을 파악할 수 있다

더불어서 Recursion_Fibonacci에 대한 Recursion Tree를 그려보면

 

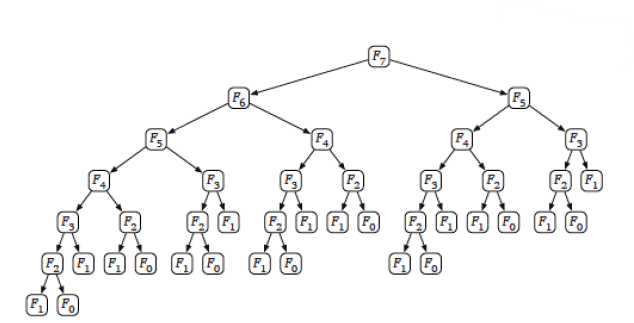
여기서 파악해야할점은 다음과 같다

F5 호출 횟수 : 2회
F3 호출 횟수 : 5회
F2 호출 횟수 : 8회
...
...

 

어차피 계산할 때 우리의 생각으로는 1번만 사용이 되는 값들의 Recursion Call이 굉장히 많고 그에 따라서 메모리 낭비가 굉장히 심해질 것이다

 

여기서 DP를 활용해서 "값들을 저장하고 필요할 때 다시 꺼내자"라는 개념을 가져올 필요가 있다

 

Memoization

Memoization이란 "값의 저장"개념이다

위와 같은 불필요한 Recursive Call을 없애고, 저장되어있는 값을 그냥 사용하기 위한 개념이다

물론 저장된 값이 없다면 그 값을 구해야 하지만, 저장된 값이 있다면 굳이 다시 구할 필요는 없다

당연히 Memoization은 "값을 저장할 Data Structure"가 반드시 필요하다

 

위의 Fibonacci를 Memoization을 활용하면 다음과 같이 변경할 수 있다

 

'''Global Variable'''
static Integer [] buffer = new Integer[n];
buffer[0] = 0;
buffer[1] = 1;

'''Method'''
static int MemoFibonacci(int n){
    if (n <= 1){
        return buffer[n];
    }

    else {
        if (buffer[n] == null) {
            // 저장된 값이 없다면 값 구하기
            return buffer[n] = MemoFibonacci(n - 1) + MemoFibonacci(n - 2);
        } else {
            return buffer[n];
        }
    }
}

Recursion Tree에서 볼 수 있듯이 위에서 Recursion을 활용한 방식은 값을 구하는데 중복이 굉장히 많았는데 Memoization을 활용하니까 불필요한 계산이 없어졌고 그냥 값을 가져다 쓰는 것을 볼 수 있다

 

Memoization_Recursion은 "Top-Down"방식으로 활용되고, Memoization_Iteration은 "Bottom-Up"방식으로 활용된다

static Integer [] buffer = new Integer[100];

static int IterFibonacci(int n){
    buffer[0] = 0;
    buffer[1] = 1;

    for(int i=2; i<=n; i++){
        buffer[i] = buffer[i-1] + buffer[i-2];
    }

    return buffer[n];
}

 

Fibonacci를 Memoization_Iteration방식으로 해결하면 시간복잡도가 O(n)까지 줄어드는것을 확인할 수 있다

---

DP : Dynamic Programming

결국 DP는 중간의 subproblem에 대한 solution을 "저장"한다. 당연히 solution을 "저장"하기 위한 "Data Structure"이 필요하다

보통 Data Structure은 (Array or Table)을 주로 사용한다

 

그리고 DP에서 가장 중요한것은 "올바른 점화식"을 찾는 것이다

올바른 점화식만 찾으면 점화식에 따라서 Table을 채워나가면 된다. 하지만 "점화식을 찾는 과정"이 가장 어려운 단계이다

 

 

DP 과정

1. Formulate the problem "Recursively"

결국 우리가 반드시 알아야하는 것은 "문제를 해결하는 Recursive Algorithm or 점화식"을 찾아내야 한다

 

▶ 1-(a) Specification

우리가 풀고자하는 문제를 "Recursively"하게 묘사해야 한다

이 단계에서는 "문제를 푸는 구체적인 방법"말고 "추상적인 방식"을 묘사하는 것이다

>> "Fn은 n번째 피보나치 수"

 

▶ 1-(b) Solution

1-(a)에서 "추상적인 문제"를 묘사했다면 여기서 "해당 문제에 대한 Algorithm | 점화식"을 설계해야 한다

 

DP에서 점화식없이 문제를 해결할 수가 없다

 

2. Build Solutions to your recurrence from the bottom up

정의한 Problem에 대한 "Base Case"부터 차례대로 table에 쌓아가야 한다

 

▶ 2-(a) Identity the subproblems

1단계로부터 파악한 Problem ~ SubProblem에서 "SubProblem들이 구체적으로 어떤 것이 있는지" 파악을 하는 단계이다

>> Fn을 구하려면 (F0, F1, .... Fn-1)이 필요하고 결국 (0 ~ n) : n+1개가 필요하구나

 

▶ 2-(b) Choose a memoization data structure

이제 Memoization에서 값들을 저장할 "Data Structure"을 정해야 한다

일반적으로 Array를 사용한다

 

▶ 2-(c) Identity Dependencies

그리고 각 SubProblem들은 반드시 그들간의 "의존 관계"가 존재한다

여기서는 각 SubProblem들간의 "의존 관계"가 무엇인지 파악해야 한다

>> "n을 구하려면 n-1 & n-2가 필요하겠구나"

 

▶ 2-(d) Find a good evaluation order

Memoization은 "값을 구해서 저장하고 필요할 때 꺼내서 사용"하는 방식이다

여기서 당연히 값을 구해야 하는데 "값을 구하는 순서"도 굉장히 중요하다

순서는 "각 SubProblem들간의 의존 관계"에 따라서 좋은 순서를 정해주어야 한다

>> "n을 구하려면 n-1 & n-2가 필요하니까 0에서 n까지 Bottom-Up 방식으로 값을 구해야겠다"

 

▶ 2-(e) Analyze space and running time

설계한 구조의 시간 & 공간 복잡도를 분석해야 한다

이것은 1단계에서 보통 파악할 수 있다

 

▶ 2-(f) Write down the algorithm

설계한 방식대로 이제 알고리즘을 작성하면 된다

---

1. LIS

LIS는 "Longest Increasing Subsequence"이고, 주어진 Sequence로부터 "가장 긴 증가하는 부분수열"을 찾는 문제이다

 

31415926535897932384626

이러한 Sequence에서 일단 "3141592653"에서 "1456"이라는 SubSequence까지 도달했다고 하자

 

그러면 우리가 이제 고려해야할점은 남은 "5897932384626"에서 1456에 연결되는 IS를 찾는 것이 문제이다

 

여기서 가장 먼저 보이는 것이 첫번째 숫자인 "5"를 1456에 포함할지 말지이다

이것은 당연히 6보다 작으니까 버리면 된다

 

그러면 다음 숫자이니 "8"을 1456에 포함할지 말지이다

이경우는 2가지 경우의 수가 존재하는데 "8"을 포함하고 계속 찾을지 or "8"을 버리고 다음 부분에서 찾을지이다

(1) Recursion

list[0] = Integer.MIN_VALUE; // Sentinel

static int Solution(int [] list, int i, int j){
    if(j == list.length){
        return 0;
    }

    if(list[i] >= list[j]){
        return Solution(list, i, j+1);
    }
    else{
        int with = Solution(list, j, j+1) + 1;
        int wout = Solution(list, i, j+1);

        return Math.max(with, wout);
    }
}

 

(2) DP

최종적으로 우리가 구하는것은 Solution(0, 1)이다

static int Solution(int [] list, int [][] Memoization, int x, int y){
    for(int i=0; i<list.length; i++){
        Memoization[i][list.length] = 0;
    }

    for(int j=list.length-1; j>=1; j--){
        for(int i=0; i<j; i++){
            int with = Memoization[j][j+1] + 1;
            int wout = Memoization[i][j+1];

            if(list[i] >= list[j]){
                Memoization[i][j] = wout;
            }
            else{
                Memoization[i][j] = Math.max(with, wout);
            }
        }
    }

    return Memoization[x][y];
}

---

2. SubSetSum

SubSetSum은 주어진 TargetNumber "T"를 집합에 존재하는 원소들로 만족시킬 수 있느냐에 대한 문제이다

(1) Recursion

static boolean Solution(int [] list, int index, int T){
    if(T == 0){
        return true;
    }
    else if(index == 0){
        return false;
    }
    else{
        if(list[index] > T){
            return Solution(list, index - 1, T);
        }
        else{
            boolean with = Solution(list, index - 1, T - list[index]);
            boolean wout = Solution(list, index - 1, T);
            return with | wout;
        }
    }
}

 

(2) DP

최종적으로 우리가 구하는것은 Solution(0, T)이다

static boolean Solution(boolean [][] M, int [] list, int index, int T){
    // Base Case
    for(int i=0; i<=T; i++){
        M[list.length][i] = false;
    }

    // Base Case
    for(int i=0; i<list.length; i++){
        for(int j=0; j<=T; j++){
            if(list[i] == j){
                M[i][j] = true;
            }
        }
    }

    for(int i=list.length-1; i>=0; i--){
        /*
        Solution(i, T)를 구하려면 Solution(i+1, T) & Solution(i+1, T-list[i])가 필요
        >> i는 하향탐색 / T는 맘대로
         */
        M[i][0] = true; // 공집합은 항상 만족

        for(int j=1; j<list[i]; j++){
            /*
            T가 list[i]보다 작은 경우는 어차피 list[i]로 만들지 못하기 때문에 다음 영역 탐색
             */
            M[i][j] = M[i+1][j];
        }
        for(int j=list[i]; j<=T; j++){
            M[i][j] = M[i+1][j] | M[i+1][j-list[i]];
        }

    }

    return M[0][T];
}

---

3. LCS

LCS란 "Longest Common Subsequence"로써 Sequence가 2개가 주어지고, 2개의 Sequence의 공통 부분 중 가장 긴 공통 부분을 찾는 문제이다

 

input으로는 2개의 String이 주어지고, output으로는 2개의 string간의 LCS가 도출된다

여기서 문제를 풀기위해서 2개의 String을 각각 배열로 생각하자

 

2개의 배열
- A[1...m]
- B[1...n]

두 배열 A, B는 서로 길이가 동일할 수도 있고 다를 수도 있다

 

여기서 Solution(i, j)라는 함수를 정의하고 이 함수의 의미는 다음과 같다

A[1...i] & B[1...j] 간에 존재하는 LCS의 길이

Base Case는 당연히 {i = 0 or j = 0}이다

 

다른 일반적인 구조는 총 2가지의 경우의수가 존재할 것이다

 

1. A[i] = B[j]

만약 2개가 동일하다면

- 일단 A[i], B[j] 매칭시켜놓고 나머지 부분에서 LCS 찾기

- A[i]에 대한 B[j]의 매칭을 거절하고 B의 나머지 부분에서 A[i]에 매칭될 부분 찾기

• A[1...i] & B[1...j-1]

- B[j]에 대한 A[i]의 매칭을 거절하고 A의 나머지 부분에서 B[j]에 매칭될 부분 찾기

• A[1...i-1] & B[1...j]

 

2. A[i] != B[j]

- A[i]는 여전히 고려하고 B의 나머지 부분에서 A[i]에 매칭될 부분 찾기

• A[1...i] & B[1...j-1]

- B[j]는 여전히 고려하고 A의 나머지 부분에서 B[j]에 매칭될 부분 찾기

• A[1...i-1] & B[1...j]

 

(1) Recursion

static int Solution(char [] a, char [] b, int x, int y){
    if(x == 0 || y == 0){
        return 0;
    }

    if(a[x-1] == b[y-1]){
        int both = Solution(a, b, x-1, y-1) + 1;
        int take_a = Solution(a, b, x-1, y);
        int take_b = Solution(a, b, x, y-1);

        return Math.max(both, Math.max(take_a, take_b));
    }
    else{
        int take_a = Solution(a, b, x-1, y);
        int take_b = Solution(a, b, x, y-1);

        return Math.max(take_a, take_b);
    }
}

 

(2) DP

최종적으로 우리가 구하는 것은 Solution(m, n)이다

• m : A의 길이
• n : B의 길이

static int Solution(int [][] M, char [] a, char [] b, int x, int y){
    // Base Case
    for(int i=0; i<=x; i++){
        M[i][0] = 0;
    }

    for(int i=0; i<=y; i++){
        M[0][i] = 0;
    }

    for(int i=1; i<=x; i++){
        for(int j=1; j<=y; j++){
            if(a[i-1] == b[j-1]){
                int both = M[i-1][j-1] + 1;
                int take_a = M[i][j-1];
                int take_b = M[i-1][j];

                M[i][j] = Math.max(both, Math.max(take_a, take_b));
            }
            else{
                int take_a = M[i][j-1];
                int take_b = M[i-1][j];

                M[i][j] = Math.max(take_a, take_b);
            }
        }
    }

    return M[x][y];
}

---

4. Edit Distance

Edit Distance란 "String A에서 B로 변환하기 위한 최소 편집연산 횟수"를 의미한다

 

편집연산은 다음 3가지가 존재한다

• Insertion
• Deletion
• Substitution

 

Edit Distance의 대표적인 예는 구글 검색이라고 볼 수 있다.

이렇게 구글에서는 edit distance를 이용해서 내가 입력한 문자열이 잘못되었을 경우 가장 근접한 문자열을 제시해준다

 

여기서 Solution(i, j)라는 함수를 정의하고 이 함수의 의미는 다음과 같다

A[1...i] & B[1...j] 간의 Edit Distance

Base Case는 당연히 {m = 0 or n = 0}이다

• i=0 : B를 A에 복사 >> Solution(i, j) = j
• j=0 : A를 B에 복사 >> Solution(i, j) = i

 

다른 일반적인 구조는 총 2가지의 경우의수가 존재할 것이다

 

1. A[i] = B[j]

두 문자가 동일하다는 의미는 굳이 편집 연산을 할 필요가 없다는 의미이다

 

따라서 둘다 이전 영역에 대한 탐색을 진행해주면 된다

• A[1...i-1] & B[1...j-1]

 

2. A[i] != B[j]

만약 두 문자가 다를 경우 고려할 수 있는 편집 연산은 총 3가지이다

 

두 문자열을 배열로 생각 & 위의 문자열 기준

(1) Insertion

위의 문자열이 비어있을 경우 

 

(2) Deletion

아래 문자열이 비어있을 경우

 

(3) Substitution

둘다 비어있지 않을 경우

 

(1) Recursion

static int Solution(char [] a, char [] b, int x, int y){
    if(x == 0){
        return y;
    }

    if(y == 0){
        return x;
    }

    if(a[x-1] == b[y-1]){
        return Solution(a, b, x-1, y-1);
    }
    else{
        int insertion = Solution(a, b, x, y-1);
        int deletion = Solution(a, b, x-1, y);
        int substitution = Solution(a, b, x-1, y-1);

        return Math.min(insertion, Math.min(deletion, substitution)) + 1;
    }
}

 

(2) DP

최종적으로 우리가 구하는 것은 Solution(m, n)이다

• m : A의 길이
• n : B의 길이

static int Solution(int [][] M, char [] a, char [] b, int x, int y){
    for(int i=0; i<=x; i++){
        M[i][0] = i;
    }

    for(int i=0; i<=y; i++){
        M[0][i] = i;
    }

    for(int i=1; i<=x; i++){
        for(int j=1; j<=y; j++){
            if(a[i-1] == b[j-1]){
                M[i][j] = M[i-1][j-1];
            }
            else{
                int insertion = M[i][j-1] + 1;
                int deletion = M[i-1][j] + 1;
                int substitution = M[i-1][j-1] + 1;

                M[i][j] = Math.min(insertion, Math.min(deletion, substitution));
            }
        }
    }

    return M[x][y];
}