[컴퓨터구조론] 2장 연습문제

[컴퓨터구조론] 2장 연습문제

2022. 1. 29. 18:20ㆍSolution`/컴퓨터구조론

[2.1]

클록 주기가 2ns인 CPU가 'ADD addr' 명령어를 인출하고 실행하는 데 걸리는 시간은 모두 몇 ns인가?

"ADD addr"
## 인출 사이클 ##
t(0) : PC -> MAR
t(1) : M[MAR] -> MBR / PC + 1 -> PC
t(2) : MBR -> IF

## 실행 사이클 ##
t(0) : IR(addr) -> MAR
t(1) : M[MAR] -> MBR
t(2) : AC + MBR -> AC

-> 총 6개의 CPU 클록 주기만큼의 시간 = 6 X 2ns = 12ns

[2.2]

인터럽트 서비스 루틴을 수행하는 도중에 더 높은 우선순위를 가진 인터럽트 요구가 들어오더라도 그 루틴의 수행이 중단되지 않도록 하는 방법을 설명하라

ISR을 실행할 때, "인터럽트 불가능" 명령어를 실행하고, ISR이 종료될 때, "인터럽트 가능" 명령어를 실행한다

[2.3]

인터럽트 사이클은 반드시 실행 사이클이 종료된 다음에 수행되어야 하는 이유는 무엇인가? 만약 인출된 명령어를 위한 실행 사이클이 수행되는 도중에 들어오는 인터럽트 요구에 대하여 CPU가 즉시 응답을 한다면, 어떤 문제가 발생하게 되는가?

[현재 실행중인 명령어 : C1 / 현재 PC에 저장된 내용 : C2]

만약, C1을 실행중인데, 요청된 인터럽트 요구에 즉시 응답
-> C1을 중단하고, ISR을 실행
-> 그러면 Stack에는 C2가 저장
-> ISR을 종료하고, CPU는 Stack의 Top에 존재하는 명령어를 꺼내서 PC에 저장
-> 이러면 PC에는 C2가 저장되고, CPU는 C2를 실행하게 된다
-> 결국, 아까 중단되었던 C1은 미처 마무리되지 못하고, C2의 수행으로 넘어가게된다

>> 따라서, 현재 실행중인 명령어는 반드시 실행 사이클을 완료하고, 그 다음에 인터럽트를 수행할지 결정해야 한다

[2.4]

인터럽트 사이클이 그림 2-9(b)와 같이 종료된 다음에 처리되는 인터럽트 서비스 루틴에서 누산기(AC)의 내용을 스택에 저장하였다. 그 값이 저장될 기억장치의 주소를 쓰고, SP의 내용은 어떤 값으로 변경되는지 쓰라.

현재 SP : 0998
-> 따라서 누산기(AC)의 내용 = 기억장치 0998번지에 저장
-> SP : 1감소 -> 0997

[2.5]

4-단계 명령어 파이프라인으로 100개의 명령어들을 모두 실행하려면 몇 클록 주기가 걸리는가? 그리고 만약 이 파이프라인의 클록 주기가 2ns라면, 그에 소요되는 전체 시간은 몇 ns인가?

T = k + (N - 1)

명령어 100개 실행
>> T = 4 + (100 - 1) = 103 클록 주기만큼 걸린다

클록 주기가 2ns
>> 전체 시간 = 103 X 2ns = 206ns

[2.6]

어떤 마이크로프로세서가 12-단계 명령어 파이프라인으로 구성되어 있고, 클록 주기는 2ns라고 하자. 10000개의 명령어를 실행하는 데 걸리는 시간과 속도 향상(Sp)을 구하라

T = {k + (N - 1)} X 클록 주기
>> {12 + (10000 - 1)} X 2ns = 20022ns

if 파이프라인 사용 X
>> T = 10000 X 12 X 2ns = 240000ns

if 파이프라인 사용 O
>> T = 20022ns

속도 향상 (Sp) = 240000ns/20022ns = 약 11.9868배

[2.7]

클록 주기가 2ns인 5-단계 명령어 파이프라인에 대하여 아래 물음에 답하라

(1) 명령어의 수 N = 10, 100 1000, 10000개를 처리하는 데 걸리는 시간을 각각 구하라

N = 10
>> T = (5 + 9) X 2ns = 28ns

N = 100
>> T = (5 + 99) X 2ns = 208ns

N = 1000
>> T = (5 + 999) X 2ns = 2008ns

N = 10000
>> T = (5 + 9999) X 2ns = 20008ns

(2) 파이프라이닝 되지 않는 경우에는 각 명령어의 실행에 걸리는 시간이 2ns X 5 = 10ns가 된다. 파이프라이닝을 이용함으로써 얻게 되는 속도 향상(Sp)을 각 N값에 대하여 구하라

N = 10
>> T = (5 + 9) X 2ns = 28ns
>> Sp = 100ns/28ns = 약 3.5714배

N = 100
>> T = (5 + 99) X 2ns = 208ns
>> Sp = 1000ns/208ns = 약 4.8077배

N = 1000
>> T = (5 + 999) X 2ns = 2008ns
>> Sp = 10000ns/2008ns = 약 4.9808배

N = 10000
>> T = (5 + 9999) X 2ns = 20008ns
>> Sp = 100000ns/20008ns = 약 4.9980배

(3) 앞 (2)번의 결과에 대한 그래프를 그려라. 단, X축은 명령어의 수 N으로 하되, log₁₀N 눈금을 사용하라

[2.8]

어떤 CPU의 명령어 파이프라인이 4개의 단계들로 이루어져 있고, 1GHz의 공통 클록이 사용되고 있다. 이 CPU가 처리할 프로그램이 100개의 명령어들로 이루어져 있는데, 그 중의 20%는 파이프라인의 두 단계만 실제 필요하고, 30%는 세 단계만 필요하며, 나머지는 4 단계 모두가 필요하다고 하자.

(1) 파이프라인을 이용하지 않은 경우에, 이 프로그램을 처리하는 데 걸리는 시간을 구하라

20%
>> 20 X 2

30%
>> 30 X 3

50%
>> 50 X 4

-> (40 + 90 + 200) X 1ns = 330ns

(2) 파이프라인을 이용하여 이 프로그램을 처리하는 데 걸리는 시간을 구하라

T = {4 + (100 - 1)} X 1ns = 103ns

(3) 파이프라이닝으로 얻어진 속도 향상(Sp)과 효율(E)을 구하라. 단, 효율은 (Sp ÷ 단계 수) X 100[%]로 구한다

Sp = 330ns/103ns = 약 3.2039배
E = (3.2039 % 4) X 100[%] = 약 80.09%

[2.9]

어떤 CPU에서 명령어 실행 과정이 네 개의 사이클들로 이루어진다고 하자. 첫 번째 사이클의 처리에 걸리는 시간이 0.5ns, 두 번째와 세 번째 사이클은 1ns 씩, 그리고 마지막 사이클은 0.75ns가 각각 걸린다고 하자.

(1) 한 명령어를 실행하는 데 걸리는 시간은?

0.5ns + 1ns + 1ns + 0.75ns = 3.25ns

(2) 각 사이클을 처리하는 하드웨어 모듈을 독립적인 파이프라인 단계로 구현한다면, 네 개의 단계들로 이루어지는 명령어 파이프라인 구조가 된다. 파이프라인의 모든 단계들은 공통의 파이프라인 클록에 동기되어 수행된다. 파이프라인 클록의 주기[ns]와 주파수[GHz]를 구하라

가장 긴 사이클의 시간이 파이프라인 클록주기의 기준 = 1ns
>> 1/(1 X 10^(-9)) = 1GHz

(3) 이 파이프라인으로 한 개의 명령어를 실행하는 데 걸리는 시간을 구하고, (1)번의 결과와 비교하라

T = 1ns X 4 = 4ns

(4) (1)번과 (3)번의 조건에서 100개의 명령어들을 실행하는 데 걸리는 시간을 각각 구하고, 파이프라이닝을 이용함으로써 얻게 되는 속도 향상(Sp)을 구하라

(1)번 조건 : T = 3.25ns X 100 = 325ns

(2)번 조건 : T = 4 + (100 - 1) = 103ns

Sp = 325ns/103ns = 약 3.1553배

[2.10]

그림 2-12와 같은 4-단계 명령어 파이프라인에서 각 단계의 실제 처리 시간이 아래와 같다고 하자. (단 ps = 10^-3ns = 10^-12sec)

IF 단계 : 500ps
ID 단계 : 400ps
OF 단계 : 500ps
EX 단계 : 450ps

(1) 파이프라인 클록의 주파수는 몇 GHz로 결정하면 되는가?

1/(500 X 10^(-12)) = 2GHz

(2) 이 파이프라인으로 100개의 명령어들을 순차적으로 실행하는데 걸리는 시간을 구하라

T = {4 + (100 - 1)} X 0.5ns = 51.5ns

(3) ALU의 속도를 향상시켜 EX 단계의 처리 시간을 400ps로 단축시킨다면, 전체 파이프라인의 성능을 높이는 데 도움이 되는가? 그 이유를 설명하라

도움이 되지 않는다
>> 가장 긴 사이클인 IF, OF의 길이가 파이프라인 클록 주기의 기준이기 때문에 EX단계의 처리 시간을 줄이는게 아니라 IF, OF단계의 처리 시간을 줄여야 전체 파이프라인의 성능이 높아진다

(4) 반대로, ALU에 새로운 기능을 추가한 결과로서 EX 단계의 처리 시간이 600ps로 길어졌다면, 파이프라인의 성능에 어떤 영향을 미치는가? 명령어 100개를 실행하는 경우에 대하여 전체 소요 시간을 계산하고, (2)번의 결과와 비교하여 설명하라

EX단계의 처리시간이 600ps가 되면 파이프라인 클록 주기가 길어지기 때문에 성능이 더 나빠진다
T = {4 + (100 - 1)} X 0.6ns = 61.8ns

(2)의 결과인 51.5ns에 비해 성능이 안좋아졌다

[2.11]

4-단계 파이프라인 단계들로 구성된 명령어 실행 유니트에서 12개의 명령어들을 처리하고자 한다. 그런데 만약 다섯 번째 명령어가 분기 명령어였다면, 분기한 후에 7개의 명령어들을 더 실행하여 모두 12개의 명령어들을 실행하는 데는 전체적으로 몇 사이클이 걸리는가?

1 ~ 5번째 : T = 4 + (5 - 1) = 8
이후 7개명령어 실행 : T = 4 + (7 - 1) = 10

>> 전체적으로 18사이클 소요

[2.12]

다섯 개의 파이프라인 단계들로 이루어진 명령어 실행 유니트가 있다.

(1) 100개의 명령어들을 실행하는 데 소요되는 시간(클록 주기의 수)을 구하라

T = 5 + (100 - 1) = 104

(2) 만약 파이프라인을 한 개 추가하여 2-way 슈퍼스칼라 구조로 변경한 경우에 100개의 명령어들을 실행하는 데 걸리는 시간을 구하고, (1)번 결과와 비교한 속도 향상을 구하라. 단 동시에 실행되는 명령어들 간에 데이터 의존성은 존재하지 않는 것으로 가정한다.

2-way 슈퍼스칼라 T = k + (N - m)/m

>> T = 5 + (100 - 2)/2 = 54

>> (1)번에 비해 약 1.9259배 성능 향상

[2.13]

네 개의 5-단계 명령어 파이프라인들로 이루어진 4-way 슈퍼스칼라 프로세서를 이용한다면, 파이프라이닝도 되지 않은 기본적인 프로세서에 비하여 최대 몇 배의 속도 향상을 얻을 수 있는가?

k-way 슈퍼스칼라 프로세서는 기본 프로세서에 비해 최대 mk배의 성능향상을 이룰 수 있다 (k = 명령어 파이프라인 단계 수, m = 슈퍼스칼라 파이프라인 수)
>> 5 X 4 = 최대 20배

[2.14]

듀얼-코어 프로세서에서 하나의 독립적인 태스크로 이루어진 응용 프로그램을 처리하는 경우에는 일반적인 프로세서에 비하여 처리 시간을 별로 단축시키지 못하는 이유를 설명하라. 그리고 듀얼-코어 및 멀티-코어 프로세서가 내부 CPU 코어 수만큼의 성능 향상을 얻을 수 있는 경우는 어떤 프로세스 처리 환경인지 설명하라

슈퍼스칼라의 명령어 파이프라인에 비해 독립성이 더 높아서 각 CPU 코어는 프로그램 실행을 독립적으로 수행하며, 필요한 경우에만 공유 캐시를 통해 정보를 교환하기 때문이다. 
응용 프로그램이 독립적으로 처리될 수 있는 여러 개(혹은 코어의 수)의 태스크 프로그램들로 분할될 수 있는 경우에 듀얼-코어 및 멀티-코어 프로세스의 내부 CPU 코어 수 만큼의 성능 향상을 얻을 수 있다.

[2.15]

16-비트 컴퓨터에서 현재 SP의 내용이 'FFF2'이고, 스택의 최상위에는 '01AB'가 저장되어 있다(모든 수는 16진수로 표기). 두 단어 길이인 서브루틴 호출(CALL) 명령어의 연산 코드가 153A 번지에, 서브루틴의 시작 주소 '2345'는 153B 번지에 각각 저장되어 있다. 아래의 각 순간에 PC와 SP의 내용을 각각 구하고, 스택에 저장되는 내용들을 그림 2-18과 같은 방법으로 표시하라

(1) CALL 명령어가 실행되기 전

	Address	Data	Memory	Address	Data	Sub-Routine
				......		프로그램
				153A	CALL opcode
				153B	2345
				......
				......
SP	FFF2			2345		서브루틴
	FFF3	01AB		......
Stack				......

CALL 명령어가 실행되기 전
>> IR : 현재 실행중인 명령어 주소 = 1539
>> PC : 다음에 실행할 명령어 주소 = 153A (서브루틴 호출 CALL 명령어)
>> SP : FFF2

:: PC = 153A / SP = FFF2

(2) CALL 명령어가 실행된 후

	Address	Data	Memory	Address	Data	Sub-Routine
				......		프로그램
				153A	CALL opcode
				153B	2345
				......
SP	FFF1			......
	FFF2	153C		2345		서브루틴
	FFF3	01AB		......
Stack				......

## CALL 명령어 실행 ##
- t(0) PC -> MBR
- t(1) SP -> MAR / X -> PC
- t(2) MBR -> M[MAR] / SP - 1 -> SP

먼저 현재 PC의 내용은 word 길이 = 2byte이기 때문에 153A + 2 = 153C이다
PC의 내용을 MBR에 저장해놓고 (MBR = 153C)
SP의 내용을 MAR에 저장해놓고 (MAR = FFF2)
서브루틴의 주소를 PC에 적재한다 (PC = 2345)
그리고 주소가 FFF2인 위치에 MBR의 내용(153C)를 적재 (M[FFF2] = 153C)
SP를 1감소시켜서 항상 스택의 최상단을 가리키게 한다 (SP = FFF1)

:: PC = 2345 / SP = FFF1

(3) 서브루틴으로부터 복귀한 후

	Address	Data	Memory	Address	Data	Sub-Routine
				01AB
				......
				......		프로그램
				153A	CALL opcode
				153B	2345
				153C
				......
SP	FFF2			2345		서브루틴
	FFF3	01AB		......
Stack				......

## RET 명령어 실행 ##
- t(0) SP + 1 -> SP
- t(1) SP -> MAR
- t(2) M[MAR] -> PC

먼저 SP를 1증가시켜서 마지막에 저장해놓은 복귀 주소를 가리키게 한다 (SP = FFF2)
그 다음에 SP를 MAR에 저장해놓고 (MAR = FFF2)
주소가 FFF2인 위치의 Data(복귀 주소)를 PC에 적재 (PC = 153C)

:: PC = 153C / SP = FFF2

(4) 다시 한 번 RET 명령어가 실행된 후

	Address	Data	Memory	Address	Data	Sub-Routine
				01AB
				......
				......		프로그램
				153A	CALL opcode
				153B	2345
				153C
				......
				2345		서브루틴
SP	FFF3			......
Stack				......

## RET 명령어 실행 ##
- t(0) SP + 1 -> SP
- t(1) SP -> MAR
- t(2) M[MAR] -> PC

먼저 SP를 1증가시켜서 마지막에 저장해놓은 복귀 주소를 가리키게 한다 (SP = FFF3)
그 다음에 SP를 MAR에 저장해놓고 (MAR = FFF3)
주소가 FFF3인 위치의 Data(복귀 주소)를 PC에 적재 (PC = 01AB)

:: PC = 01AB / SP = FFF3

[2.16]

다음 수식을 계산하기 위한 프로그램을 아래의 명령어들을 사용하여 작성하고, 프로그램의 길이를 비교하라. (단, 명령어들의 니모닉스는 2.4.2절을 참조)

X = (A + B) / (D - E X F + G X H)

(1) 1-주소 명령어

중간에 계산결과를 임시로 저장할 기억장치 T, P, V, W

1. LOAD A

M[A] -> AC
▶ 기억장치 A의 내용을 AC에 저장

AC >> A

2. ADD B

AC + M[B] -> AC
▶ AC의 내용(A)과 기억장치 B의 내용을 더해서 AC에 저장

AC >> A + B

3. STOR T

AC -> M[T]
▶ AC의 내용(A+B)을 임시 기억장치 T에 저장

T >> A + B

4. LOAD E

M[E] -> AC
▶ 기억장치 E의 내용을 AC에 저장

T >> A + B
------------------
AC >> E

5. MUL F

AC × M[F] -> AC
▶ AC의 내용(E)과 기억장치 F의 내용을 곱해서 AC에 저장

T >> A + B
------------------
AC >> E × F

6. STOR P

AC -> M[P]
▶ AC의 내용(E × F)을 임시 기억장치 P에 저장

T >> A + B
P >> E × F

7. LOAD G

M[G] -> AC
▶ 기억장치 G의 내용을 AC에 저장

T >> A + B
P >> E × F
-------------
AC >> G

8. MUL H

AC × M[H] -> AC
▶ AC의 내용(G)과 기억장치 H의 내용을 곱해서 AC에 저장

T >> A + B
P >> E × F
-------------
AC >> G × H

9. STOR V

AC -> M[V]
▶ AC의 내용(G × H)을 임시 기억장치 V에 저장

T >> A + B
P >> E × F
V >> G × H

10. LOAD D

M[D] -> AC
▶ 기억장치 D의 내용을 AC에 저장

T >> A + B
P >> E × F
V >> G × H
------------
AC >> D

11. SUB P

AC - M[P] -> AC
▶ AC의 내용(D)과 기억장치 P의 내용(E × F)을 빼서 AC에 저장

T >> A + B
V >> G × H
------------
AC >> D - E × F

12. ADD V

AC + M[V] -> AC
▶ AC의 내용(D - E × F)과 기억장치 V의 내용(G × H)를 더해서 AC에 저장

T >> A + B
------------
AC >> D - E × F + G × H

13. STOR W

AC -> M[W]
▶ AC의 내용(D - E × F + G × H)을 임시 기억장치 W에 저장

T >> A + B
W >> D - E × F + G × H

14. LOAD T

M[T] -> AC
▶ 기억장치 T(A+B)의 내용을 AC에 저장

W >> D - E × F + G × H
------------------------
AC >> A + B

15. DIV W

AC / M[W] -> AC
▶ AC의 내용(A+B)을 기억장치 W의 내용(D - E × F + G × H)으로 나눠서 AC에 저장

AC >> (A + B) / D - E × F + G × H

16. STOR X

AC -> M[X]
▶ AC의 내용{(A + B) / (D - E × F + G × H)}을 기억장치 X에 저장

X >> (A + B) / (D - E × F + G × H)

(2) 2-주소 명령어

연산 코드 + R1 + R2 (레지스터 R1, 레지스터 R2)

1. MOV R2, E

M[E] -> R2
▶ 기억장치 E의 내용을 R2에 저장

R2 >> E

2. MUL R2, F

R2 × M[F] -> R2
▶ R2의 내용(E)과 기억장치 F의 내용을 곱해서 R2에 저장

R2 >> E × F

3. MOV R1, G

M[G] -> R1
▶ 기억장치 G의 내용을 R1에 저장

R2 >> E × F
------------
R1 >> G

4. MUL R1, H

R1 × M[H] -> R1
▶ R1의 내용(G)과 기억장치 H의 내용을 곱해서 R1에 저장

R2 >> E × F
-------------
R1 >> G × H

5. ADD R2, R1

R2 + R1 -> R2
▶ R2의 내용(E × F)과 R1의 내용(G × H)을 더해서 R2에 저장

R2 >> E × F + G × H

6. MOV R1, D

M[D] -> R1
▶ 기억장치 D의 내용을 R1에 저장

R2 >> E × F + G × H
----------------------
R1 >> D

7. SUB R1, R2

R1 - R2 -> R1
▶ R1의 내용(D)과 R2의 내용(E × F + G × H)을 빼서 R1에 저장

R1 >> D - E × F + G × H

8. MOV R2, R1

R1 -> R2
▶ R1의 내용(D - E × F + G × H)를 R2에 저장

R2 >> D - E × F + G × H

9. MOV R1, A

M[A] -> R1
▶ 기억장치 A의 내용을 R1에 저장

R2 >> D - E × F + G × H
--------------------------
R1 >> A

10. ADD R1, B

R1 + M[B] -> R1
▶ R1의 내용(A)과 기억장치 B의 내용을 더해서 R1에 저장

R2 >> D - E × F + G × H
--------------------------
R1 >> A + B

11. DIV R1, R2

R1 / R2 -> R1
▶ R1의 내용(A + B)과 R2의 내용(D - E × F + G × H)을 나눠서 R1에 저장

R1 >> (A + B) / D - E × F + G × H

12. MOV X, R1

R1 -> X
▶ R1의 내용{(A + B) / (D - E × F + G × H)}을 X에 저장

X >> (A + B) / (D - E × F + G × H)

(3) 3-주소 명령어

1. MUL R2, E, F

M[E] × M[F] -> R2
▶ 기억장치 E의 내용과 기억장치 F의 내용을 곱해서 R2에 저장

R2 >> E × F

2. MUL R1, G, H

M[G] × M[H] -> R1
▶ 기억장치 G의 내용과 기억장치 H의 내용을 곱해서 R1에 저장

R1 >> G × H

3. ADD R2, R2, R1

R2 + R1 -> R2
▶ R2의 내용(E × F)와 R1의 내용(G × H)를 더해서 R2에 저장

R2 >> E × F + G × H

4. SUB R2, D, R2

M[D] - R2 -> R2
▶ 기억장치 D의 내용과 R2의 내용(E × F + G × H)를 빼서 R2에 저장

R2 >> D - E × F + G × H

5. ADD R1, A, B

M[A] + M[B] -> R1
▶ 기억장치 A의 내용과 기억장치 B의 내용을 더해서 R1에 저장

R2 >> D - E × F + G × H
------------------------
R1 >> A + B

6. DIV X, R1, R2

R1 / R2 -> X
▶ R1의 내용(A + B)과 R2의 내용(D - E × F + G × H)를 나눠서 기억장치 X에 저장

X >> (A + B) / (D - E × F + G × H)

※ 최종 프로그램 길이 비교

1-주소 명령어 : 16
2-주소 명령어 : 12
3-주소 명령어 : 6

[2.17]

스택을 이용한 연산이 가능한 CPU가 있다고 하자. 이 CPU에서 'PUSH A'명령어는 기억장치 A번지의 내용을 읽어서 스택의 최상위(TOS)에 저장하며, 'POP B'명령어는 TOS의 내용을 인출하여 기억장치 B번지에 저장한다. 또한 산술 명령어들은 오퍼랜드를 가지지 않는 0-주소 명령어이다. 예를 들어, ADD 명령어는 그림 2-35와 같이 TOS와 그 아래에 있는 2개의 데이터들을 더하고, 결과값은 다시 TOS에 저장한다. 스택 명령어들(PUSH, POP)과 0-주소 산술 명령어들(ADD, SUB, MUL)을 이용하여 아래의 수식을 계산하는 프로그램을 작성하라

X = (A + B) * (C - D)

1. PUSH A

기억장치 A의 내용을 스택에 PUSH

Stack



SP→	A

2. PUSH B

기억장치 B의 내용을 스택에 PUSH

Stack


SP→	B
	A

3. ADD

스택 위의 값 2개(A, B)를 POP해서 더하고 다시 스택에 PUSH

Stack



SP→	A + B

4. PUSH C

기억장치 C의 내용을 스택에 PUSH

Stack


SP→	C
	A + B

5. PUSH D

기억장치 D의 내용을 스택에 PUSH

Stack

SP→	D
	C
	A + B

6. SUB

스택 위의 값 2개(C, D)를 POP해서 빼고 다시 스택에 PUSH

Stack


SP→	C - D
	A + B

7. MUL

스택 위의 값 2개(A+B, C-D)를 POP해서 곱하고 다시 스택에 PUSH

Stack



SP→	(A + B) × (C - D)

8. POP X

스택에서 POP한 값((A+B) × (C-D))를 기억장치 X에 저장

[2.18]

문제 2.17에서와 같은 스택 연산에 대하여 다음과 같은 reverse Polish(후위 표기)가 사용될 수 있다.

a+b -> ab+
a+(b*c) -> abc*+
(a-b)*c -> ab-c*

아래 식들을 reverse Polish 표기를 사용하여 변환하라

import java.util.*;
public class Main{
    static Scanner sc = new Scanner(System.in);
    public static void main(String[] args) {
        while(true){
            String line = sc.nextLine();
            if(line.equals("exit"))
                break;
            postfix(line);
        }
    }

    static int priority(char op){
        // 연산자 우선순위
        switch(op){
            case '(': case ')':
                return 1;
            case '+': case '-':
                return 2;
            case '*': case '/':
                return 3;
        }
        return -1;
        // 스택에 우선순위가 낮은게 들어오려고하면 스택에 존재하는 우선순위 더 높은거를 pop하고 push
    }

    static void postfix(String line){
        Stack<Character> s = new Stack<>();

        for(int i=0; i<line.length(); i++){
            char [] c = line.toCharArray();
            switch(c[i]){
                case '+': case '-': case '*': case'/':
                    while(!s.isEmpty() && (priority(s.peek()) >= priority(c[i])))
                        System.out.print(s.pop());
                    s.push(c[i]);
                    break;
                case '(':
                    s.push(c[i]);
                    break;
                case ')':
                    char top = s.pop();
                    while(top != '('){
                        System.out.print(top);
                        top = s.pop();
                    }
                    break;
                default: // 피연산자는 그냥 출력
                    System.out.print(c[i]);
                    break;
            }
        }
        while(!s.isEmpty())
            System.out.print(s.pop());
        System.out.println("\n");
    }
}

(1) A+B-C-D-E

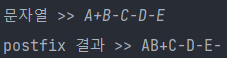
**(2) (A+B)*(C-D)+E**

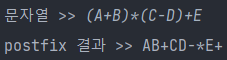
**(3) (AB)+(CD)-E**

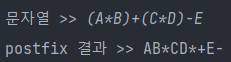
**(4) (A-B)(((C-DE)/F)/G)*E**

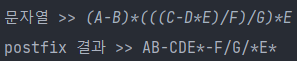
[2.19]

16-비트 명령어에서 6비트가 연산 코드로 사용되고, 나머지 비트들은 2의 보수로 표현되는 데이터를 저장하는 오퍼랜드 필드이다. 이 명령어에 저장될 수 있는 데이터의 범위를 구하라

Operand 필드 비트 수 = 10bit
>> 데이터 표현 범위 = -2^(10-1) ~ 2^(10-1) - 1 = -512 ~ 511

[2.20]

32-비트 CPU가 128가지의 연산들을 수행하며, 내부 레지스터의 수는 32개라고 하자. 이 CPU의 명령어 형식은 연산 코드 필드와 레지스터 번호를 나타내는 오퍼랜드1 및 나머지 비트들로 구성되는 주소 필드(오퍼랜드2)로 이루어진다.

(1) 명령어 형식을 표시하라

Op Code	Operan1 (Register)	Operand2 (Address)
7bit	5bit	20bit

Op Code
>> 128가지 연산 수행
>> 2^(7) = 128
>> 7bit

Operand 1 (Register)
>> 내부 레지스터 수 = 32개 = 2^(5)
>> 5bit

Operand 2 (Address)
>> 32-bit CPU
>> 32 - 7 - 5 = 20bit

(2) 이 명령어에 의해 직접 주소지정 될 수 있는 기억장치의 용량을 구하라. 단, 기억장치 주소는 byte 단위로 지정된다고 가정하자.

주소 필드 비트 수 = 20bit
>> 기억장치 용량 = 2^(20)byte

[2.21]

아래와 같은 주소지정 방식을 사용하는 명령어를 인출하고 실행하기 위해서는 모두 몇 번의 기억장치 엑세스가 필요한가?

(1) 즉시 주소지정 방식

- Operand 내용이 실제 Data이기 때문에 기억장치에 액세스할 필요가 없다

>> 0번

(2) 레지스터 주소지정 방식

EA = R
- Operand의 내용이 Register이고, 해당 Register의 내용이 실제 Data이기 때문에, 기억장치에 액세스할 필요가 업다

>> 0번

(3) 간접 주소지정 방식

EA = (A)
- Operand의 내용(주소 A)의 주소가 실제 Data의 유효주소이기 때문에 기억장치에 2번 액세스 해야 한다

>> 2번

(4) 인덱스 주소지정 방식

EA = A + (IR)
- IR의 내용 + 주소 A가 실제 Data의 유효주소이므로 기억장치에 1번만 액세스하면 된다

>> 1번

[2.22]

32-비트 컴퓨터에서 명령어가 지정할 수 있는 연산의 종류를 256가지로 결정하고, 직접 주소지정 방식을 사용하는 경우에, 시스템이 가질 수 있는 기억장치의 최대 용량을 구하라. 단, 기억장치의 주소는 byte 단위로 지정된다

직접 주소지정 방식 : OpCode + Operand
>> Opcode = 연산의 종류 = 256 = 2^(8) = 8bit
>> 따라서 남은 24bit가 Operand 필드의 비트 수이다

>> 최대 기억장치 용량 = 2^(24)byte

[2.23]

프로그램 카운터의 내용을 X1이라 하고, 기억장치 X1번지에 저장된 명령어의 주소 부분을 X2라고 하자. 그 명령어를 실행하는 데 필요한 데이터는 기억장치 X3번지에 저장되어 있으며, 인덱스 레지스터의 내용은 X4이다. 명령어가 아래와 같은 주소지정 방식을 사용하는 경우에 유효 주소(EA)에 대한 관계식을 변수들을 이용하여 쓰라

명령어
- Opcode : ~~~~
- Operand : X2

(PC) = X1
(X2) = X3
(IX) = X4

(1) 직접 주소지정 방식

EA = A

>> EA = X2

(2) 간접 주소지정 방식

EA = (A)

>> EA = X3

(3) 상대 주소지정 방식

EA = A + (PC)

>> EA = X2 + X1