2022. 2. 2. 19:29ㆍSolution`/컴퓨터구조론
[3.1]
2의 보수 표현이 1의 보수 표현보다 더 널리 사용되고 있는 주요 이유는 무엇인가?
1. 산술 연산이 더 편리하다
2. 음수 표현이 가능하다
3. 10진수 변환이 더 용이하다
4. 표현할 수 있는 수의 개수가 하나 더 많다
1의 보수는 0을 표현하는 방법이 2가지
>> 2의 보수로 표현할 수 있는 수의 개수 = 1의 보수로 표현할 수 있는 수의 개수 + 1
[3.2]
10진수 '-75'에 대한 2의 보수 표현으로 올바른 것은 어느 것인가?
1. 11001011
2. 10110101
3. 10110100
4. 11001010
75 : 01001011
>> 1의 보수 : 10110100
>> 2의 보수 : 1의 보수 + 1 = 10110101
[3.3]
2의 보수 '11101000'을 10진수로 변환하면 어떤 값이 되는가?
1. -12
2. 48
3. -24
4. 232
방법 1)
-128 + (64 + 32 + 8) = -24
방법 2) 2의 보수 방법을 역으로 이용
11101000
>> 1의 보수 : 00010111
>> 1더하기 : 00011000 = 24
>> - 붙여주기 : -24
[3.4]
특정 비트들을 마스크(mask) 시키기 위하여 사용되는 논리 연산은 무엇인가?
1. AND 연산
2. OR 연산
3. XOR 연산
4. NOT 연산
마스크 연산 : 특정 bit들을 0으로 만들어주기 위해 수행하는 연산
>> B 레지스터 : 0으로 만들고 싶은 bit들을 0으로 설정 / 나머지는 1로 설정
>> A, B의 AND 연산을 통해 특정 bit들을 0으로 만들기
[3.5]
두 수를 비교하기 위하여 사용되는 논리 연산은 무엇인가?
1. AND 연산
2. OR 연산
3. XOR 연산
4. NOT 연산
두 레지스터의 bit들을 비교
>> bit가 같으면 A레지스터의 해당 bit를 0으로 설정
>> XOR 연산을 통해서 수행
[3.6]
A 레지스터에 '01101010'이 저장되어 있는 상태에서 B 레지스터와의 XOR 연산을 이용하여 상위 다섯 비트를 보수값으로 바꾸고자 한다. 레지스터 B에는 어떤 값을 넣어야 하는가?
1. 00000111
2. 11111000
2. 00001111
4. 11110000
특정 bit들을 보수값으로 변경 : 선택적-보수 연산
>> B 레지스터 : 보수값으로 변경할 bit들을 1로 설정 / 나머지 bit들은 0으로 설정
A 레지스터 : 01011011 >> 상위 다섯 비트를 보수값으로 변경
B 레지스터 : 11111000
[3.7]
A 레지스터에 2의 보수로 표현된 데이터 '10101101'이 저장되어 있을 때, 산술적 우측 시프트를 2번 수행한 결과는 다음 중 어느 것인가?
1. 00101011
2. 01010110
3. 11010110
4. 11101011
산술적 우측-시프트 : 부호 비트는 무조건 고정
(1) 10101101 >> 최상위 비트(부호 비트) 1은 시프트와 상관없이 무조건 고정
(2) 11010110
(3) 11101011 - result
[3.8]
A 레지스터에 '01011011'이 저장되어 있을 때, 좌측 순환 시프트를 1번 수행한 결과는 다음 중 어느 것인가?
1. 10101101
2. 10110110
3. 10110111
4. 00101101
좌측 순환 시프트 : 최상위 bit를 최하위 bit로 옮기고 나머지 bit들은 왼쪽으로 1칸씩 옮기기
01011011 >> 10110110
[3.9]
A 레지스터에 '01011011'이 저장되어 있고 C 플래그에 '1'이 저장되어 있을 때, SHRC 연산을 1번 수행한 결과는 다음 중 어느 것인가?
1. 00101101
2. 10101101
3. 10110111
4. 10110110
SHRC : 최상위 bit를 C플래그 값으로 설정하고 나머지 bit들은 오른쪽으로 1칸씩 이동
C(1), 01011011 >> 10101101
[3.10]
A 레지스터에 '01011011'이 저장되어 있고 C 플래그에 '0'이 저장되어 있을 때, RLC 연산을 2번 수행한 결과는 다음 중 어느 것인가?
1. 10101101
2. 00101101
3. 01101100
4. 10110110
RLC : 최하위 bit는 C플래그 값으로 설정하고, 나머지 bit들은 왼쪽으로 1칸씩 이동, 최상위bit의 값은 C플래그에 저장
C(0), 01011011
RLC 연산 수행 : C(0) 10110110
RLC 연산 수행 : C(1) 01101100
[3.11]
아래의 2의 보수 덧셈들 중에서 오버플로우가 발생하는 것은?
1. 0010 + 0110
2. 0100 + 0011
3. 1110 + 1010
4. 0011 + 1010
| 수식 | 연산 과정 | 오버플로우 판별 |
| 1. 0010 + 0110 |  |
C1 : 1 C2 : 0 >> 오버플로우 O |
| 2. 0100 + 0011 | 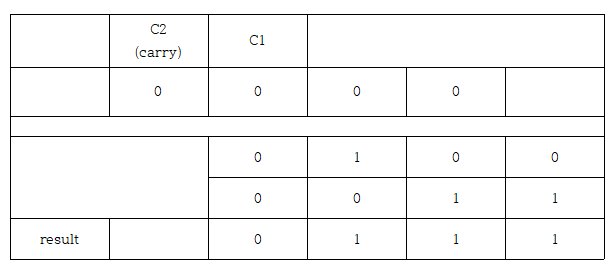 |
C1 : 0 C2 : 0 >> 오버플로우 X |
| 3. 1110 + 1010 |  |
C1 : 1 C2 : 1 >> 오버플로우 X |
| 4. 0011 + 1010 | 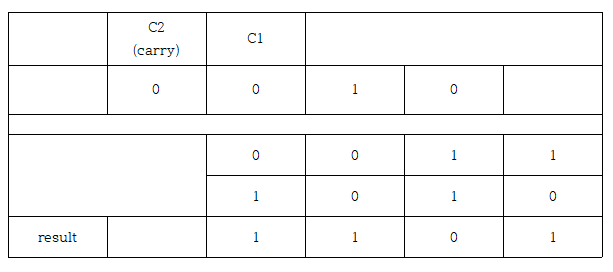 |
C1 : 0 C2 : 0 >> 오버플로우 X |
[3.12]
다음 중에서 정규화된 표현은 어느 것인가?
1. 0.001011 × 27
2. 0.101100 × 25
3. 1.011000 × 24
4. 1011.00 × 21
[3.13]
2진수 0.1011×25을 IEEE 754 표준 부동소수점 형식으로 표현하면, 가수(mantissa)의 처음 다섯 비트는 어떤 값이 되는가?
1. 10110
2. 01100
3. 00110
4. 01011
IEEE 754 표준 부동소수점 형식 : 바이어스 = 127 / 가수 필드 = 부동소수점 형식
0.1011 X 2^(5) --> 1.011 X 2^(4)
지수 필드 = 4 + 127 = 0000 0100 + 0111 1111 = 1000 0011
가수 필드 = 011 0000 0000 0000 0000 0000
[3.14]
2진수 0.1011×25을 IEEE 754 표준 부동소수점 형식으로 표현하면, 지수(exponent)는 어떤 값이 되는가?
1. 10000100
2. 10000101
3. 10000011
4. 00000100
IEEE 754 표준 부동소수점 형식 : 바이어스 = 127 / 가수 필드 = 부동소수점 형식
0.1011 X 2^(5) --> 1.011 X 2^(4)
지수 필드 = 4 + 127 = 0000 0100 + 0111 1111 = 1000 0011
가수 필드 = 011 0000 0000 0000 0000 0000
[3.15]
다음 중 부동소수점 덧셈 과정에서 필요하지 않은 연산은 어느 것인가?
1. 지수 조정
2. 정규화
3. 지수 덧셈
4. 가수 덧셈
[3.16]
다음 중 부동소수점 나눗셈 과정에서 필요하지 않은 연산은 어느 것인가?
1. 지수 조정
2. 정규화
3. 가수 나누기
4. 지수 뺄셈
