2022. 6. 4. 18:01ㆍMajor`/정보보호개론
네트워크 측면에서 프로토콜은 연결된 다양한 통신시스템이 준수해야 할 규칙이다.
여기서는 "인증"을 목적으로 네트워크를 통해 전송되는 메시지에 대한 보안 문제를 다룰 것이다.
네트워크를 통해 전송되는 메시지에 대한 공격은 크게 {Replay Attack & MITM Attack}로 분류할 수 있다
단순 보안 프로토콜
1) 미 국가보안국 (NSA)의 출입증 & PIN
NSA에 들어가려면 직원은 항상 출입증을 가지고 있어야 한다
그리고 어떤 gate에 출입증을 제시함과 동시에 자신이 알고있는 PIN을 입력해야 한다
1. 출입증을 판독기에 넣기
2. PIN 번호 입력
>> PIN번호가 유효하면 건물에 들어가고, 유효하지 않으면 총에 맞아 죽는다
2) ATM에서 현금 인출
1. 현금카드를 판독기에 넣기
2. PIN 번호 입력
>> 유효하면 현금 인출하고, 유효하지 않으면 카드 압수당한다
3) 군의 특수 프로토콜 : 피아식별(IFF : Identity Friend or Foe)
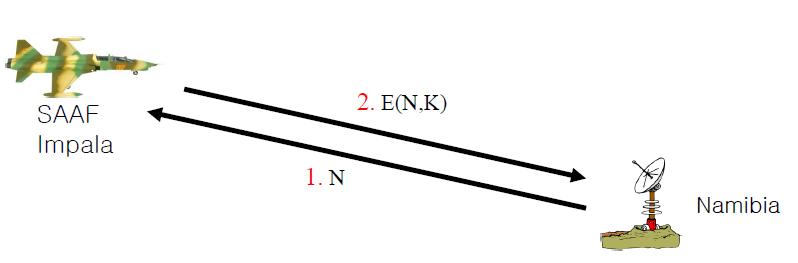
1. 레이더기지에서는 레이더로 전투기가 포착되면 Nonce를 전투기에 보냄에 따라 "이 문제를 풀어서 나한테 다시 넘겨라"라고 요구한다
2. 전투기는 Nonce를 받으면 {레이더 & 전투기}가 공유하고 있는 key를 통해서 Nonce를 암호화한 후 암호화 값을 레이더 기지로 보낸다
3. 레이더 기지는 공유하고 있는 key를 통해서 잘 암호화해서 보냈나 확인하고, 정확하게 보냈으면 아군임을 인지한다


여기서 러시아 미그기가 "SAAF측 레이더 기지망"에 접근을 해서 공격을 시도하려고 한다
당연히 레이더기지는 Nonce를 보내서 "우리가 아군이라면 공유하는 키를 너도 알것이고 따라서 암호화해서 결과를 보내라"라고 요구할 것이다
하지만 여기서 SAAF 전투기도 "러시아측 레이더 기지망인 Angloa"를 공격하려는 임무를 시도중이었다고 하자
러시아 미그기는 "SAAF측 레이더 기지"로부터 받은 Nonce를 암호화한 값 E(N, K)를 빨리 응답해야 한다. 응답하지 않으면 죽는다
근데 러시아 미그기는 암호화할 때 필요한 K를 알 수가 없다 (아군이 아니기 때문에)
그래서 "러시아측 레이더 기지"인 Angloa에게 본인이 받은 Nonce값을 보낸다
그리고 Angola는 SAAF 전투기에게 Nonce를 똑같이 보내서 러시아 미그기가 원하는 값인 E(N, K)를 받을 수 있었다
따라서 러시아 미그기는 최종적으로 "SAAF측 레이더 기지"가 원하는 답인 E(N, K)를 얻을 수 있고 그에 따라서 "SAAF측 레이더 기지"는 러시아 미그기에게 공격을 받게 된다
>> 이렇게 중간에서 어떠한 값을 중계해서 가하는 공격을 MITM Attack이라고 한다
인증 프로토콜
인증에는 단방향 인증이 있고 양방향 인증이 존재한다
단방향 인증의 경우 A가 B한테 인증을 하면 B는 A를 알지만 A는 B를 모르는 경우를 단방향 인증이라고 한다
양방향 인증은 A가 B한테 인증을해서 B가 A를 알면, B도 A한테 인증을 해서 A가 B를 아는 경우를 양방향 인증이라고 한다
(1) 가장 단순한 인증 프로토콜

보면 Alice는 먼저 Bob에게 "나는 Alice"라고 인증을 시도하고, Bob은 Alice가 맞는지 증명해보라고 한다
그러자 Alice는 자신의 비밀번호를 인증 수단으로 사용해서 Bob에게 인증을 하였다
이것은 Alice가 Bob에게 인증을 하고 Bob은 Alice에게 인증을 하지 않은 "단방향 인증"이다
이러한 인증 프로토콜은 굉장히 심각한 결함을 내포하고 있다
"Trudy"입장에서는 저 메시지들을 전부 관찰할 수 있고, 그에 따라서 Trudy는 Alice인 척 Bob에게 인증을 할 수 있다


이러한 Trudy의 공격 방법을 "Replay Attack"이라고 한다
(2) 좀 더 나은 인증 프로토콜
이것을 깨달은 Alice는 아까보다는 더 나은 인증 프로토콜로 인증을 시도하였다
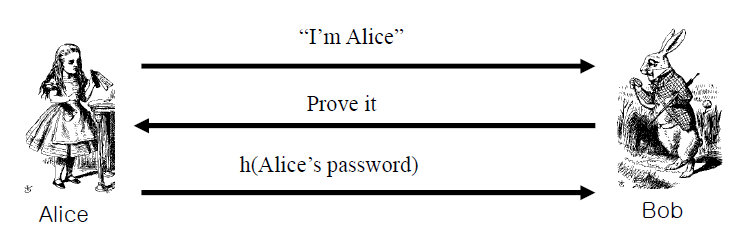
아까는 비밀번호를 그대로 보냈지만 지금은 비밀번호를 Hasing해서 보내었다
그러면 이러한 인증 프로토콜은 "Replay Attack"을 막을 수 있을까??

Trudy는 Alice의 정확한 비밀번호를 모르지만, 비밀번호를 Hashing한 값은 알 수 있기 때문에 Hashing한 값 그대로 Alice인척 Bob에게 전달하면 인증이 완료된다
여기서도 Replay Attack이 성공적으로 된 것을 확인할 수 있다
그러면 이러한 Replay Attack은 영원히 막을 수 없을까??
>> "Nonce"를 활용하면 Replay Attack을 막을 수 있다
(3) Nonce를 활용한 인증 프로토콜
질문 & 응답구조를 통해서 인증 프로토콜을 새로 생성해내었다

Alice는 마찬가지로 Bob에게 "나는 Alice"야 라고 인증을 요청했다
그러자 Bob은 "Nonce"를 생성해서 "Alice야 이 Nonce를 통해서 내 질문을 해결해봐라"라고 요구하였다
- 질문에 대한 응답은 Alice만 생성해낼 수 있어야 하고, Bob은 확인할 수 있어야 한다
그러자 Alice는 {본인의 비밀번호 + Nonce}를 Hashing한 값을 Bob에게 전달하였다
이 후 Bob은 Alice에 대한 인증을 완료하였다
그러면 여기서는 Trudy가 Replay Attack을 하지 못할까????
>> 하지 못한다

왜냐하면 Nonce는 매번 새로 생성되는 Random한 값이므로 이전에 H(password, nonce)를 볼 수 있더라고 이후에 nonce는 다른 값이므로 저 hashing된 값은 더이상 유효한 값이 아니다
따라서 Nonce를 통해서 Replay Attack을 막을 수 있다는 것을 알게 되었다
대칭키 인증
이전에 Hash가 유효한 것으로 판명났기 때문에 다른 형태의 암호화도 유용할 것이라고 생각할 수 있다
Alice & Bob은 대칭키 K(ab)를 공유하고 있으며 이 대칭키는 오직 Alice & Bob만 알고 있다고 하자
그리고 서로 인증하는 과정에서 Trudy에게 이 대칭키를 노출하면 안되고, Replay Attack도 막아야 한다
(1) Version 1
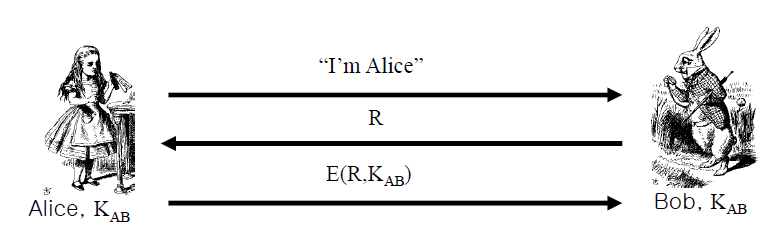
이전에는 Nonce를 받으면 비밀번호와 함께 Hashing해서 전달하였다
하지만 여기서는 Nonce를 받으면 서로가 공유하는 "대칭키"를 활용해서 "Nonce를 대칭키로 암호화한 결과"를 Bob에게 전달한다
이러한 인증 프로토콜은 대칭키를 서로만 알고있기 때문에 Replay Attack을 막을 수 있다(Nonce는 매번 새롭기 때문에)
하지만 "상호인증"이 결여된 것을 볼 수 있다
(2) Version 1 + "상호인증"

이것은 딱 봐도 문제가 뭔지 알 수 있다
Alice의 3번째 답변은 Bob의 2번째 답변과 일치한다
Alice쪽에 Trudy가 서있어도 그냥 응답받은 결과 그대로 재응답하면 Bob은 그거를 받게 된다
따라서 Bob은 Alice인지 Trudy인지 인증조차 하지 못하는 문제가 발생한다

위의 동일성 문제를 해결하기 위한 프로토콜을 만들어봤다
1. Alice는 "나는 Alice"야 라고 보냄과 동시에 "Bob을 인증할 수 있는 Nonce"도 같이 보내었다
2. Bob은 Alice가 보낸 Nonce에 대해서 서로 공유하는 대칭키를 이용해서 암호화한 결과를 보낸다. 그리고 동시에 "Alice를 인증할 수 있는 또 다른 Nonce"도 같이 보낸다
3. Alice는 Bob이 보낸 Nonce에 대해서 서로 공유하는 대칭키를 이용해서 암호화한 결과를 보낸다
언뜻 보면 상호인증이 완벽하게 되었다고 생각할 수 있다

Trudy는 Alice인척하면서 Bob에게 "나는 Alice야"라고 함과 동시에 Nonce를 생성해서 Bob에게 보낸다
Bob은 Alice로부터 Nonce를 받은걸로 착각하고 "Alice & Bob이 공유하는 대칭키"를 활용해서 받은 Nonce를 암호화해서 Trudy에게 보낸다. 그리고 Bob도 상대방이 누군지 인증하기 위해서 Nonce를 생성해서 보낸다
여기서 Trudy는 "Alice & Bob이 공유하는 대칭키"를 모르기 때문에 Bob이 보낸 Nonce에 대해서 암호화를 할 수 없다
>> 여기서 Trudy는 꾀를 부린다
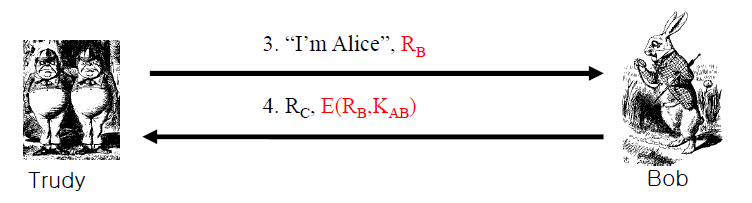
결국 Trudy는 대칭키를 몰라서 E(R(b), K(ab))를 구할 수 없기 때문에 본인이 받은 Nonce인 R(b)를 Bob에게 새로 접속한척하고 보내게 된다
그리고 Bob은 Nonce R(b)를 받았기 때문에 그거를 "Alice & Bob이 공유하는 대칭키"를 통해서 암호화한 결과를 응답한다
>> 여기서 최종적으로 Trudy가 원하는 값이니 E(R(b), K(ab))를 Bob으로부터 받게 되었다

이제 원하는 값을 얻게 되었으니까 아까 중단했던 프로토콜을 다시 재개함으로써 Trudy는 Bob에게 응답할 수 있게 되었다. 따라서 Trudy는 Alice인척 인증을 완료했다
>> 이러한 공격방법을 Reflection Attack이라고 한다
따라서 위에서 성공했던 단방향성 인증 프로토콜은 상호인증에 대해서는 안전하지 않을 수 있다
(3) 공개키 인증 프로토콜 최종 Version

위에서는 암호화를 할 때 {Nonce + 공유 키}만을 넣어서 암호화했지만 여기서는 {"본인의 신분" + Nonce + 공유 키}를 넣어서 암호화 하였다
따라서 이 경우 Trudy가 중간에서 공격을 하려고 해도 Trudy가 받은 값은 E("Bob", R, K)인데 Trudy가 응답해야 할 값은 E("Alice", R, K)이다
이 결과는 알수가 없기 때문에 MITM Attack이 소용이 없다
공개키 인증
위에서 대칭키를 통한 안전한 상호인증 프로토콜을 만들 수 있었다
그러면 이제 공개키를 통한 안전한 상호인증 프로토콜을 만들어보자

상대방의 공개키를 통해서 암호화하는 것은 그냥 암호화라고 하고, 본인의 "Private Key"를 통해서 암호화하는 것을 "전자서명"이라고 한다
전자서명은 부인봉쇄 기능을 더해줄 수 있다
<A입장에서>
1. B에게 B의 공개키를 통해서 암호화한 결과를 보냄
>> B는 본인의 private key(B's private key)를 통해서 복호화 가능
2. B에게 자신의 private key(A's private key)를 통해서 서명한 결과를 보냄
>> B는 A의 공개키를 통해서 복호화 가능
(1) Version 1 (암호화)

Alice는 Bob에게 "나는 Alice야"라고 인증 요청을 보냈다
Bob은 Nonce값을 하나 생성해서 이 Nonce값을 "Alice's 공개키"를 통해서 암호화해서 Alice에게 보내었다
>> 이것은 Alice의 Private key로만 복호화 가능
Alice는 본인이 공개키로 암호화한 암호문을 받아서 본인의 Private Key로 복호화한 결과 : R을 Bob에게 보냄으로써 인증을 하였다
그런데 여기서는 심각한 결함이 하나 존재한다
Trudy는 둘간의 여러 메시지를 도청했다고 하자.
하지만 Alice의 private key를 모르기 때문에 메시지 내용은 알 수 없다
여기서 Trudy는 메시지를 알고 싶어서 둘간의 프로토콜 사이에 몰래 Bob인척 잠입을 한다
그리고 Trudy는 Alice에게 {R}Alice대신 {<이전에 도청한 메시지>}Alice를 보내게 된다
그러면 Alice는 본인의 private key를 이용해서 복호화해서 Trudy에게 전달해주고 Trudy는 이전에 도청한 메시지가 뭔지 알 수 있게 되었다
(2) Version 2 (서명)

이렇게 서명을 통한 인증은 딱봐도 문제가 많아보인다
왜냐하면 Trudy가 Bob인척하고 아무거나 보내면 Alice는 그에 대한 "서명"을 보내기 때문에 Trudy는 "Alice의 자필서명"을 악용할 수 있다
일반적으로 {암호화 & 서명}을 할 때 동일한 키 쌍을 사용하는 것은 굉장히 보안적으로 좋지 않은 행위이다
따라서 {암호화/복호화}와 {서명/인증}할 때의 key를 서로 다르게 사용해야 한다
그리고 더불어서 인증을 할 때도 위의 2가지 Case와 전혀 다른 key를 사용해야 한다
세션 키
세션이란 user간의 대화의 생명주기?라고 볼 수 있다
임시로 만들어지는 세션 내에서 데이터가 교환될 때 데이터에 대한 비밀성 & 무결성을 보장해주는 것이 "세션 키"이다
세션 키도 세션이 만들어질 때 임시로 생성되고, 세션이 종료될때 세션 키도 사라진다
- 보통 세션키는 "대칭키" 형태로 만들어진다
- 대규모 데이터를 암호화/복호화할때는 성능이 중요하기 때문에 대칭키를 이용한다
세션키가 추가된 프로토콜은 {이 세션키를 공격자에게 노출하면 안된다}라는 임무가 추가된다
(1) 인증 & 세션 키
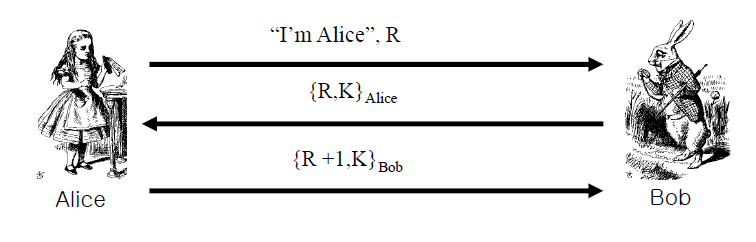
Bob은 Alice가 보낸 Nonce를 암호화할 때 "K"라는 세션키도 같이 암호화한다
이 K는 "Alice야 우리 앞으로 세션키 K로 쓰자"라고 서로 공유하기 위해서 같이 암호화해서 보낸다
그 다음 Alice는 R+1 & K를 암호화해서 Bob에게 보냄에 따라 세션키 공유가 완료되었다
Bob의 입장에서 Alice가 맞는지 확인하는 방법은 "아까 보낸 K" & "받은 메시지 복호화 한 후 얻은 K"가 동일한지 체크하면 된다
하지만 Alice입장에서는 상대가 Bob인지 Trudy인지 확인할 수 없다
>> 세션키 공유 O / 상호인증 X
(2) 공개키 인증 & 세션 키
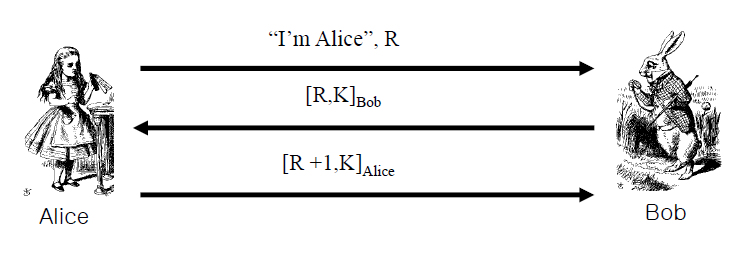
Bob은 Alice로부터 받은 R과 자신이 만든 K를 Private key로 서명해서 Alice에게 전달해준다
>> 내가 Bob이라는 것을 인증하기 위해서 서명을 생성
Alice는 Bob의 Public Key를 통해서 서명을 해제하고, Bob이 보낸 K를 R+1과 함께 자신의 서명을 생성해서 Bob에게 보낸다
>> 내가 Alice라는 것을 인증하기 위해 서명을 생성
따라서 이 프로토콜은 "상호인증"은 된다. 더불어서 세션키도 안전하게 공유가 될까??
서명이 된 것은 Bob이든 Alice든 Public Key로 풀어버리면 되기 때문에 Trudy가 세션키를 볼 수 있다
따라서 세션키가 Attacker에게 노출이 되는 것을 알 수 있다
(3) 선 서명 후 암호화

일단 먼저 전자서명을 하고, 서명을 암호화해서 보내는 것을 확인할 수 있다
"서명"을 통해서 상호인증을 할 수 있고, 암호화를 통해서 세션키를 잘 암호화한걸로 보이는데 이러한 인증 프로토콜은 과연 안전할까??
>> 하지만 MITM Attack이 가능하다
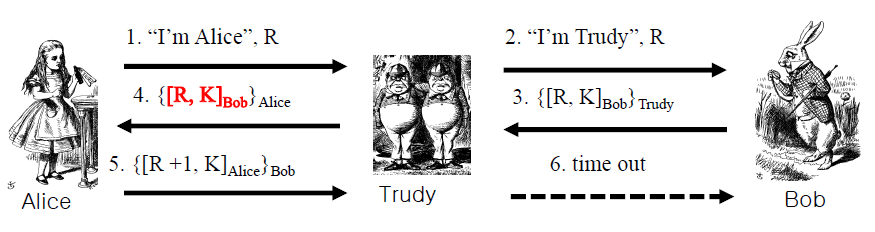
이 목적은 결국 Trudy가 Bob인척하고 Alice와 대화하기 위한 공격이다
따라서 Alice는 Bob에게 먼저 "나 Alice" & R값을 보낸다
하지만 중간에 Trudy가 이 메시지를 가로채서 R값을 Bob에게 본인 이름으로 보내게 된다
Bob은 Trudy에게 자신의 서명을 Trudy's Public key로 암호화한 것을 보내게 된다
>> 여기서 Trudy는 Bob의 서명을 획득하게 된다
Bob의 서명을 획득하자마자 Trudy는 Bob과의 Connection을 끊어버리고 다시 Alice와 대화를 재개한다
Trudy는 Alice에게 Bob의 전자서명을 보내게 되고 이거를 받은 Alice는 Bob이 보냈다고 믿고 인증을 완료한다
따라서 Alice는 실제로는 Trudy와 대화하고 있지만 Bob과 대화하고 있다고 착각한다
(4) 선 암호화 후 서명

위와 같은 공격을 여기서도 한다고 하자
Trudy는 R을 가로채서 Bob에게 보낸다
그러면 Bob은 Trudy와 대화하기 때문에 [{R, K}Trudy]Bob을 보내게 된다
하지만 Trudy가 Alice에게 보내야 하는 것은 [{R, K}Alice]Bob이다
그렇다고 해서 저 전자서명을 풀어버리면 전자서명이 깨지는 것이기 때문에 Trudy는 [{R, K}Trudy]Bob을 Alice에게 그대로 보내게 된다
이걸 받은 Alice는 공격을 감지하고 더이상 대화를 하지 않을 것이다
TimeStamps
이전에는 Replay Attack을 막기 위해서 Nonce를 활용했다
Nonce는 {1. Nonce를 통한 질문 / 2. Nonce를 해결한 응답} 이러한 2단계가 필요하다
하지만 Timestamp를 사용하면 1단계만으로 인증이 완료된다
그냥 해당 시간을 보내고 읽기만하면 되기 때문이다
그러나 Timestamp를 사용하려면 상호간에 시간 sync가 맞아야 한다
여기서 시간을 정밀하게 동기화하는 것은 굉장히 어렵다.
왜냐하면 message를 보낼때는 delay가 발생하기 때문이다
여기서 이러한 delay를 고려하는 것이 "Clock skew"이다
Clock skew는 시간 오차를 얼마까지 허용할까에 대한 값이다
물론 Clock skew가 너무 크면 Replay Attack이 가능할 것이다

이 선 암호화 후 서명 인증 프로토콜은 안전할까???
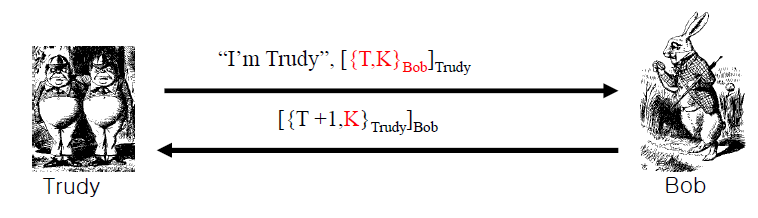
Clock Skew가 1분이라고 설정되어있다면 Trudy는 1분안에 Replay Attack을 수행할 수 있다
따라서 위의 대화간에 Trudy는 Alice가 처음 보낸것을 도청하고, 저 전자서명을 Alice's Public Key로 풀어버리면 {T, K}Bob을 알 수 있다
그리고 이것을 본인의 서명으로 만들어서 Bob에게 전달하면 Bob은 이에 대한 응답으로 본인 서명을 만들어서 Trudy에게 응답할 것이다
여기서 Trudy는 Bob의 전자서명을 깨고 내부에 있는 {T+1, K}Trudy도 본인의 private key로 복호화해버리면 K가 노출된다
따라서 Timestamp + "선 암호화 후 서명"을 사용하면 세션키가 Attacker에게 노출되는 위험이 존재한다
| 선 서명 후 암호화 | 선 암호화 후 서명 | |
| Nonce | 안전 X | 안전 O |
| Timestamp | 안전 O | 안전 X |

위의 문제를 해결할 수 있는 인증 프로토콜이다. 애초에 Alice가 K를 보낸 순간 Bob은 이 K를 받았기 때문에 굳이 한번더 K를 Alice에게 보낼 필요가 없다
따라서 T+1만 보내면 Trudy가 Replay Attack을 해도 세션키 K를 얻을 수는 없다
완전 순방향 비밀성 (PFS : Perfect Forward Securecy)
PFS가 나오게 된 배경은 다음과 같다
<Alice & Bob은 대칭키 K(ab)를 공유하는 상황>
Alice & Bob은 K(ab)로 암호화한 cipher text를 서로 교환하고 있다고 하자
여기서 Trudy는 이 cipher text를 도청한다
도청했는데 K(ab)를 모르니까 복호화 할 수가 없다
근데 나중에 어떤 사건에 의해서 Trudy가 Alice의 노트북을 보유할 수 있게 되었다고 하자
이러면 Trudy는 노트북 안에 존재하는 K(ab)를 사용해서 도청했던 cipher text를 복호화할 수 있을 것이다
이러한 부분이 우려가 되기 때문에 "중요한 Key가 나중에 노출이 되어도 이전에 교환했던 메시지가 노출되지 않게 하는 방법"은 뭐가 있을까라고 생각하다가 나온 방법이 PFS이다
일단 Alice & Bob은 K(ab)를 공유하기는 하지만 이 K(ab)로 메시지를 암호화하면 안된다.
먼저 둘간의 Session을 생성하고 그에따른 세션키가 생성되면 이 세션키(Ks)로 메시지를 암호화해서 서로 교환하자
>> 세션이 종료되면 세션키도 당연히 버릴 것이다
근데 이 방법을 쓰려면 어쨌든 세션키를 만들어야 하고 세션키 만들 때 K(ab)를 쓸텐데 이 부분은 문제가 되지 않을까?

Alice는 Ks를 사용하기 위해서 이 Ks를 K(ab)로 암호화해서 Bob에게 전달하였다
Bob은 Ks를 받고 이제 메시지를 Ks로 암호화해서 서로 교환하기 시작했다
- 세션키 Ks 공유 완료
Trudy는 위의 교환되는 E(Ks, Kab) & E(messages, Ks)를 도청하였다
그리고 나중에 Alice의 노트북을 얻어서 K(ab)를 알아냈다고 하자
이 시점에서 Alice & Bob은 Ks를 버리기는 했지만 Trudy는 K(ab)를 알아냄에 따라 K(s)도 알아낼 수 있다
따라서 최종적으로 Trudy는 E(messages, Ks)를 Ks로 복호화함에 따라 messages를 알아내게 되었다
>> "디피-헬먼 키교환"을 적용해보자

Alice는 a를 생성하고 g^(a) mod p를 K(ab)로 암호화해서 Bob에게 전달한다
Bob은 b를 생성하고 g^(b) mod p를 K(ab)로 암호화해서 Alice에게 전달한다
Alice & Bob은 교환한 값에 따라서 g^(ab) mod p를 계산할 수 있고 이를 세션키로 활용한다
키교환이 완료되었기 때문에 a, b는 노트북에서 지워버린다
나중에 Trudy가 어떻게 해서 K(ab)를 알아냈다고 하자
그런데 g^(a) mod p, g^(b) mod p를 안다고 해서 g^(ab) mod p를 알아내는 것은 굉장히 어려운 일이다 (이산로그 문제)
따라서 Trudy는 a or b를 알아야 하는데 a, b는 이미 노트북에서 지워졌기 때문에 Trudy는 세션키를 알아내지 못한다
이렇게 임시로 키교환을 위해서 디피-헬먼을 사용하는 것을 "일회성 디피-헬먼 : Ephemeral Diffie-Hellman"이라고 한다

{상호 인증 + 세션 키 + PFS}를 모두 만족하는 인증 프로토콜이다
지식-제로 증명 (ZKP : Zero Knowledge Proof)
Alice는 "비밀 P"를 알고 있다
이 때 Alice는 "나는 P를 알고 있어"라고 Bob에게 자랑하고 싶어한다
여기서 Alice는 자랑은 하는 대신 Bob에게 "비밀 P"를 직접 알려주고 싶지는 않다
이 때 사용하는 증명이 지식-제로 증명이다
Bob은 "비밀 P"에 대한 어떤 정보도 입수하지 않았더라도 Alice가 "비밀 P"를 알고있음을 확인할 수 있어야 한다
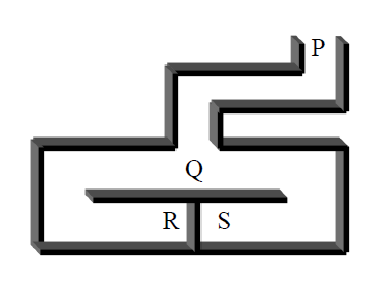
이러한 통로에서 Alice는 "R이든 S든 <열려라 참깨>를 외치면 문이 없어지는 비밀"을 알고 있다고 하자
이 비밀을 Bob에게 직접적으로 알려주기는 싫고 "나는 문에 대한 비밀을 알고있어"라고 자랑하고 싶어한다
여기서 Bob은 R & S중 하나를 골라서 "Alice야 이쪽으로 와봐"라고 말했다
만약 Alice가 R에 있고 Bob이 R쪽으로 간다고 하면 Alice는 비밀을 알든 모르든 R에서 나타날 수 있다
그리고 Alice가 문을 열어서 S로 가고 Bob도 S쪽으로 간다고 하면 Alice는 비밀을 알기 때문에 R -> S로 갈 수 있었다
따라서 여기서 Alice는 비밀 주문을 모르고 있다면 1/2확률로 Bob을 속일 수 있다
하지만 이 프로토콜이 n번 반복된다면 Alice가 Bob을 속일 수 있는 확률은 (1/2)^(n)이 될 것이다
따라서 Bob은 아주 높은 확률로 Alice가 비밀을 진짜 알고 있다고 믿을 수 있다

Fiat-Shamir Protocol
여기서는 modulo N상에서의 제곱근을 활용한다
이 문제는 굉장히 풀기 어렵다
N = pq : p, q는 소수
Alice는 "비밀 S"를 안다고 하자
v = S^(2) mod N
public : N & v
secret : S
Alice는 여기서 Bob에게 "나는 S알고있어"라고 증명해야 한다
그리고 S와 관련된 어떠한 정보도 노출되지 않는다고 가정하자
N & v는 public이므로 모든 사람들에게 노출이 된다

이 프로토콜을 수행해준다
Alice는 Random한 값인 r을 선택해서 x = r^(2) mod N을 구해서 Bob에게 전달한다
Bob은 {0, 1}중 하나를 random하게 골라서 Alice에게 전달한다
Alice는 r*S(e) mod N을 구해서 Bob에게 전달한다
여기서 식을 잘 변형시키면 y^(2) = x*v^(e) mod N이 나오게 된다
따라서 Bob은 이 식을 검증하게 된다
