2022. 5. 14. 16:47ㆍMajor`/인공지능
Supervised Learning에서 Agent는 인간이 부여한 몇가지의 Example을 통해서 학습을 한다고 설명했다
이 때 Agent는 Example들에 대한 "가설 함수"를 찾아내는 것이 학습의 목적이다
당연히 Agent가 가설함수를 도출해냈으면 그 가설함수에 대한 "평가 & 선택"을 해야 한다
모델 선택
최종 결정되는 모델은 결국 여러 가설함수중 Best를 선택할 것이다
1. Model Selection
"가설 공간"을 정의한다
가설 공간은 그냥 다항식의 차수를 의미한다
2. Parameter Optimization
가설 공간내에서 최고의 가설 함수를 찾아야 한다
결국 다항식의 차수를 인간이 결정해주었다면 Agent는 그 다항식에 대한 "계수"를 Learning을 통해서 알아내야 한다
※ 모델 복잡도
모델이 복잡해진다는 의미는 다항식의 차수가 올라간다는 것이고 결론적으로 "계수"가 많아진다는 뜻이다
계수가 많아지면 Agent가 알아내야할 것들이 많아지기 때문에 훈련 데이터의 양 & 학습 시간도 비례해서 증가하게 된다
※ Error Rates (Validation Set vs Training Set)

결국 가설함수는 부여받은 학습 데이터를 거의 99.999% 만족시켜야 한다.
그러려면 결국 모델의 복잡도를 증가시켜 가면서 가설함수를 구해야 한다.
하지만 여기서 학습 데이터에 너무 과도하게 맞추려고 해서 모델의 복잡도를 계속 증가시키면 "학습 데이터에 대한 Overfitting"이 되어서 결국 나중에 검증을 위한 Test-Set에 대한 Error Rate가 증가하게 된다
따라서 "일반화"에서는 오히려 모델의 복잡도가 과도하게 높을경우 손해를 볼 가능성이 있다
손실 함수
일반적으로 위에서 설명한 Error Rate는 손실 함수에 포함되는 개념이다
결국 손실 함수는 가설함수로부터 얻은 "예측 값"이 목적함수로부터 얻은 "실제값"에 비해서 얼마나 손실이 발생했는지를 알아낼 수 있는 함수이다
L(x, y, y`)
실제값(목적함수) : f(x) = y
예측값(가설함수) : h(x) = y`
결국 y와 y`의 차이를 알아내야 한다
1) 0/1 Loss : "L(0/1) Loss Function"
L(x, y, y`)에서 y와 y`이 다르면 1 & 같으면 0을 return하는 손실함수이다
<10개의 훈련 데이터>
여기서 4개의 case는 y와 y`이 다르다고 하면
>> 손실함수는 4를 return하게 된다 (4개가 다르기 때문에)
따라서 손실율 : Error Rate는 "4/10 = 0.4"가 된다
2) Absolute Value Loss : "L1 Loss Function"
L1(y, y`) = |y-y`|
결국 Error Rate와 동일한 값을 도출하게 된다
- 정답 & 예측치의 오차를 "실제로" 계산
<10개의 훈련 데이터>
목적함수 output : <1 2 3 4 5 6 7 8 9 10>
가설함수 output : <2 1 3 4 6 5 7 8 7 8>
여기서 손실함수를 적용하면 {1 + 1 + 0 + 0 + 1 + 1 + 0 + 0 + 2 + 2} = 8이 된다
따라서 손실율 : Error Rate는 "8/10 = 0.8"이 된다
3) Squared Error Loss : "L2 Loss Function"
L2(y,y`) = (y-y`)2
{정답 - 예측치}를 더 키우기? 확실하게 하기위해서 제곱값을 사용하는 경우도 있다
결국 L1을 쓰든 L2를 쓰든 "테스트용 데이터"는 굉장히 많기 때문에 각 테스트용 데이터마다 L의 값은 다르다
>> 전체 테스트용 데이터에 대한 모든 손실 집합을 실제 손실로 본다


최고의 가설 선택
실험적 손실
실험적 손실은 훈련 데이터 E에 대한 각 데이터 손실값에 대한 평균을 나타낸다
>> 따라서 실험적 손실을 최소화하는 가설함수가 최고의 가설함수일 것이다
- 그냥 손실함수에 의해서 도출되는 손실율이 가장 작은 가설함수가 Best라는 말이다

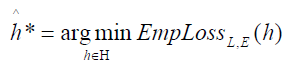
가설 평가
"Error Rate of a Hypothesis"
결국 여러 가설함수중에서 손실함수에 의한 손실율이 가장 작은 가설함수를 Best로 생각해서 선택하였다
그러면 이제 선택한 가설함수를 "평가"해야 한다
평가할때는 "학습 데이터"와는 다른 "테스트 데이터(검증 집합)"를 활용해서 평가한다
당연히 가설함수는 "학습 데이터"에 의존해서 만들어졌기 때문에 학습 데이터에 대해서는 오류율이 굉장히 낮을지는 몰라도 실제 테스트 데이터에 대해서는 오류율이 어떻게 나올지 가늠하기 힘들다
만약 테스트 데이터(검증 집합)에 대해서도 오류율이 낮다면 해당 가설함수는 목적함수 F에 꽤 가까운 가설함수라고 할 수 있을 것이다
▶ 훈련 집합
이 훈련 집합을 통해서 Agent가 Learning을 해서 가설 함수를 찾아낸다
- 훈련 데이터에 대해서 Agent는 적어도 90% 이상의 정확도를 가져야 한다
▶ 검증 집합
Agent가 도출해낸 가설함수를 평가하기 위한 집합
- 마찬가지로 labeled data이다
▶ 테스트 집합
검증을 통해서 최종적으로 결정한 가설함수에 대한 테스트를 하기 위한 집합
사실 테스트 집합이나 검증 집합이나 거의 똑같은 개념이다
하지만 AI 경진대회의 경우 참가자들에게는 {훈련 집합 / 검증 집합}을 부여한다. 이후 참가자들이 제출한 결과물에 대해서 테스트 집합으로 검사해서 등수를 매긴다
교차 검증 (Cross-Validation)
일반적으로 존재하는 모든 경우의 학습 데이터를 전부 부여해서 학습시키는 것은 아니다
Cross-Validation은 {학습 데이터 / 검증 데이터}를 역할을 서로 바꿔가면서 성능을 평가해보겠다는 검증 방법이다
1. Holdcut Cross Validation
부여받은 데이터(학습 데이터)를 Random하게 Split해서 {학습 데이터 / 테스트 데이터}로 나누는 방식이다
Labeled Data를 "처음부터" {학습 / 검증} 둘로 나누어서 활용한다
- 일반적으로 학습 데이터의 비율을 더 많이 부여한다
분리된 학습 데이터를 가지고 학습을 진행하고, 학습이 다 진행된거 같으면 "검증 데이터"들을 통해서 검증을 한다.
이렇게 1단계를 통해서 나온 성능을 그냥 최종 성능으로 결정한다는 것이다
HoldCut의 경우 테스트 셋이 모델의 파라미터 설정에 큰 영향을 미치게 된다
그리고 모델이 테스트셋에 Overfitting될 가능성이 존재한다
2. K-Fold Cross Validation

전체 데이터를 "K개의 그룹"으로 Split한다
- 일반적으로 K는 홀수
1. 전체 K개의 그룹 중에서 "하나의 그룹"을 뺀 나머지 "K-1개의 그룹"을 학습에 사용한다
2. 뺀 "하나의 그룹"을 "K-1개의 그룹을 통한 학습"의 검증 데이터로 활용한다
>> 이 과정을 K번 반복한다
- 물론 각 단계에서 선택되는 검증 집합은 "이전에 검증 집합으로 사용되지 않은 집합"중에서 선택된다
K-Fold Cross Validation의 경우에는 총 데이터 개수가 적은 데이터 셋에 대한 정확도를 향상시킬 수 있다
단점은 일반적인 {훈련 셋, 테스트 셋}을 통해서 진행하는 학습법에 비해 시간 소요가 크다
3. Leave-One-Out Cross Validation
LOOCV는 K-Fold Validation의 굉장히 극단적인 검증 방법이다
K-Fold는 "하나의 그룹"을 검증 데이터로 쓰지만, LOOCV는 그룹이 아니라 "단 하나의 데이터"를 검증 데이터로 사용하는 것이다
"데이터가 많으면 되도록이면 K-Fold를 활용하고 데이터가 너무 적다면 LOOCV를 활용한다"
선형 모델 (Linear Models)
선형 모델이란 "일차식 가설함수"를 찾겠다는 의미이다

여기서는 {소득액 / 평균 1회 구매액 / 구매횟수}라는 "계수"를 통해서 "예상구매액"을 얻고 싶다
"예상구매액"은 어떤 변수에 의한 값으로 도출되기 때문에 Regression이라고 볼 수 있다
따라서 input이 3개가 들어가기 때문에 Agent는 Learning을 통해서 총 4개의 파라미터를 알아내야 한다

여기서는 {소득액 / 평균 1회 구매액 / 구매횟수}라는 "계수"를 통해서 "고객등급"을 얻고 싶다
"고객등급"은 어떤 변수에 의해서 도출된 output을 카테고리화 시키는 것이기 때문에 Classification이라고 볼 수 있다
input 3개가 존재하기때문에 Agent는 Learning을 통해서 총 4개의 파라미터를 구한다
그리고 구해진 가설함수에 input을 넣어서 도출된 output을 "Classification Threshold"에 적용해서 분류시킨다
선형 회귀/분류 둘다 Linear Model을 사용하지만 input을 적용시킨 output을 활용하는 방식에 차이가 존재한다
>> 회귀 : output 그대로 활용
>> 분류 : output을 어떤 기준에 의해서 나뉘어진 것을 활용
회귀는 continuouos하다고 볼 수 있지만, 분류는 Discrete하다고 볼 수 있다
선형 회귀 (Linear Regression)

가로축은 "면적"을 나타내고 세로축은 "가격"을 나타낸다
따라서 여기서는 "면적에 따른 가격"을 Regression을 통해서 구하고 싶다
선형 회귀는 input이 "1차원"으로 들어온다고 볼 수 있다
- 1차원 input에 대해서 output이 continuous하게 나오기 때문
Agent는 여러 사례를 통해서 Learning을 하고 Learning에 의해서 얻은 함수는 다음과 같다

※ 일변수 선형 회귀

Learning을 통해서 "손실율"이 가장 작은 가설함수 H = 0.232x + 246을 찾아내었다
- w1 = 0.232
- w0 = 246
>> 여기서 "Best 가설함수"는 어떻게 찾을 수 있을까? 손실율이 가장 작다는 의미는 그래프상에서 어떤 의미일까?
오른쪽 Loss Function 그래프는 {w1, w0}가 변함에 따라 가설함수의 손실율이 얼마인지를 나타내는 그래프이다
Squared가 된 것을 보니까 Loss Function으로 L2를 사용했다는 것을 알 수 있다
>> Loss가 가장 작을 때 {w1, w0}는 어떻게 찾을까?? "미분"을 활용하자
기울기 하강에 의한 점진적 계수 변경

가설함수의 Loss Function은 위와 같다
여기서 최종 식을 w0에 대해서도 미분해보고, w1에 대해서도 미분해보자

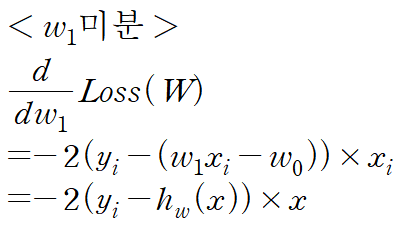
따라서 미분에 의해서 {w0 & w1}은 다음과 같이 변경된다

여기서 α는 나중에 인간이 정해주는 "학습율(Learning Rate)"이다
- 학습율이 높을 수록 변화폭을 많이 반영시켜준다
▶ 일괄적 기울기 하강 (Batch Gradient Descent)

N개의 학습 데이터 전체에 대한 오차를 다 더해서 그 값을 가지고 가중치를 updtae하는 방식이다
- N개의 오차가 다 모일때까지 가중치에 대한 update가 발생하지 않는다
>> 그러면 N개의 학습 데이터 전체에 대한 오차 값을 가중치에 update할 때 적용하면 학습이 끝난건가??
아니다. update하고 나서 Loss가 최소가 될때까지 이 과정을 계속 반복한다
여기서 매번 똑같은 N개의 학습 데이터를 적용시키지 않느냐에 대한 의문이 생길 수 있지만 "가설함수 h"를 자세히 보면 {w0, w1}을 포함하고 있다
따라서 N개의 훈련 데이터를 반복적으로 사용해서 {w0, w1}이 계속 변하기 때문에 결국 가설함수가 변하게 된다.
그러므로 매번 똑같은 예측값이 나오는게 아니라 다른 예측값이 나오게 된다
- N개의 훈련 데이터 전체를 고려해서 udpate하기 때문에 "Global Maximum에 대한 수렴성"이 보장된다
- 하지만 N개의 훈련 데이터에 대한 오차를 전부 계산해야 하기 때문에 속도가 느리다
▶ 확률적 기울기 하강 (Stochastic Gradient Descent)

학습데이터 "1개"에 대해서 오차를 구하고 그 값을 가지고 가중치를 update하는 방식이다
- 1개의 학습 데이터만 고려해서 update하기 때문에 Batch보다 속도가 빠르다
- 하지만 1개의 훈련 데이터에 대한 오차만 고려하기 때문에 "Local Maximum"에 빠질 위험이 존재한다
▶ MiniBatch Gradient Descent
MiniBatch란 {Batch + Stochastic}이라고 보면 된다
N개의 학습 데이터 전부를 고려하는게 아니라 임의로 정한 K개를 고려해서 가중치를 update하는 방식이다
- 1000개의 학습 데이터가 있다면 100개씩 쪼개서 100개의 오차가 모일때마다 update해주기
선형 분류 (Linear Classification)

현재 Class Label은 {Explosion(핵폭발) / Earthquake(지진)}이다
그리고 input으로 들어오는 2차원 값은 {x1, x2}이다 :: x1, x2는 S파/P파이다
따라서 input으로 들어오는 2차원 값의 "value"를 통해서 어느 Class Label로 들어갈지 결정이 된다
Classification은 결국 "결정 경계"를 통해서 2차원 입력 (x1, x2)를 분류해준다

이러한 경우는 "Linear Decision Boundary"로 정확하게 분류하지 못할 것이다
따라서 이때는 "비선형 결정 경계"를 통해서 Classification한다
1) 결정 경계 : Hard Threshold

이러한 학습 데이터를 Classification하기 위한 결정 경계를 다음과 같이 구했다고 하자

여기서 Hard Threshold란 "엄격한 기준 값"이 존재해서 그 값을 통해서 Classification한다는 의미이다

결정 경계에 {x1, x2}를 넣었을 경우 그 값이 0이상이면 1로 분류되고, 0미만이면 0으로 분류된다
▶ Hard Threshold 가중치 Update Rule : "퍼셉트론 학습 규칙"

아까 Regression에서 봤던 기울기 하강 공식 그대로 적용하는 것을 볼 수 있다
α란 "학습률"을 의미하고 이 "학습률"에 의해서 weight의 변화폭을 결정한다

x축은 "가중치 update 횟수"이다. 따라서 그래프는 학습이 진행됨에 따라 정확도를 나타낸 것이다
학습률을 고정시킨 2개의 그래프를 보면 "진동"이 심하게 보이는 것을 볼 수 있다
그에 반해서 학습률을 시간(update 횟수 증가)에 따라 조정한 마지막 그래프를 보면 "진동"이 많이 감소한 것을 볼 수 있다
- 처음에는 학습률을 1로 지정해서 그대로 반영되지만 시간(update 횟수 증가)이 지남에 따라 덜 반영한다고 추론할 수 있다
>> "진동"이 생기는 이유는 엄격한 기준인 Hard Threshold를 사용했기 때문이다
2) 결정 경계 : Logistic(Sigmoid) Function
Hard Threshold를 사용해도 결국 "미분"을 통해서 가중치를 update한다

하지만 함수는 0에서 불연속인 함수이기 때문에 이 자체를 미분하기는 좀 어렵다
그리고 실제로 output은 차이가 별로 나지 않을 수 있지만 Hard Threshold를 적용하면 {0 / 1}중에 하나로 급격하게 변화하기 때문에 "학습 불안전성"이 존재한다
>> 따라서 Hard Threshold 대신에 "Logistic/Sigmoid Function"을 활용하자
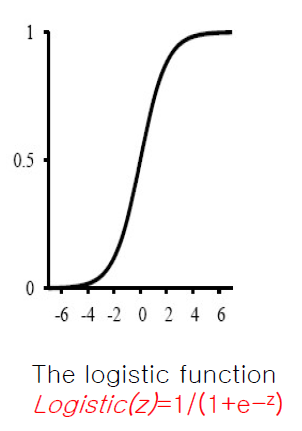
Logistic/Sigmoid Function은 Hard Threshold와는 다르게 "연속 함수"이므로 미분하기가 편리하다
그리고 output과 상관없이 {0 / 1}로 분류되는게 아니라 output이 "e"에 영향을 준다
이 Logistic Function의 범위는 [0, 1)이 될 것이다
- 지수항이 존재하고 지수항은 어차피 0은 안되기 때문에 Logistic Function의 최댓값은 아무리 커도 1보다는 작다
▶ Logistic/Sigmoid Function 가중치 Update Rule : "체인 학습 규칙"

Logistic에서의 가중치 update rule도 "미분"을 활용하기는 하지만 아까 "퍼셉트론 학습 규칙"과 다른점은 빨간 밑줄 부분이 포함되었다는 점이다
미분을 통해서 위의 빨간 밑줄 부분이 도출된 과정은 다음과 같다


위의 Hard Threshold와 동일한 데이터에 대한 학습 과정인데 Hard Threshold와 달리 Logistic Function을 적용했더니 더 빨리 수렴하고 학습의 불안전성이 거의 없는 것을 볼 수 있다
