2022. 4. 16. 22:21ㆍMajor`/인공지능
Adversarial Search (적대적 탐색)
이전의 여러가지 탐색(BFS, DFS, A*, GBFS, Hill-Climbing, Local Beam, Simulated-Annealing)들은 전부 "Single Agent 환경"에서의 탐색 문제이다
Multi Agent의 경우에도 현재 노드에서부터 Tree 형태로 Expanding되는 것은 동일하다고 볼 수 있다
- Adversarial Search에서는 "Game Tree"라고 부르기도 한다
Single Agent에서의 탐색 목적
Single Agent는 풀고자하는 문제/환경에 Agent혼자만 존재하고 환경 또한 Agent 혼자만 변경이 가능하다
>> Single Agent에서의 탐색은 결국 초기 상태 -> 목표 상태까지의 Sequence Of Action을 결정하는 것이고, 실제로 Sequence Of Action을 차례대로 수행함으로써 목표 상태에 도달한다
Multi Agent에서의 탐색 목적
Multi Agent는 풀고자하는 문제/환경에 Agent 여러명이 존재하고 환경 또한 Agent 여러명이 변경할 수 있다
Multi Agent에서의 탐색은 당연히 상대방이 어떤 행동을 할지 모른다는 가정에서 그 상태에서 나한테 가장 유리한 행동이 무엇인지 탐색을 통해서 결정한다
>> Multi Agent에서의 탐색은 Sequence Of Action을 결정하는 것이 아니라 "현재 그 상태에서 나한테 가장 유리한 행동 하나"만을 결정한다. 그리고 행동을 결정해야할때마다 탐색은 새롭게 수행된다
Example) 2-Player Game Search Tree

당연히 root node로부터 가능한 경우의수를 Expanding할 것이다
하지만 왼쪽에 보면 MAX? MIN? TERMINAL? UTILITY? 이런것들이 적혀져 있다
물론 게임은 2명이서 하지만 일단 "나(Agent)"를 기준으로 상대방이 어떻게 둘것인가를 예측하면서 Game Tree를 펼쳤다
그래서 MAX의 경우 "내"가 두는 수를 의미하고, MIN의 경우 상대방이 두는 수를 의미한다
당연히 "나"를 기준으로 상대방은 Utility가 가장 낮은 :: 가능한 경우의 수중에 최악의 수를 선택하는 것이 "나"한테는 좋기 때문에 상대방의 turn에는 MIN을 선택한다
Terminal은 더이상 가능한 경우의 수가 없는 경우이고 이 때 1) 승부가 나거나 2) 더 이상 진행이 되지 않는 경우이다
적대적 탐색에서의 완전성/최적성
일반적 Single Agent에서의 탐색의 완전성/최적성의 의미는 다음과 같다
- 완전성 : 주어진 탐색에서 반드시 Solution을 찾을 수 있는가
- 최적성 : 찾은 Solution이 전체적으로 최적의 Solution인가
하지만 적대적 탐색에서의 완전성/최적성의 의미는 약간 다르다
- 완전성 : 여러 State 중 결정을 내릴 수 있느냐
- 최적성 : 여러 State 중 내린 결정이 최적의 결정인가
1) Minimax Search

DFS를 기초로 한 탐색 방식이다
마찬가지로 현재 → 미래(예측)으로 계속 Tree를 확장시키는 방식이다
하지만 값을 매기는 방식이 다르다
Search가 진행되면서 어차피 Search가 종료되는 Terminal단계에는 반드시 도달할 것이다
이에 따라서 Terminal Node는 정확한 Value를 측정할 수 있다
>> Terminal Node에서부터 거슬러 올라오면서 나머지 node들의 value를 측정하는 탐색 방식
Minimax Search의 가정
1) 상대방도 나와 동일한 "상태 평가 함수"를 보유하고 있다
2) 상대방도 나처럼 "최선의 선택"을 항상 하려고 노력할 것이다
- 여기서 "최선의 선택"이란 결국 본인의 차례에는 Highest-Value를 선택할 것이라는 의미이다
>> 이 2가지의 가정을 토대로 탐색이 진행된다
위에서 설명한대로 Game Tree를 확장하는 상상은 상대방과 교류하면서 할 수 없기 때문에 "나만의 상태 평가 함수"를 가지고 확장시켜야 한다
물론 "상태 평가 함수"는 상대방도 동일하게 보유할 수 있다
당연한 말이지만 "내"가 혼자 상상하면서 확장할 때 "내꺼"는 당연히 Highest-Value를 선택할 것이고 "상대방꺼"는 Lowest-Value를 선택할 것이다

현재 Termainal(빨간 테두리)까지 전부 진행이 완료되었고 각 Termainl에서의 Value는 위와 같다
이 때 (1), (2), (3), (4), (5)의 Value는 어떻게 구할까?
MAX라인의 Node : 자식들의 value 중에서 MAX 값
MIN라인의 Node : 자식들의 value 중에서 MIN 값
이에 따라서 (1)의 value는 10이 되고, (2)의 value는 -10이 된다

(3) : 자식들의 value(-10, +10)중에서 MIN값은 -10이므로 "-10"
(4) : 자식들의 value(-10, +10)중에서 MIN값은 -10이므로 "-10"
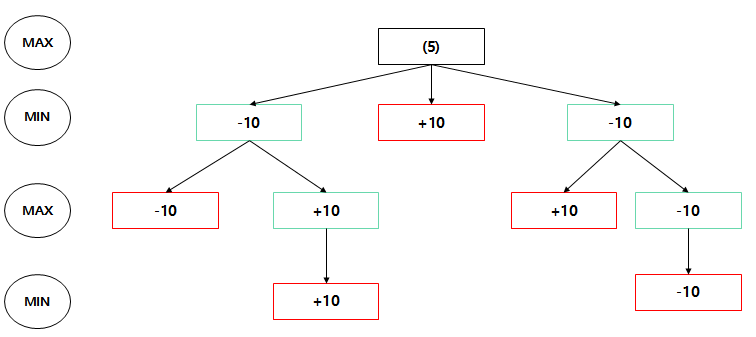
최종적인 root노드의 value는 자식들의 값(-10, +10, -10)중에서 MAX이므로 "+10"이 된다
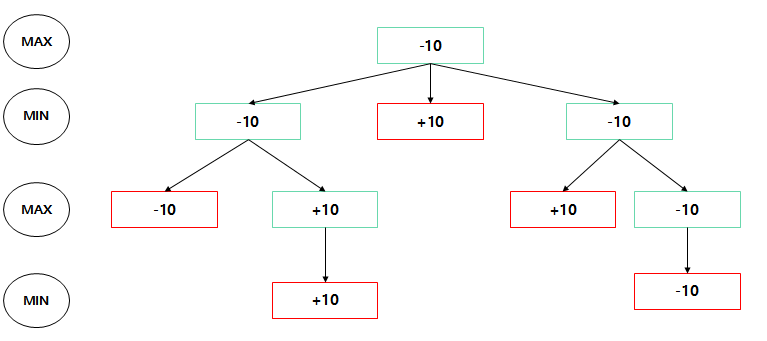
Minimax Search는 "root node에 대한 평가"를 수행하게 되면 탐색은 종료된다
>> Solution : root node에서부터 시작해서 "자신의 값과 동일한 child node로 가기"
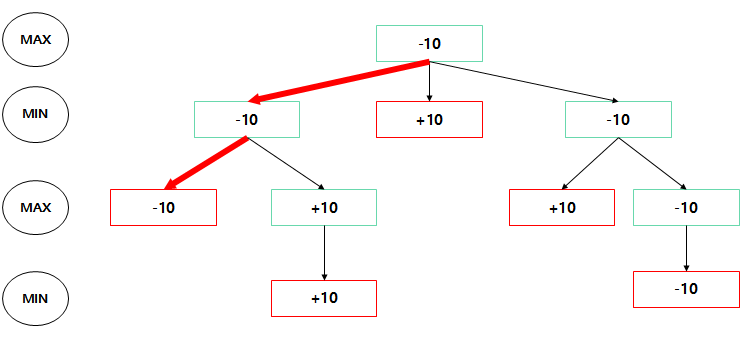
Minimax Algorithm 평가
| Minimax | 만족? 불만족? | 이유 |
| 완전성 | O | Tree가 유한하다면 완전성을 보장해준다 |
| 최적성 | O | 상대방이 최적의 선택을 하든 최악의 선택을 하든 나는 MIN & MAX 계산에 의해서 항상 최적성을 보장한다 |
| 시간 복잡도 | O(bm) | |
| 공간 복잡도 | O(bm) | |
하지만 여기서 Time Complexity가 문제가 된다
Chess의 경우를 생각해보자 (b = 35 / m = 100)
이러면 Time Complexity는 O(35100)이 된다
이 시간복잡도는 사실상 탐색을 할 수 없는 경우가 된다 (모두 탐색)
결국 state로부터 다음 state를 Expanding하는데 이 경우의 수가 너무 많아서 사실상 시간내에 탐색이 불가능하다
Time/Resource Limits :: Minimax Cutoff Search
위의 저런 말도안되는 시간복잡도를 어떻게 해결할까?
→ 깊이 제한(탐색 절단)
→ 상태 평가 함수
- "비 단말 State"에 대한 평가 함수
모든 state를 끝까지 (깊이) 탐색하지 말고 "어느정도의 깊이"를 제한해서 탐색을 해라
- x수 앞까지만 생각
근데 깊이를 제한해서 탐색을 완료했는데 그 완료된 state가 Terminal이 아닐 수 있다
>> 이 때 Terminal이 아닌 node에 대한 "상태 평가 함수"가 반드시 필요하다
다시 이러한 깊이 제한을 chess에 도입하게 된다면
- 106개의 state를 미리 계산
106 ≒ 354
따라서 4수앞까지 생각해볼 수 있다 :: 깊이 제한 = 4
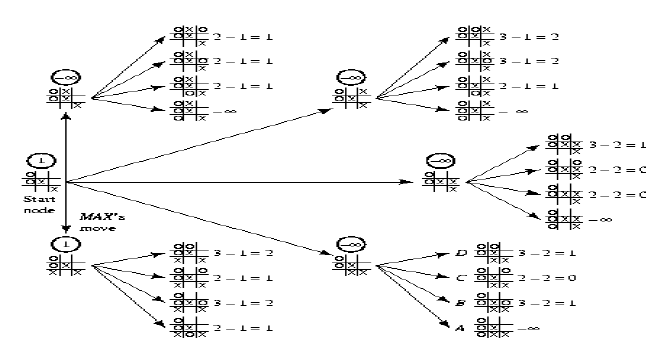
Example) Tic-Tac-Toe Game
Depth Limit : 2
O : 나
X : 상대방
일단 먼저 가정을 하고 가자면

이 그림은 결국 하나의 상태로부터 돌리면 전부 동일하기 때문에 하나의 state를 대표적으로 사용
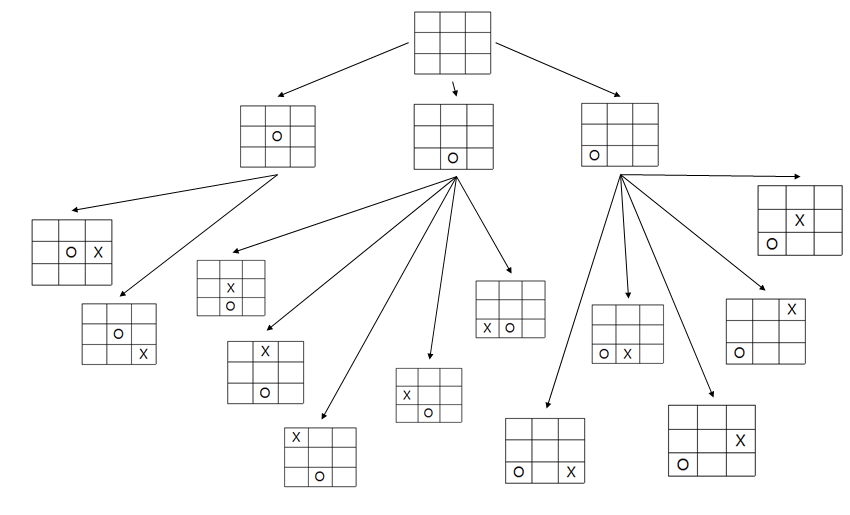
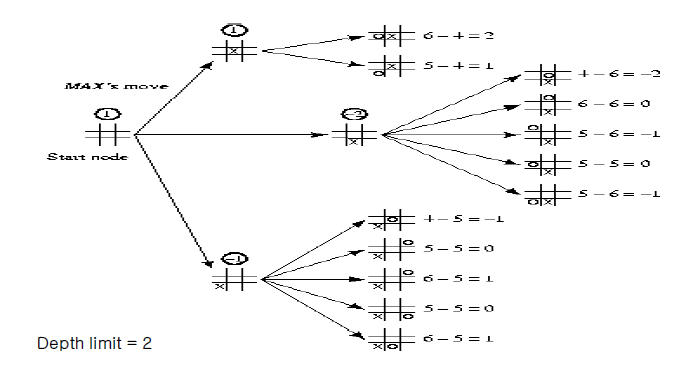
root node로부터 depth limit(2) 까지의 node Expanding을 표현했다
이제 "비단말 노드"에 대한 "상태 평가 함수"를 정의해야 하는데 "상태 평가 함수"는 다음과 같다
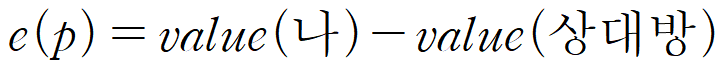
value(나)는 "내가 지금부터 잘 두면 이길 수 있는 경우의 수"이다
value(상대방)도 마찬가지이다
- 여기서 각자 상대방의 수를 생각하지말고 오직 자신만 둔다고 생각하면 된다
이러한 방식으로 위의 Game Tree에 대한 "상태 평가 함수"를 적용하면 다음과 같아진다
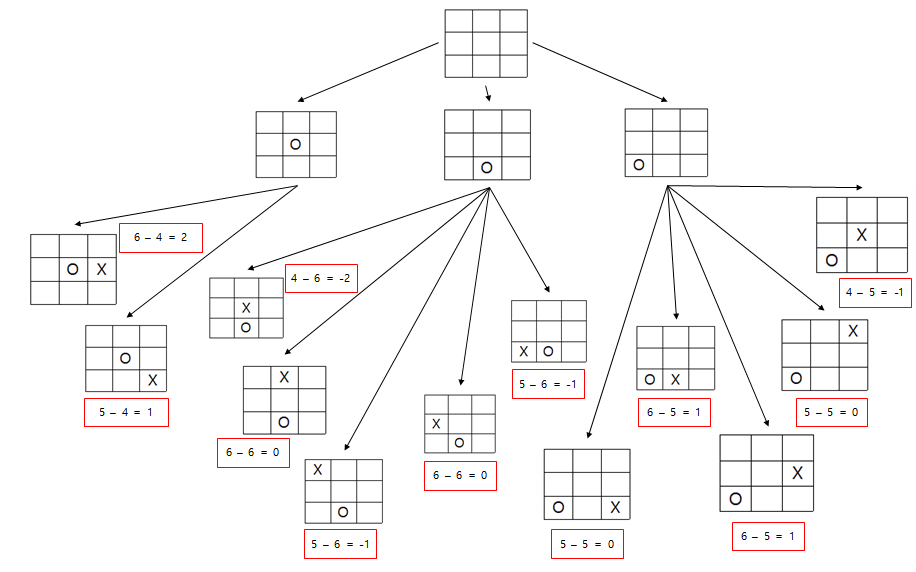
이제 비단말 노드에 대한 "상태 평가"를 했으니 비단말 노드들에 대한 "부모 노드"의 value를 정해줘야 한다
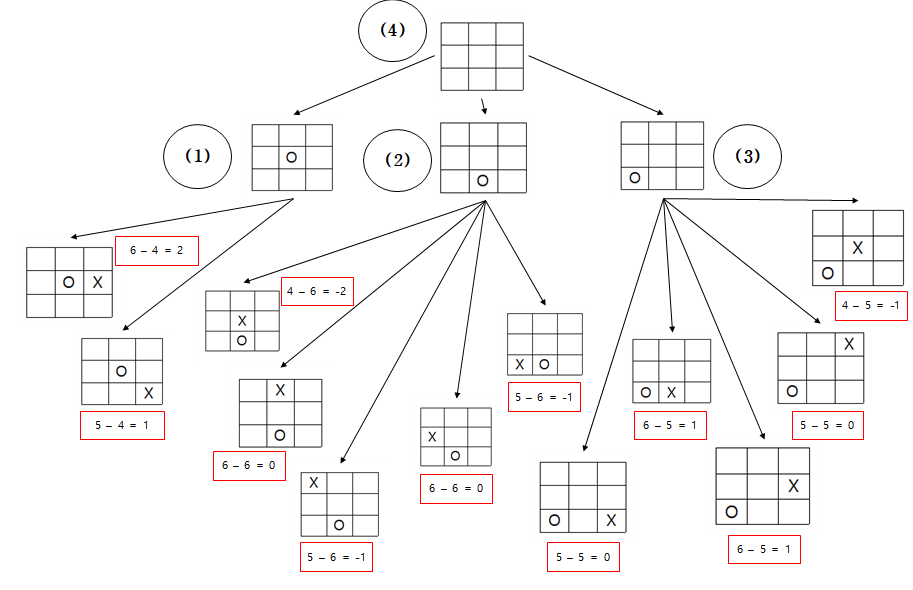
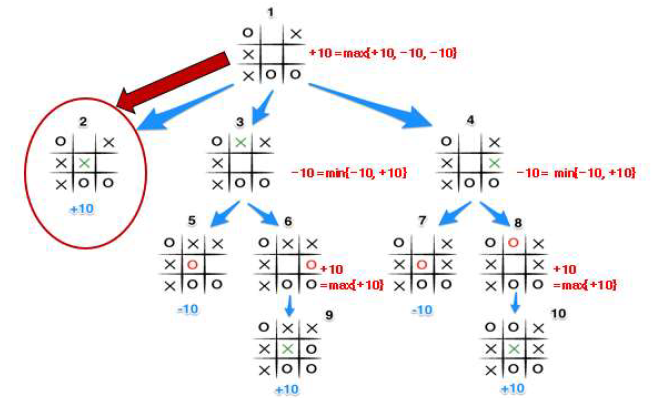
(4)는 root node이니까 MAX Line이다
그러면 (1), (2), (3)은 MIN Line이 될 것이다
(1) : Math.min(2, 1) = 1
(2) : Math.min(-2, 0, -1, 0, -1) = -2
(3) : Math.min(0, 1, 1, 0, -1) = -1
(4) : Math.max((1), (2), (3)) = (1) = 1
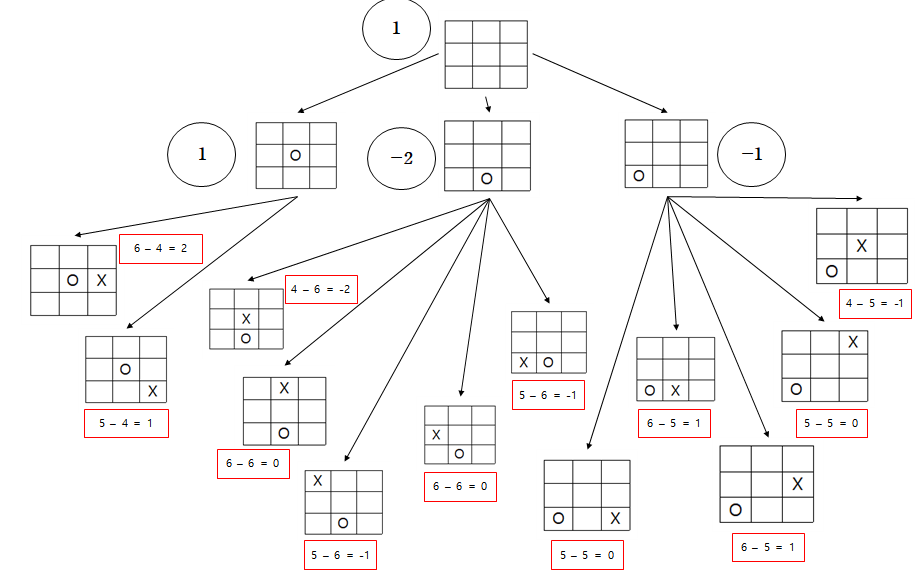
따라서 root node가 평가되었기 때문에 탐색은 종료가 되었다
root node의 value는 1이고 chile node중 value가 1인 node로 진행을 할 것이다
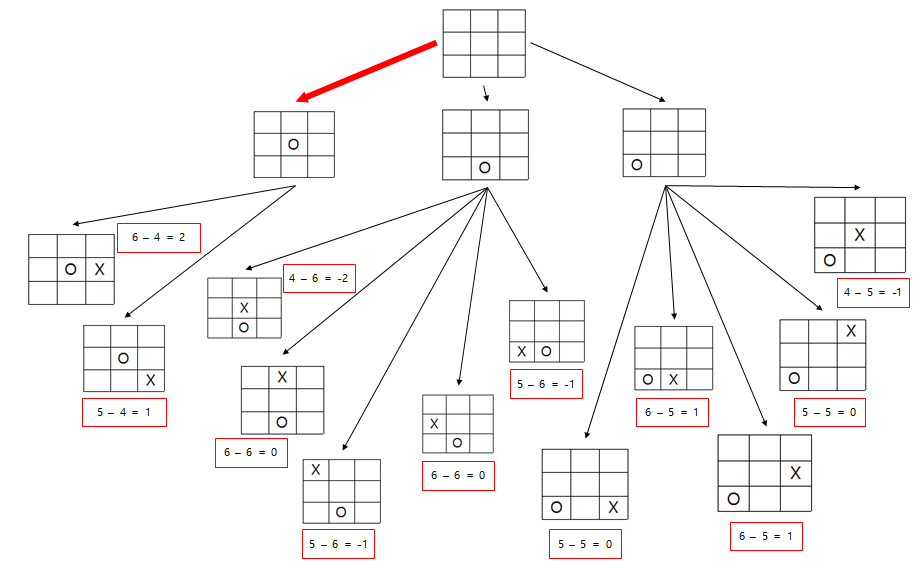
물론 여기서 상대방이 아래 2가지 child중에 어떤것을 선택할지는 모른다
상대방이 어느 곳에 수를 두었다면 그 수로부터 다시 위와 같은 계산을 통해서 Game Tree를 펼치면 된다
- 물론 "내"가 생각한 "상대방의 최적의 수"를 상대방은 그대로 두지 않을 수 있다
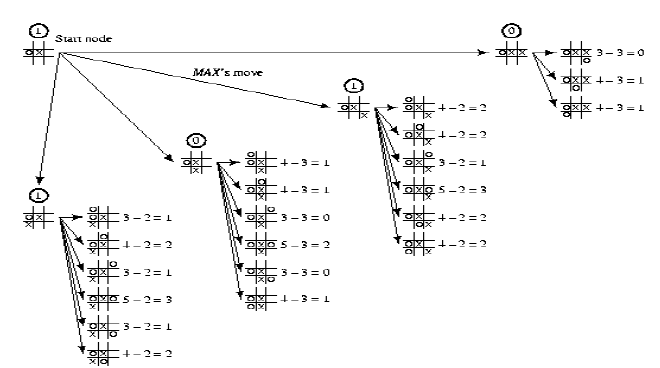
2) α - β Pruning (알파-베타 가지치기)
이 탐색방법은 Minimax를 기초로 한 탐색방법이다
하지만 Minimax와는 달리 "불필요한 계산"을 하지 않는 방식이다
- 불필요한 계산이 소요되는 node는 가지치기를 통해서 없애기
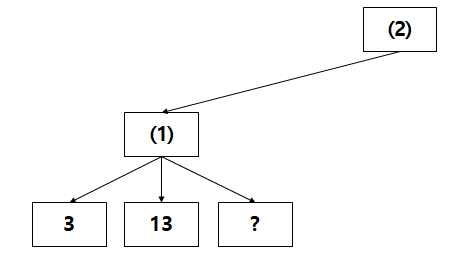
이러한 Game Tree가 현재 탐색되었다고 하자
그러면 (1)은 MIN Line이므로 다음과 같이 계산될 수 있다
value(1) = Math.min(3, 13, "?")
"?"값이 무엇인지 아직 확실하게 모르지만 여기서 얻을 수 있는 정보는 다음과 같다
(1) ≤ 3
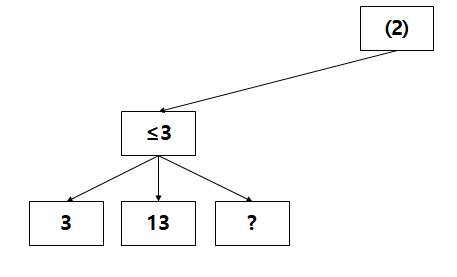
최소한 "3보다는 작거나 같다"라는 사실을 알 수 있다
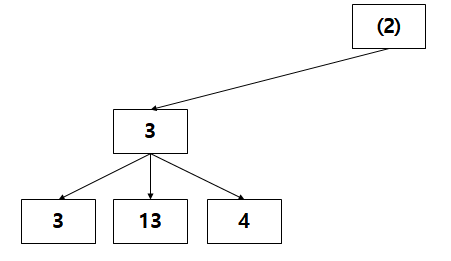
"?"의 값이 4인것을 확인했으니까 (1)의 value는 최종적으로 3이 되었다
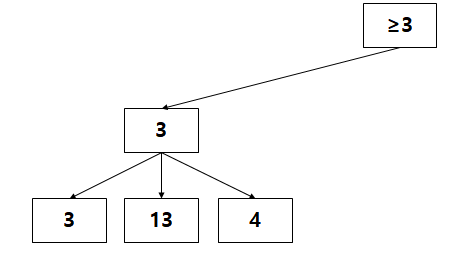
이러면 자연스럽게 root node의 value는 "최소한 3보다 크거나 같다"라는 사실을 파악할 수 있다
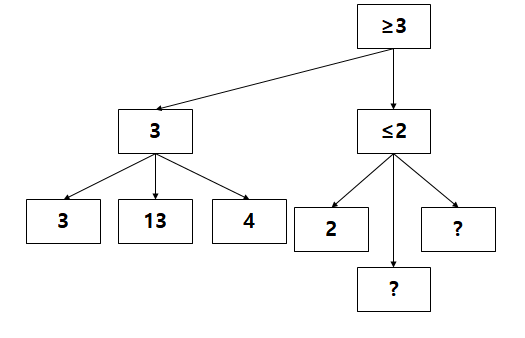
더 탐색을 진행해보니까 Game Tree가 위와 같이 펼쳐졌다
이 때 2번째 child node는 "최소한 2보다는 작거나 같다"의 value를 갖게 된다
하지만 root node는 본인의 chile node 중 MAX 값을 본인의 value로 설정하게 된다
이미 "3보다 크거나 같다"라는 value가 확보된 상태에서 chile node의 value가 "2"이니까 value가 2인 chile node는 더이상 펼쳐서 값을 계산할 필요가 없어졌다
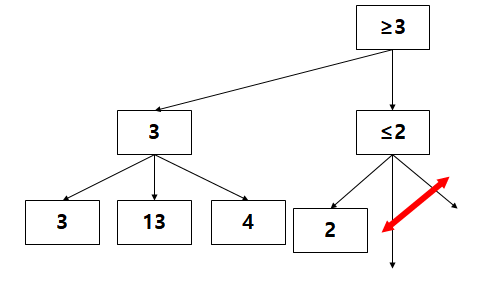
따라서 아직 값을 모르는 2개의 "?" node들을 "가지치기"함으로써 불필요한 계산을 하지 않게 설정해준다
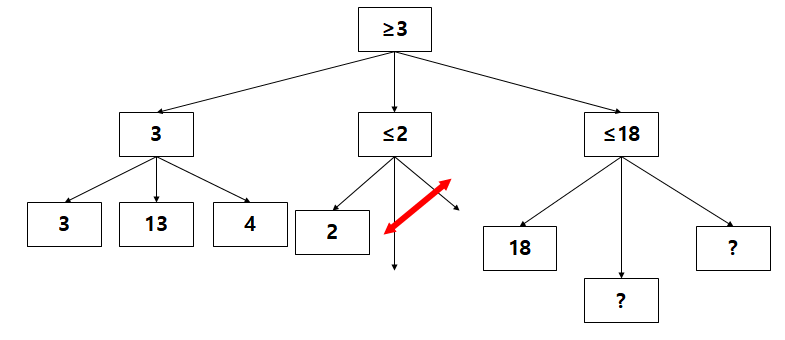
"최대 18"이라는 child node가 새롭게 설정이 되었지만 root node는 아직 해당 child node에 대한 모든 평가가 끝난게 아니기 때문에 자신의 bound value를 변경해주지 않는다
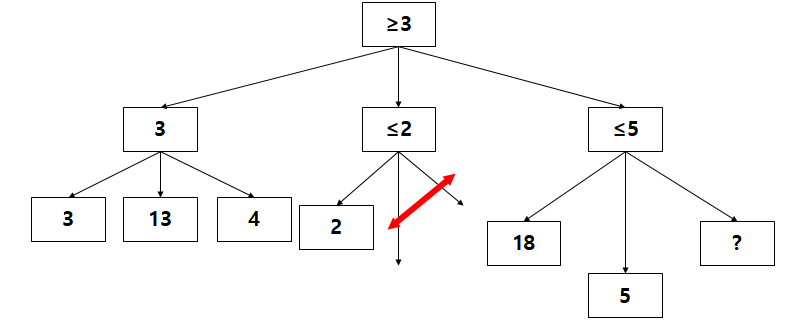
2개의 ? 중 하나가 5라는 사실이 밝혀짐에 따라서 해당 child node는 "최대 5의 value"를 보유하게 된다
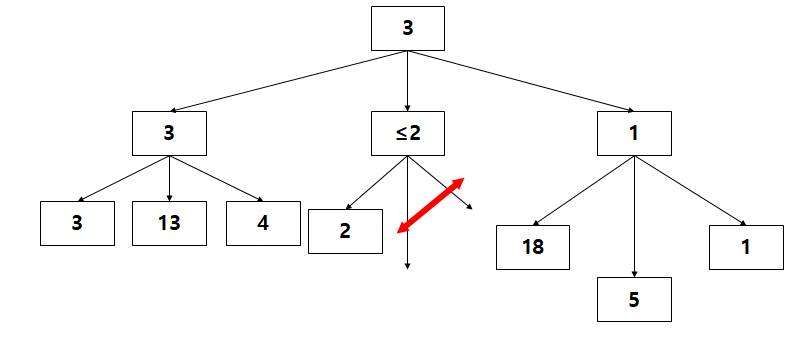
모든 node에 대한 평가가 끝남에 따라 root node의 value는 Math.max(3, ≤2, 1) = 3으로 결정되었다
α - β Pruning의 규칙
- MAX Line의 node value를 alpha(node)
- MIN Line의 node value를 beta(node)
1) 현재 Line = MAX
alpha(node) ≥ beta(ancestor)라면
→ node(현재 : alpha) branch를 잘라버리기 :: "α Cutoff"
2) 현재 Line = MIN
beta(node) ≤ alpha(ancestor)라면
→ node(현재 : beta) branch를 잘라버리기 :: "β Cutoff"
>> 이러한 규칙의 경우는 외울 필요가 없고 그냥 생각해보면 된다
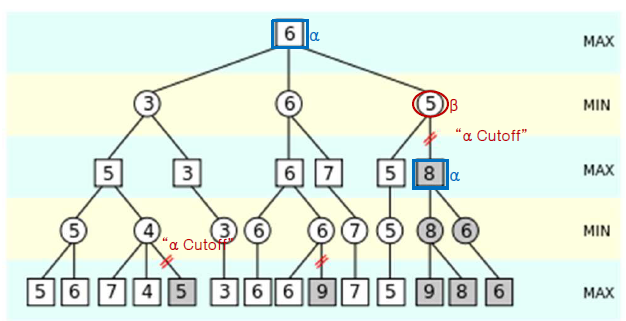
왼쪽의 value(4)인 노드를 보자
해당 node의 child value들을 보면 (7, 4, 5)이다
alpha(5)는 beta(4)보다 크기 때문에 alpha(5)의 branch는 잘라버려도 된다 :: "α Cutoff"
오른쪽의 value(5)인 노드를 보자
해당 node의 chile value를 보면 (5, 8)이다
alpha(8)은 beta(5)보다 크기 때문에 alpha(8)의 branch는 잘라버려도 된다 :: "α Cutoff"
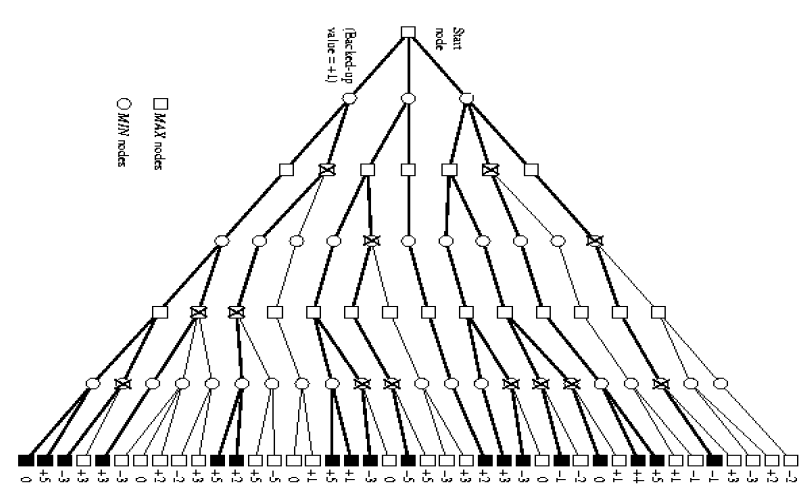


3) Negamax Algorithm
Minimax는 각 Line을 MAX/MIN으로 구분해서 해당 line의 node들의 value를 자식 node들의 value로부터 계산해서 구하였다
하지만 Negamax에서는 모든 Line을 MAX로 간주하고 계산한다
- 계산방법은 일반적으로 계산하는 것과는 다르게 계산한다
>> 계산방법은 child node들을 전부 Negation시킨 다음에 MAX 값을 찾는 것이다
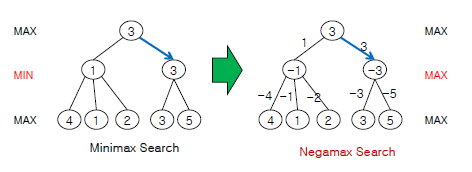

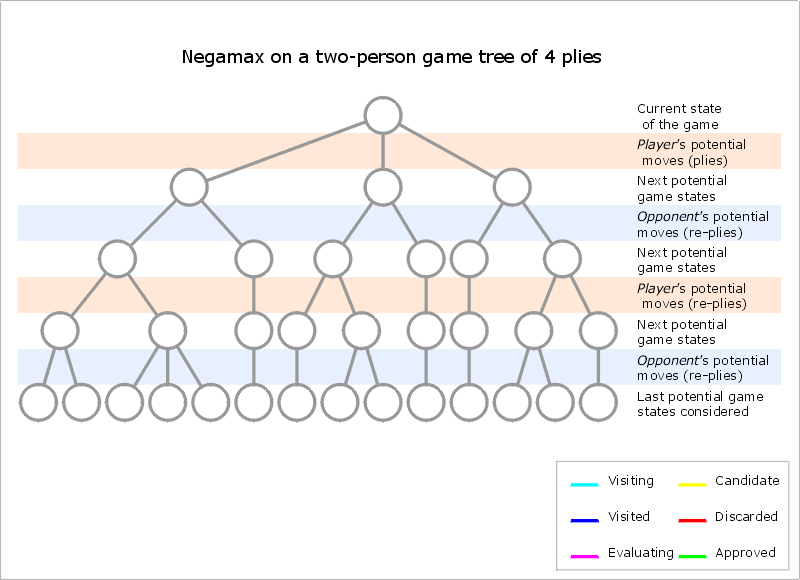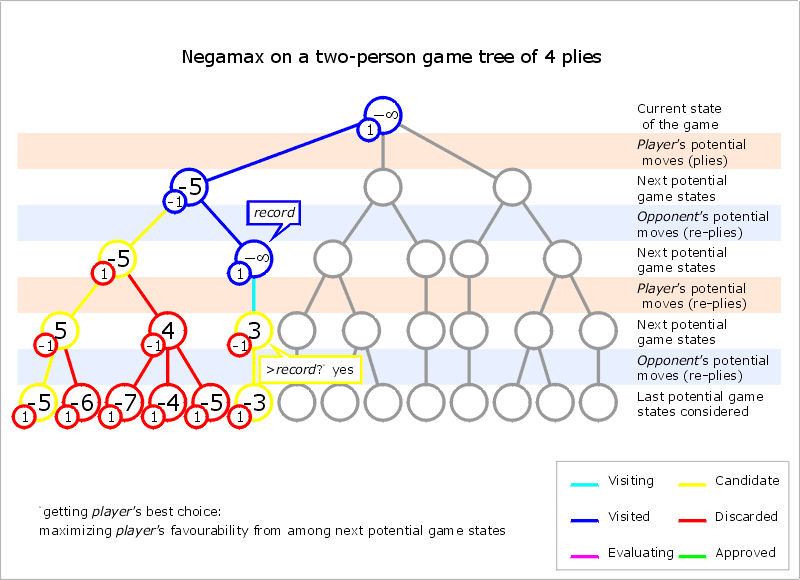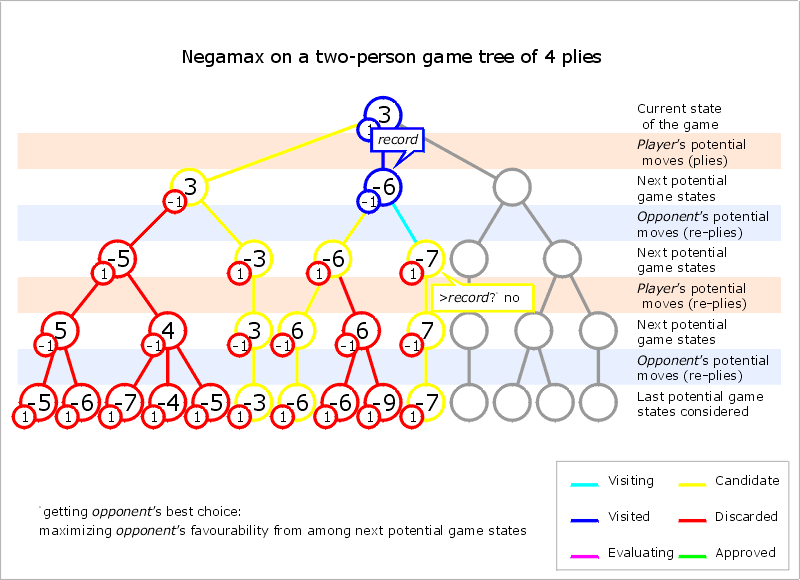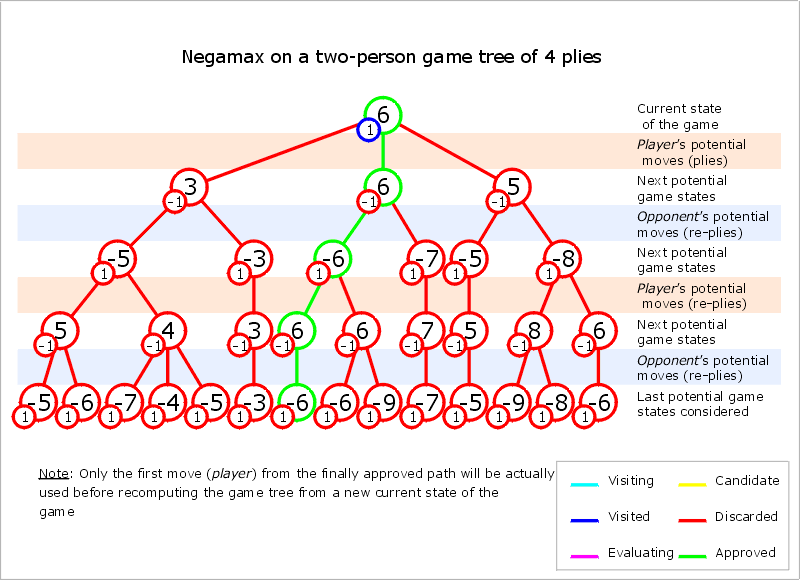
Line 2)
왼쪽 node부터 보자면 child node들의 value는 (4, 1, 2)이다
>> 여기서 child node들의 value를 Negation :: (-4, -1, -2)
따라서 왼쪽 node의 value는 Math.max(-4, -1, -2) = -1이 된다
오른쪽 node는 child node들의 value는 (3, 5)이다
(3, 5) →(Negation) :: (-3, -5)
따라서 오른쪽 node의 value는 Math.max(-3, -5) = -3이 된다
Line 1) root node
위에서 구한 Line 2)의 value는 (-1, -3)이 된다 :: (-1, -3) →(Negation) :: (1, 3)
따라서 root node의 value는 Math.max(1, 3) = 3이 된다