2022. 4. 16. 19:36ㆍMajor`/알고리즘
Backtracking
뜻 그대로 "가다가 막히면 왔던 길 다시 되돌아가기"이다
"Tries to construct a solution incrementally by a sequence of correct of best decisions"
단계를 하나하나씩 늘려가면서(incrementally) 우리가 원하는 결과에 대한 sequence를 생성해낸다
하지만 이 때 끝에 도달했는데 결과가 나오지않는다면 다시 "Backtracking"한다
어떠한 탐색이든지 root node가 존재할 것이고 이 root node로부터 Tree 형태로 탐색 범위를 확장시킬 것이다

여기서 이렇게 탐색을 이어나간다고 하자
결국 node로부터의 여러 child node가 존재하는데 "모든 갈림길을 평가 후 best node를 선택"하는 방식이다
- 모든 갈림길 :: Backtracking
- 평가 :: Recursively Evaluate

왼쪽 최하단까지 도달을 하였는데 우리가 원하는 Solution이 아니였다

왔던 곳을 다시 돌아가고(Backtracking) 다른 갈림길을 평가한다(Recursively Evaluate)
1) N Queens Problem


N x N 체스판이 존재한다
여기다가 N개의 Queen을 놓으려고 한다
>> 각 Queen들이 서로 공격을 하지 않도록 놓을 수 있는 방법은??
여러가지 방법이 존재하겠지만 여기서는 가장 대표적인 "Gauss's Recursive Strategy"를 적용해서 문제를 해결할 것이다
1. Queen을 위에서부터 각 row에 하나씩 배치
2. r번째 Queen을 r번째 row에 배치할 때 해당 row의 column 모두 시도해본다 (Backtracking)
- 만약 "임시로" 놓은 column(k)에 대해서 (0 ~ r-1)번째 퀸들에 의해서 공격을 받는다면 해당 column(k)는 무시
- 공격을 받지않는다면 일단 column(k)에 "임시로" 배치하고 r+1번째 Queen을 놓으려고 한다 (Recursion)
"임시로" 놓는 것이 가장 중요하다
왜냐하면 일단 "임시로" 놓았다가 조건에 만족되지 않으면 Backtracking을 해야하기 때문이다
NQueens_Solution(buffer, 0);
static void NQueens_Solution(int [] buffer, int r){
if(r == N){
count++;
System.out.println("## " + count + " ##");
Print_Queens(buffer);
System.out.println();
}
for(int i=0; i<N; i++){
boolean flag = true;
for(int j=0; j<r; j++){
if(buffer[j] == i || buffer[j] == i - (r - j) || buffer[j] == i + (r - j)){
flag = false;
break;
}
}
if(flag){
buffer[r] = i;
NQueens_Solution(buffer, r + 1);
}
}
}일반적으로 말을 하는거면 "첫번째 Queen을 놓겠습니다"가 가장 처음에 수행하는 일이지만
문제 풀이의 편리성을 위해서 여기서는 "0번째 Queen을 놓겠습니다"를 가장 처음에 수행하는 일이라고 하자
전체적으로 Recursion부터 보면
## N = 4 ##
NQueens_Solution(buffer, 0);
NQueens_Solution(buffer, 1);
NQueens_Solution(buffer, 2);
NQueens_Solution(buffer, 3);
NQueens_Solution(buffer, 4);
4 Queen이니까 Queen을 총 4번 놓고 (buffer, 3)에서 종료될 거 같지만 코드를 보게되면 (buffer, 3)전까지 (0 ~ 2)번째 Queen : 즉 3개의 Queen을 놓고 (buffer, 3)에서 마지막 Queen을 놓으니까 (buffer, 3)에서 함수를 return시키면 안되고 (buffer, 4)에서 즉시 return시켜야 한다
- (buffer, r)에서는 r번째 Queen을 "지금 놓는 것"이지 "이미 놓아진 것"이 아니다
따라서 index를 벗어난 (buffer, 4)를 호출하면 "Base Case"에 의해서 바로 Recursion이 종료되어야 한다
일단 함수의 파라미터부터 보면
NQueens_Solution(int [] buffer, int r)이 함수는 "r번째 Queen을 놓겠습니다"를 의미하는 함수이다
여기서 중요한 "buffer 배열"은 (0 ~ r-1)까지의 Queen들이 각 row의 어느 column에 있는지를 저장해놓은 배열이다
이제 세부적인 코드를 살펴보면
for(int i=0; i<N; i++)우리가 이 함수를 호출하는 목적은 "r번째 Queen 놓기"가 목적이다
따라서 r번째 Queen은 row(r)에서 column(0 ~ N-1)까지 놓을 수 있는 상황이다
따라서 모든 가능한 경우의 수를 검증(Backtracking)하면서 탐색을 진행해야 한다
▶ 변수 i는 한마디로 r번째 Queen이 column 어디에 놓일건가를 나타내는 변수이다
boolean flag = true;r번째 Queen을 그냥 row(r)의 모든 column에 놓을 수 있는 것은 아니다
"이전에 놓은 Queen들이 자신을 공격할 수 있을지"를 판단해서 놓아야 한다
▶ flag는 이전에 놓은 Queen들이 r번째 Queen을 공격할 수 있다면 "false"로 설정해주고 Backtracking해야 한다
for(int j=0; j<r; j++)이 for문에서는 (0 ~ r - 1)번째 Queen들의 위치와 r번째 Queen의 위치간에 서로 공격할 수 있을지 여부를 판단하는 단락이다
▶ j는 buffer[j]로 활용함으로써 (0 ~ r - 1) Queen들이 row(0) ~ row(r-1)에 각각 어디에 위치한지 check할 수 있다
if(buffer[j] == i || buffer[j] == i - (r - j) || buffer[j] == i + (r - j))이 조건을 하나하나 살펴보자
- j : (0 ~ r - 1)번째 Queen들
- buffer[j] : (0 ~ r - 1)번째 Queen들의 각각의 위치
- r : r번째 Queen
- i : r번째 Queen의 column 위치 → buffer[r]
1) buffer[j] == i
이 경우는 r번째 Queen이 (0 ~ r - 1) Queen들 중 몇몇에 의해서 "수직으로 공격"받는 상황이다

그림에서 보이는 것처럼 2번째 Queen에 의해서 r번째 Queen은 공격을 받고 있다
이러면 r번째 Queen은 해당 column에 놓지 못하기 때문에 Backtracking을 통해서 다른 갈림길을 평가해야 한다
2) buffer[j] == i - (r - j)
이 경우는 r번째 Queen이 (0 ~ r - 1) Queen들 중 몇몇에 의해서 "왼쪽 대각선 상에서 공격"받는 상황이다
여기서 "r - j"가 의미하는 바는 "r번째 Queen과 이전 Queen간의 차이"를 나타낸다

이걸 보게되면 r번째 Queen과 하나 차이나는 (r-1)번째 Queen은 둘 사이의 column차이가 1이면 대각선에 의해서 공격을 받게 된다
(r-2)번째 Queen은 column이 2가 차이나면 대각선에 의해 공격을 받게 된다
...
...
따라서 "i - (r - j)"가 의미하는 것은 "r번째 Queen의 column 값과 (0 ~ r - 1)번째 Queen들의 column값이 얼마나 차이가 나냐"를 뜻한다
3) buffer[j] == i + (r - j)
이 경우는 r번째 Queen이 (0 ~ r - 1) Queen들 중 몇몇에 의해서 "오른쪽 대각선 상에서 공격"받는 상황이다
>> i - (r - j)는 왼쪽 대각선을 check하고, i + (r - j)는 오른쪽 대각선을 check하는 것이다
if(flag){
buffer[r] = i;
NQueens_Solution(buffer, r + 1);
}buffer[r] = i를 먼저 보면 이전에 if조건에 의해서 break가 되지 않고 여기까지 왔다는 의미는 "r번째 Queen을 column(i)에 놓을 수 있다"라는 의미이다
따라서 r번째 Queen의 위치를 저장하는 buffer의 buffer[r]에 i를 저장한다
이후에는 r+1번째 Queen을 놓아야 한다
이 문제는 우리가 처음에 정의한 문제인 (x번째 Queen 놓기)의 Reduction이므로 Recursion으로 해결할 수 있다
N Queens Code (Java)
package Test_6;
/*
N x N 체스판이 존재
여기다가 Queen N개를 놓으려고 한다
>> 각 Queen들이 서로 공격하지 않도록 놓을 수 있는 경우의 수는??
*/
import java.util.*;
public class N_Queens {
static Scanner sc = new Scanner(System.in);
static int N;
static int count = 0; // N x N에서의 경우의 수
public static void main(String[] args) {
System.out.print("N : ");
N = sc.nextInt();
int [] buffer = new int[N];
System.out.println("────────────────────────────────────");
NQueens_Solution(buffer, 0);
/*
보통 일상적으로는 "첫번째 말을 놓기"가 일반적이지만
문제 해결의 편리성을 위해서 "0번째 말을 놓기"를 처음으로 가정
*/
System.out.println("────────────────────────────────────");
System.out.println("경우의 수 : " + count);
}
static void NQueens_Solution(int [] buffer, int r){
/*
buffer 배열 : (0 ~ r-1)번째 까지 Queen들이 어디에 놓여있는가를 저장하는 배열
r : NQueens_Solution에서 "r번째 Queen을 놓겠다"
*/
if(r == N){
/*
N개의 Queen들을 전부 놓았으면 놓아진 체스판 출력
*/
count++;
System.out.println("## " + count + " ##");
Print_Queens(buffer);
System.out.println();
}
for(int i=0; i<N; i++){
/*
i : r번째 퀸을 column(0) ~ column(N-1)중 어디에 놓을까를 결정
-> 일단 놓고 조건에 맞지 않으면 "Backtracking"
*/
boolean flag = true;
/*
일단 column(i)에 놓을 수 있다고 가정
>> 만약 어떠한 조건에 의해서 놓을 수 없다면 flag를 false로 설정
true일 경우에만 column(i)에 r번째 퀸 놓기
false면 "Backtracking"
*/
for(int j=0; j<r; j++){
/*
j : (0 ~ r-1)번째 퀸들이 현재 체스판의 어디에 놓여있는지 확인하기 위한 변수
*/
if(
buffer[j] == i // 이전 Queen들이 r번째 Queen바로 수직상에 존재
|| buffer[j] == i - (r - j) // 이전 Queen들이 r번째 Queen의 왼쪽 대각선에 존재
|| buffer[j] == i + (r - j) // 이전 Queen들이 r번째 Queen의 오른쪽 대각선에 존재
){
flag = false;
break; // 공격 받는다면 즉시 break걸고 "Backtracking"
}
}
if(flag){
buffer[r] = i; // "임시로" r번째 Queen은 column(i)에 놓기
NQueens_Solution(buffer, r + 1); // "r+1 Queen" 놓으러 가기 (Recursion)
}
}
}
static void Print_Queens(int [] buffer){
for(int i=0; i<buffer.length; i++){
for(int j=0; j<buffer.length; j++){
if(buffer[i] == j){
System.out.print("*");
}
else{
System.out.print("-");
}
}
System.out.println();
}
}
}


2) SubSetSum

어떤 집합 X가 존재한다
우리는 여기서 "집합의 원소들을 더해서 Target T가 되는 부분집합"을 찾고 싶다
## input ##
Set "X" & Target Num "K"
## output ##
Can Make? True? False?
X = {28, 93, 14, 2, 3, 7, 10, 5, 36}이 존재한다고 하자
우리는 Target Num을 57로 정하고 배열의 원소들을 더해서 57을 만들 수 있는지 없는지를 알고 싶다
물론 여러가지 방법이 있겠지만
가장 쉬운 방법은 집합에서 원소 하나하나를 선택하면서 "해당 원소를 포함해서 만들지 제외하고 만들지"만 고민하면 된다
→ 만약 포함한다면 집합의 남은 원소들 중에서 "K - value"를 만들면 된다
→ 만약 포함하지 않는다면 집합의 남은 원소들 중에서 "K"를 만들면 된다
SubSetSum Code (Java)
package Test_6;
/*
## input ##
1) 배열 A
2) 목표 숫자 T
>> 배열 A의 원소들을 어떻게 더하든 상관없이 T를 만들어낼수 있느냐
## output ##
True? False?
*/
public class SubSetSum {
public static void main(String[] args) {
int [] list = new int[10];
createElement(list);
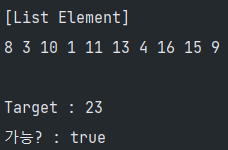
print_list(list, "[List Element]");
int target = (int)(Math.random()*100);
System.out.println("Target : " + target);
System.out.println("가능? : " + SubSetSum_Solution(list, list.length - 1, target));
}
static boolean SubSetSum_Solution(int [] list, int index, int target){
/*
당연히 원소들을 list로부터 뽑아서 target을 만들려고 한다
>> 여기서 원소를 select하는 개념
## list["마지막 원소"]부터 차레대로 뽑기 ##
-> 뽑은 원소를 target을 만들어가는 과정에 포함시키기 -- (1)
-> 뽑은 원소를 target을 만들어가는 과정에 포함시키지 않기 -- (2)
>> Recursion
Result : (1) | (2)
-> 어차피 갈림길이 2가지이므로 어느 갈림길 중에서 하나가 target을 만들 수 있다면 전체적으로 보면 True
*/
if(target == 0){
return true;
}
else if(target < 0 || index == 0){
/*
(1) Recursion을 통해서 target을 만들어가는데 target이 음수 :: 못만듦
(2) index가 배열의 첫번째에 도달했는데 target 못만듦
*/
return false;
}
else{
int value = list[index]; // index번째 원소 생각
boolean with = SubSetSum_Solution(list, index - 1, target - value); // value 포함
boolean wout = SubSetSum_Solution(list, index - 1, target); // value 미포함
return with | wout;
}
}
static void createElement(int [] list){
for(int i=0; i<list.length; i++){
list[i] = (int)(Math.random()*20);
for(int j=0; j<i; j++){
if(list[j] == list[i]){
i--;
break;
}
}
}
}
static void print_list(int [] list, String s){
System.out.println(s);
for(int i=0; i<list.length; i++){
if (i%10 == 0 && i != 0){
System.out.println();
}
System.out.print(list[i] + " ");
}
System.out.println("\n");
}
}


SubSetSum 문제를 변형시켜서 단순히 가능/불가능만 표현하는게 아니라 가능하다면 어떠한 SubSet이 도출되고 그 경우의 수는 몇가지인지도 알 수 있다
package Test_6;
/*
SubSetSum 변형 1) "합이 T인 SubSet을 (모두? 하나만?) 출력
*/
import java.util.ArrayList;
import java.util.Scanner;
public class SubSetSum_Print {
static Scanner sc = new Scanner(System.in);
static StringBuilder sb = new StringBuilder(); // SubSet 저장 전용 StringBuilder
static int count = 0;
public static void main(String[] args) {
int [] list = new int[10];
createElement(list);
print_list(list, "[List Element]");
int target = (int)(Math.random()*100);
System.out.println("Target : " + target);
System.out.println("────────────────────────────────────");
ArrayList<Integer> buffer = new ArrayList<>(); // SubSet
SubSetPrint(list, list.length - 1, target, buffer);
if(sb.length() > 0){
System.out.println("## SubSet 존재 O ##");
System.out.print(sb);
}
else{
System.out.println("## SubSet 존재 X ##");
}
System.out.println("\n총 경우의 수 : " + count);
}
static void SubSetPrint(int [] list, int index, int target, ArrayList<Integer> buffer){
if(target == 0){
count++;
StringBuilder s = new StringBuilder();
for(Integer n : buffer){
s.append(n).append(" ");
}
sb.append(s).append("\n");
return;
}
else if(target < 0 || index == 0){
return;
}
else{
int value = list[index];
ArrayList<Integer> buffer_plus = new ArrayList<>(buffer);
buffer_plus.add(value);
SubSetPrint(list, index - 1, target - value, buffer_plus);
SubSetPrint(list, index - 1, target, buffer);
}
}
static void createElement(int [] list){
for(int i=0; i<list.length; i++){
list[i] = (int)(Math.random()*20);
for(int j=0; j<i; j++){
if(list[j] == list[i]){
i--;
break;
}
}
}
}
static void print_list(int [] list, String s){
System.out.println(s);
for(int i=0; i<list.length; i++){
if (i%10 == 0 && i != 0){
System.out.println();
}
System.out.print(list[i] + " ");
}
System.out.println("\n");
}
}


LIS : Longest Increasing Subsequence
먼저 Sequence는 "원소들이 순서를 가지고 나열된 것"이다
SubSequence는 Sequence S에서 "0개 이상의 원소들을 삭제"해서 얻을 수 있는 Sequence이다
>> 따라서 Subsequence는 반드시 Sequence에서 연속적인 집합이 아니라 불연속이여도 된다
Example) Sequence : {8, 2, 7, 4}
Subsequence는 무엇일까?
{}, {8}, {2}, {7}, {4} {8, 2}, {8, 7}, {8, 4}, {2, 9}, {2, 4}, {9, 4}, {8, 2, 9}, {8, 2, 4}, {8, 9, 4}, {2, 9, 4}, {8, 2, 9, 4}
>> 총 16개로써 2원소 개수의 경우의 수가 존재한다
이 예제만 봐도 Subsequence는 Sequence로부터 연속이 아니여도 상관이 없다
이제 LIS의 의미를 파악하자면 LIS는 "Subsequence중 원소의 value가 계속 증가하는 Subsequence들 중 길이가 가장 긴 Subsequence"를 말한다
이러면 위에서 LIS는 {}, {8}, {2}, {7}, {4}, {2, 9}, {2, 4} >> 따라서 LIS는 "2"이다
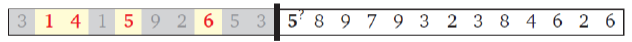
검은 선 왼쪽은 이미 탐색을 통해서 정했다고 가정하자
이러면 우리는 다음 수인 5를 포함할지 말지를 결정해야 한다
당연히 이전에 탐색한 가장 큰 값인 6보다 5가 작기 때문에 추가하지 않고 넘어간다

그러면 8은 어떻게 정해줘야 할까??
무조건 추가? skip?
"이 때 두가지의 경우의 수를 모두 판단해서 결론적으로 LIS를 고려해서 선택해줘야 한다"
>> "임시로" 8을 포함하고 나머지 결정 Recursion
>> "임시로" 8을 제외하고 나머지 결정 Recursion
이러한 방식은 위의 사진의 "첫번째 방식"으로 해결하는 구조이다

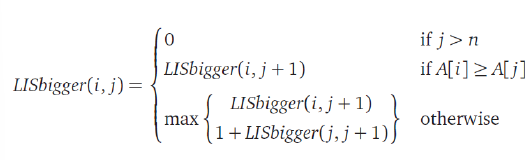
"두 번째 방식"은 어떻게 해결할까??

아까는 이 상태에서 "5"만을 생각해서 5를 포함할지 제외할지 결정했다면
"두 번째 방식"은 6 이후의 값들 중에서 가능한 값들을 먼저 추린다

이제 {8, 9, 7, 9, 8}을 다 고려해서(Backtracking) 하나하나 경우를 보면 된다

각각의 경우를 따져보고 best case를 최종적으로 선택한다


첫번째 & 두번째 방식의 공통점은 무엇일까
결론적으로 "가장 최근에 선택한 값"을 둘다 기억하고 있다는 것이다
LIS Code (Java)
package Test_6;
/*
## input ##
배열 A
## output ##
배열 A에서 증가하는 Sequence중에서 가장 긴 Sequence의 길이
-> SubSequence는 오른쪽으로 갈 수록 계속 증가하는 숫자들만 있어야 한다
여기서 SubSequence는 Sequence에서 연속적인 것이 아니라
>> "Sequence에서 숫자들을 삭제함으로써 얻어진다"
따라서 SubSequence는 원래 Sequence에서 연속이 아니여도 된다
*/
public class LIS {
public static void main(String[] args) {
int [] list = new int[20];
createElement(list);
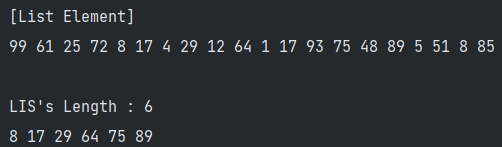
print_list(list, "[List Element]");
System.out.println("LIS's Length : " + LIS_Solution(list, 0, 0));
}
static int LIS_Solution(int [] list, int index, int preValue){
/*
index : list에서의 각 index
preValue : 이전 Recursion에서 선택했던 list의 Value
*/
if(index == list.length){
return 0;
}
else if(list[index] <= preValue){
return LIS_Solution(list, index + 1, preValue);
}
else{
/*
여기 단락에서 list[index]는 preValue보다 크다
>> 이제 list[index]를 포함할거냐 포함안하고 다음으로 넘어갈거냐
*/
int with = LIS_Solution(list, index + 1, list[index]) + 1;
// "+ 1"은 list[index]를 포함하기 때문에 LIS의 길이가 1 증가
int wout = LIS_Solution(list, index + 1, preValue);
/*
결국 이 메소드는 LIS의 "길이"를 구하기 때문에 with & wout중 긴거를 최종적으로 return
*/
return Math.max(with, wout);
}
}
static void createElement(int [] list){
for(int i=0; i<list.length; i++){
list[i] = (int)(Math.random()*100);
}
}
static void print_list(int [] list, String s){
System.out.println(s);
for (int j : list) {
System.out.print(j + " ");
}
System.out.println("\n");
}
}
LIS도 물론 가장 긴 Subsequence의 길이만 구하는 것이 아니라 문제를 변경한다면 가장 긴 Subsequence를 출력할 수 있다
package Test_6;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class LIS_Print {
static ArrayList<Integer> result = new ArrayList<>();
public static void main(String[] args) {
int [] list = new int[20];
createElement(list);
print_list(list, "[List Element]");
ArrayList<Integer> buffer = new ArrayList<>();
int resultLength = LIS_Solution(list, 0, 0, buffer);
System.out.println("LIS's Length : " + resultLength);
ArrayListPrint(result);
}
static int LIS_Solution(int [] list, int index, int preValue, ArrayList<Integer> buffer){
if(index == list.length){
if(result.size() < buffer.size()){
result = buffer;
}
return result.size();
}
else if(list[index] <= preValue){
return LIS_Solution(list, index + 1, preValue, buffer);
}
else{
ArrayList<Integer> buffer_plus = new ArrayList<>(buffer);
buffer_plus.add(list[index]);
int with = LIS_Solution(list, index + 1, list[index], buffer_plus);
int wout = LIS_Solution(list, index + 1, preValue, buffer);
return Math.max(with, wout);
}
}
static void ArrayListPrint(ArrayList<Integer> result){
for(Integer n : result){
System.out.print(n + " ");
}
}
static void createElement(int [] list){
for(int i=0; i<list.length; i++){
list[i] = (int)(Math.random()*100);
}
}
static void print_list(int [] list, String s){
System.out.println(s);
for (int j : list) {
System.out.print(j + " ");
}
System.out.println("\n");
}
}