2022. 2. 2. 18:30ㆍMajor`/컴퓨터구조
산술논리연산장치 (ALU : Arithmetic and Logical Unit)
- CPU 내부 구성 요소들 중 하나
- 수치/논리 Data에 대해서 실질적으로 연산을 수행하는 하드웨어 모듈
- 산술적 계산 : 정수(Integer) / 부동소수점 수(Floating-Point Number) 2가지 형태의 수들에 대해 수행
- 논리적 계산 : 0, 1의 배열로 표현되는 2진 데이터(binary data)에 대해 수행
ALU 구성요소

산술 연산장치
- 산술 연산(+ / - / × / ÷)을 수행
논리 연산장치
- 논리 연산(AND / OR / XOR / NOT,...)을 수행
보수기 (Complementer)
- Data에 대해서 2의 보수를 취한다
- Data를 음수로 만든다
시프트 레지스터 (Shift Register)
- bit들을 좌측/우측으로 이동시킨다
상태 레지스터 (Status Register)
- 연산 결과의 상태를 나타내는 플래그(flag)들을 저장
- 플래그들은 조건 분기 명령어 or 산술 명령어들에 의해 사용된다
소수 표현
| 2진수 | 1101.101 | |||||||
| 자릿수 | 2³ | 2² | 2¹ | 20 | 0 | 2-1 | 2-2 | 2-3 |
| 10진수 변환 |
1 × 2³ | 1 × 2² | 0 × 2¹ | 1 × 20 | 0 | 1 × 2-1 | 0 × 2-2 | 1 × 2-3 |
| 최종 10진수 | 8 + 4 + 1 + 0.5 + 0.125 = 13.625 | |||||||
음수 표현
(1) 부호화-크기 표현
- 3개의 표현방법 중 가장 간단한 방법
- 단어의 bit 수 : n개
- 맨 좌측 bit = 부호 비트
- 나머지 (n-1)개의 bit = 수의 크기
>## 8-bit 정수들에 대한 부호화-크기 표현 ##
1) +9 : 0 0001001
2) -9 : 1 0001001
3) +35 : 0 0100011
4) -35 : 1 0100011
▶ 문제점
1. 덧셈/뺄셈을 수행하려면 (부호 비트, 크기 비트)를 별도로 처리해야 한다
2. 0에 대한 표현이 2가지이다
- 0 0000000 = +0
- 1 0000000 = -0
- → Data가 '0'인지 검사하는 과정이 복잡해진다
- → n-bit 2진수로 표현할 수 있는 수들이 (2ⁿ-1)개로 줄어든다
≫ 이러한 문제점들을 해결 : 보수 표현
- 양수는 부호화-크기 표현, 보수 표현은 서로 동일하다
- 음수의 경우 부호화-크기 표현, 보수 표현은 서로 다르다
(2) 1의 보수 표현
- 모든 bit들을 reverse (0 → 1 / 1 → 0)
- n-bit 수 표현 범위 : -(2n-1 - 1) ~ (2n-1 - 1)
- '0'에 대한 표현이 2가지이기 때문에 2의 보수 표현보다 범위가 하나 작다
(3) 2의 보수 표현
- 모든 bit들을 reverse하고 1을 더해준다
- n-bit 수 표현 범위 : -2n-1 ~ (2n-1 - 1)
- 거의 모든 컴퓨터에서 2의 보수 표현을 사용한다
## 2의 보수 -> 10진수 변환 ##
1. 맨 좌측 bit가 0 (양수)인 경우
-> 맨 좌측 bit를 제외한 나머지 bit들에 대해 각 자릿수를 곱해서 계산
ex) 01110001 -> 2^(0) + 2^(4) + 2^(5) + 2^(6) = 113
2. 맨 좌측 bit가 1 (음수)인 경우
-> 맨 좌측 bit를 2의 제곱수로 만들고 나머지 bit들은 각 자릿수를 곱해서 계산
ex) 11110001 -> -2^(7) + (2^(0) + 2^(4) + 2^(5) + 2^(6)) = -128 + 113 = -15부호-비트 확장
기억장치에 저장되어 있는 수의 길이와 CPU 연산 과정에서의 길이가 서로 다른 경우가 있다
- 기억장치에 8-bit로 저장되어 있는 Data >> 16-bit 레지스터에 저장하는 경우
- 부호 비트는 무조건 맨 좌측에 위치하고, 나머지 빈공간들은 0으로 채워주면 된다
8-bit 부호화 크기 표현 (+21)
>> 00010101
============================
16-bit 부호화 크기 표현 (+21)
>> 0000000000010101
-----------------------------
8-bit 부호화 크기 표현 (-21)
>> 10010101
============================
16-bit 부호화-크기 표현 (-21)
>> 1000000000010101
2의 보수인 경우
- 확장되는 상위 bit들은 반드시 부호 비트와 동일한 값으로 설정해야 한다
- 양수 : 확장되는 상위 bit들을 전부 0으로 설정
- 음수 : 확장되는 상위 bit들을 전부 1로 설정
8-bit 2의 보수 (+21)
>> 00010101
=====================
16-bit 2의 보수 (+21)
>> 0000000000010101
---------------------
8-bit 2의 보수 (-21)
>> 11101011
=====================
16-bit 2의 보수 (-21)
>> 1111111111101011논리 연산
- 숫자 Data들은 컴퓨터에서 word단위로 취급된다
- 논리 연산은 word 내의 각 bit단위로 연산이 처리된다
| 기본적인 논리 연산 |
||||||
| A | B | NOT A | NOT B | A AND B | A OR B | A XOR B |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
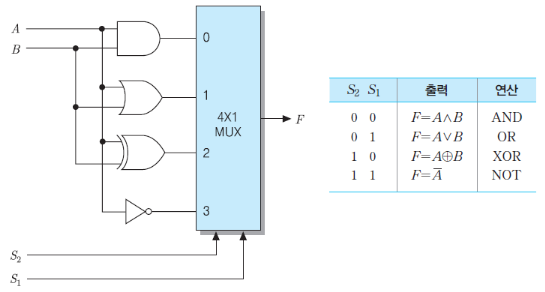
1. 입력 bit들은 모든 게이트들을 통과 → 각 논리 연산의 출력 발생
2. 2개의 선택 신호들(S1, S2)에 의해 선택된 연산의 출력만 멀티플렉서의 4가지 입력들 중에 하나를 출력
>> S1, S2가 어떤 값이 입력되냐에 따라 AND / OR / XOR / NOT중 하나가 결정
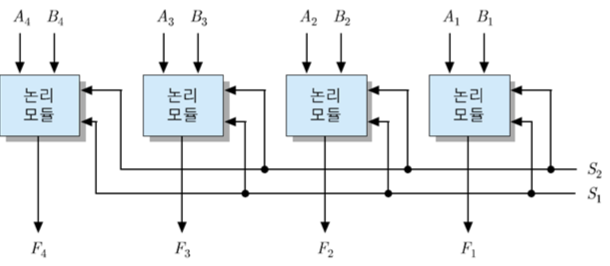
- 논리 연산에서는 대응되는 bit들 간에 독립적으로 연산 수행
- 모듈간의 Data 전송 통로가 필요없다
AND 연산
- 두 bit가 모두 1이면 1로 설정
| A | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| B | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| A AND B | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
OR 연산
- 두 bit중 하나만 1이여도 1로 설정
| A | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| B | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| A OR B | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
XOR 연산
- 두 bit가 서로 동일하면 0으로 설정
- 두 bit가 서로 다르면 1로 설정
| A | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| B | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| A XOR B | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
NOT 연산
- 해당 Data의 모든 비트들을 reverse시킨다
| A | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| NOT A | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
선택적-세트 연산
- Data의 특정 bit들을 1로 설정해주기 위한 연산
- Data가 저장된 A 레지스터 / 설정할 bit들의 위치를 지정해주는 B 레지스터
- OR 연산 수행
- B 레지스터에서 값이 1인 bit >> A 레지스터도 해당 위치의 bit가 1이 된다
- B 레지스터는 A 레지스터에서 1로 설정할 bit의 위치를 1로 설정하면 된다
Example) A 레지스터 (10010010)의 하위 5bit를 1로 설정
- B 레지스터의 하위 5bit를 1로 설정하고 / 나머지 bit들은 0으로 설정
- A, B 간에 OR 연산을 수행하면 된다
| A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| B | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 선택적-세트 >> OR 연산 |
1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
선택적-보수 연산
- Data의 특정 bit들을 reverse시키기 위한 연산
- Data가 저장된 A 레지스터 / reverse시킬 bit들의 위치를 지정해주는 B 레지스터
- XOR 연산 수행
- B 레지스터에서 값이 1인 bit >> A 레지스터의 해당 위치의 bit는 reverse
- B 레지스터는 A 레지스터에서 reverse할 bit의 위치를 1로 설정하면 된다
Example) A 레지스터 (10010010)의 하위 5bit를 reverse
- B 레지스터의 하위 5bit를 1로 설정하고 / 나머지 bit들은 0으로 설정
- A, B 간에 XOR 연산을 수행하면 된다
| A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| B | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 선택적-보수 >> XOR 연산 |
1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
마스크 연산
- 선택적-세트 연산과 반대로 연산
- Data의 특정 bit들을 0로 설정해주기 위한 연산
- Data가 저장된 A 레지스터 / 설정할 bit들의 위치를 지정해주는 B 레지스터
- AND 연산 수행
- B 레지스터에서 값이 0인 bit >> A 레지스터도 해당 위치의 bit가 0이 된다
- B 레지스터는 A 레지스터에서 0으로 설정할 bit의 위치를 0으로 설정하면 된다
Example) A 레지스터 (10010010)의 하위 5bit를 0로 설정
- B 레지스터의 하위 5bit를 0로 설정하고 / 나머지 bit들은 1로 설정
- A, B 간에 AND 연산을 수행하면 된다
| A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| B | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 마스크 연산 >> AND 연산 |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
삽입 연산
1. 마스크 연산 수행 -- (1) >> 삽입할 자리의 bit들을 전부 0으로 reset하는 과정
2. 새로 삽입할 bit들과 (1)의 결과 간에 OR 연산 수행
Example) A 레지스터 (10010010)의 상위 4bit를 '1110'으로 변경
- B 레지스터를 00001111로 설정 후, A 레지스터와 마스크 연산(AND 연산) -- (1)
- (1)의 결과와 삽입할 bit "11100000" 간에 OR 연산 수행
| A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| B | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 마스크 연산 >> AND 연산 |
0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 삽입할 bit | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| result >> OR 연산 |
1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
비교 연산
- A, B 레지스터의 bit들을 비교해서
- 만약 대응되는 bit들의 값이 동일하면 A 레지스터의 해당 bit들을 0으로 설정
- XOR 연산 수행
| A | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| B | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| A XOR B | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
논리적 시프트 연산
- 레지스터 내의 Data bit들을 좌/우로 1칸씩 이동시키는 연산
논리적 좌측-시프트
- 좌측-시프트 연산을 1번 수행하면 원래 수 × 2 결과가 된다
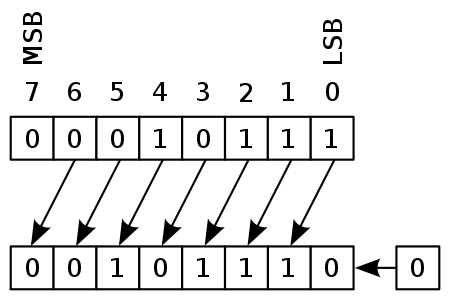
1. 최상위 bit는 버리기
2. 나머지 bit들은 전부 왼쪽으로 1칸씩 이동
3. 최하위 bit에는 0 설정
논리적 우측-시프트
- 우측-시프트 연산을 1번 수행하면 원래 수 ÷ 2 결과가 된다
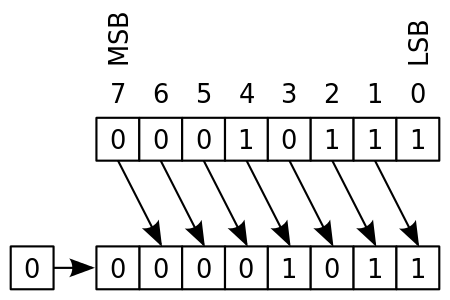
1. 최상위 bit에는 0 설정
2. 나머지 bit들은 전부 오른쪽으로 1칸씩 이동
3. 최하위 bit는 버리기
순환 시프트 연산
- 논리적 시프트와 비슷하지만 but
- bit들을 버리지 않고, 반대편 끝에 넣어두기
순환 좌측-시프트
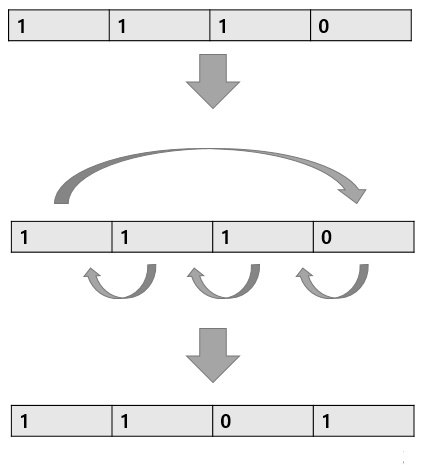
1. 최상위 bit를 꺼내서 보관
2. 나머지 bit들은 왼쪽으로 1칸씩 이동
3. 보관된 최상위 bit를 최하위 bit에 넣어두기
순환 우측-시프트
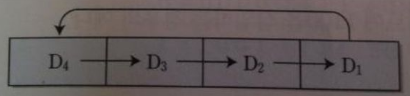
1. 최하위 bit를 꺼내서 보관
2. 나머지 bit들은 오른쪽으로 1칸씩 이동
3. 보관된 최하위 bit를 최상위 bit에 넣어두기
직렬 Data 전송 (Serial Data Transfer)
- 논리적 시프트 연산 + 순환 시프트 연산
- 하나의 레지스터 bit들을 또 다른 하나의 레지스터로 전부 옮기기 위해 수행
- A 레지스터의 Data를 B 레지스터로 전부 이동
- 보내는 곳 : 순환 시프트 연산
- 받는 곳 : 논리적 시프트 연산
- A 레지스터는 Data를 전부 보내도 본인의 Data는 원래 것 그대로 유지된다
- Data의 bit 수만큼 클록주기가 반복된다
- A 레지스터는 각 클록주기마다 1번씩 순환 시프트 연산 수행
- B 레지스터는 각 클록주기마다 1번씩 논리적 리스트 연산 수행
Example) A 레지스터의 '1011'을 B 레지스터로 옮기기
- A 레지스터 : 순환 우측-시프트
- B 레지스터 : 논리적 우측-시프트
| A₄ | A₃ | A₂ | A₁ | B₄ | B₃ | B₂ | B₁ | |
| 초기상태 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| t(1) | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| t(2) | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| t(3) | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| t(4) | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
산술적 시프트 연산
- Data가 부호 비트를 가진 정수일 경우
- 부호 비트를 고려해서 시프트 수행
- 부호 비트 : 그대로 놔둔다
- 나머지 크기 비트 : 부호 비트빼고 나머지 크기 비트들만 시프트
※ 논리 시프트와의 차이
- 논리 시프트 : 부호비트가 보존 X
- 산술 시프트 : 부호비트가 보존 O
산술적 좌측-시프트
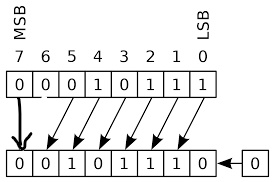
1. 부호 비트는 그대로 고정
2. 나머지 크기 bit는 왼쪽으로 1칸씩 이동 >> 크기 비트중 가장 왼쪽에 있는 bit는 없어진다
3. 최하위 bit는 0으로 설정
산술적 우측-시프트
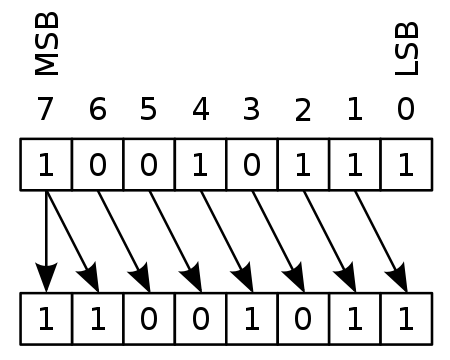
1. 부호 비트는 그대로 고정
2. 나머지 크기 bit는 오른쪽으로 1칸씩 이동 >> 크기 비트중 가장 왼쪽에 있는 bit는 부호 비트 값을 그대로 가져온다
C 플래그를 포함한 시프트 연산
- 실제 CPU에서는 시프트 연산에 올림수 플래그(C)가 포함
C 플래그를 포함한 좌측-시프트 (SHLC : Shift Left with Carry)
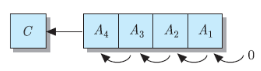
1. 최상위 비트가 C 플래그에 저장
2. 나머지 bit들은 왼쪽으로 1칸씩 이동
3. 최하위 bit는 0으로 설정
C 플래그를 포함한 우측-시프트 (SHRC : Shift Right with Carry)
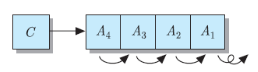
1. 최상위 비트은 C 플래그의 값으로 설정
2. 나머지 bit들은 오른쪽으로 1칸씩 이동
3. 최하위 bit는 버린다
C 플래그를 포함한 좌측 순환-시프트 (RLC : Rotate Left with Carry)
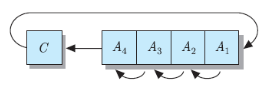
1. 최상위 비트는 C 플래그에 저장
2. 나머지 bit들은 왼쪽으로 1칸씩 이동
3. 최하위 bit는 C 플래그에 원래 저장되어 있던 값으로 설정
C 플래그를 포함한 우측 순환-시프트 (RRC : Rotate Right with Carry)
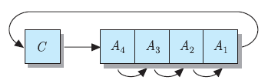
1. 최상위 비트는 C 플래그의 원래 값으로 설정
2. 나머지 bit들은 오른쪽으로 1칸씩 이동
3. 최하위 bit는 C 플래그에 저장
정수의 산술 연산
| 기본적인 산술 연산 :: 마이크로-연산 |
|
| 보수화 (2의 보수 변환) | |
| 덧셈 | |
| 뺄셈 | |
| 곱셈 | |
| 나눗셈 | |
| 증가 (Increment) | |
| 감소 (Decrement) | |
덧셈
1. 먼저 두 수를 더하기
2. 올림수(carry)가 발생하면 올림수는 버리기
병렬 가산기(Parallel Adder)

- 덧셈을 수행하는 하드웨어
- 전가산기(Full-Adder)가 데이터의 bit수만큼 존재
- 덧셈 연산 결과에 따라 해당 조건 플래그(Condition Flags)들을 설정
- C 플래그 : 올림수(carry) >> 올림수가 발생하면 해당 올림수로 설정
- S 플래그 : 부호(sign) >> 양수면 0, 음수면 1로 설정
- Z 플래그 : 0(zero) >> 합의 모든 bit들이 0이면 1로 설정
- V 플래그 : 오버플로우(Overflow) >> 오버플로우가 발생하면 1로 설정
캐리 / 오버플로우
▶ 캐리 (Carry)
- 최상위 bit(MSB)에서 자리 올림이 발생하는 것
ex) 1 + (-1)
- 0000 0001 + 1111 1111 = 1 0000 0000
- MSB에서 carry(1) 발생
- 이 carry는 어차피 버려진다
>> carry 자체로는 오류 발생과 관련 X
▶ 오버플로우 (Overflow)
- 연산 결과값이 Data의 표현범위를 넘어간 경우
ex)1 + 127
- 0000 0001 + 0111 1111 = 1000 0000
- 이 연산의 결과는 -128
- 8-bit Data의 표현범위는 -128 ~ 127이고, 원래 연산의 결과는 128이므로 오버플로우 발생
▶ 오버플로우 판단

- C1 : MSB 전 bit에서 MSB로의 올림수
- C2 : MSB에서 발생한 올림수 = carry
- C1, C2가 서로 값이 다르면 오버플로우 발생
| 수식 | 연산 과정 | 오버플로우 여부 |
| 1 + 1 = 2 |  |
C1 : 0 C2 : 0 >> 오버플로우 X |
| 1 + 127 = 128 |  |
C1 : 0 C2 : 1 >> 오버플로우 O |
| -128 + (-128) = -256 |  |
C1 : 0 C2 : 1 >> 오버플로우 O |
| 1 + (-1) = 0 |  |
C1 : 1 C2 : 1 >> 오버플로우 X |
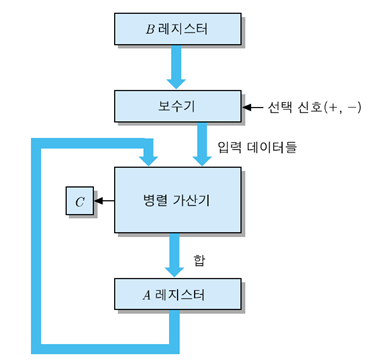
뺄셈
- 뺄셈을 덧셈으로 변경해서 계산해야 한다
- A : 피감수(Minuend) / B : 감수(Subtrahend)
- A - (+B) = A + (-B)
- A - (-B) = A + (+B)
1. A 레지스터의 Data는 바로 병렬 가산기에 입력된다
2. B 레지스터의 Data는 보수기를 통해서 병렬 가신기에 입력된다 (보수기를 통해서 해당 Data를 보수화)
곱셈
부호 없는 정수 곱셈
- A × B : 피승수 = A, 승수 = B
- 피승수에 승수의 최하위 bit부터 하나하나씩 곱한 값들 : 부분 적
- 부분 적들의 합 = 최종 결과
- 승수의 특정 bit가 1 : 부분 적 = 피승수
- 승수의 특정 bit가 0 : 부분 적 = 0

- 두 개의 n-bit 정수들의 곱 >> 결과값의 길이 = 최대 2n bit
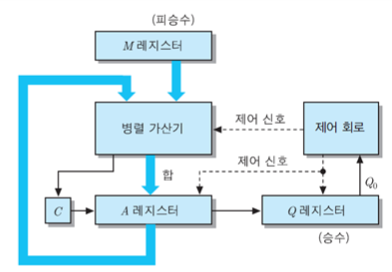
- M 레지스터 : 피승수 저장
- Q 레지스터 : 승수 저장
- A 레지스터, C플래그 : 초기에 전부 0으로 초기화
- 결과값은 A 레지스터(상위 bit), Q 레지스터(하위 bit)에 저장된다
1. Q 레지스터에 저장된 승수의 최하위 bit부터 검사 >> 해당 bit는 제어 회로로 입력된다
2. 제어 회로는 해당 bit를 검사한다 :: 1 = 덧셈 + 시프트 / 0 = 시프트
- 덧셈 : A + M -> A
- 시프트 : C → A → Q
## 1101 X 1011 (13 X 11) ##
>> 피승수 = 1101
>> 승수 = 1011
>> C플래그에는 올림수 저장
-------------------------------------------------------------
t(0) >> 초기상태
M 레지스터 : 1101
Q 레지스터 : 1011
A 레지스터 : 0000
C 플래그 : 0
-------------------------------------------------------------
이제 Q 레지스터(승수)의 최하위 bit부터 차례대로 검사
-------------------------------------------------------------
t(1) >> bit : 1검사
-> 1이므로 덧셈 + 시프트 연산 수행
(1) 덧셈 >> A + M -> A : 0000 + 1101 = 1101
M 레지스터 : 1101
Q 레지스터 : 1011
A 레지스터 : 1101
C 플래그 : 0
(2) 시프트 >> C->A->Q : 0 1101 1011 : 1 0110 1101
M 레지스터 : 1101
Q 레지스터 : 1101
A 레지스터 : 0110
C 플래그 : 0
-------------------------------------------------------------
t(2) >> bit : 1검사
-> 1이므로 덧셈 + 시프트 연산 수행
(1) 덧셈 >> A + M -> A : 0110 + 1101 = 0011 (carry 1 발생)
M 레지스터 : 1101
Q 레지스터 : 1101
A 레지스터 : 0011
C 플래그 : 1
(2) 시프트 >> C->A->Q : 1 0011 1101 : 0 1001 1110
M 레지스터 : 1101
Q 레지스터 : 1110
A 레지스터 : 1001
C 플래그 : 0
-------------------------------------------------------------
t(3) >> bit : 0검사
-> 0이므로 시프트 연산만 수행
(1) 시프트 >> C->A->Q : 0 1001 1110 : 0 0100 1111
M 레지스터 : 1101
Q 레지스터 : 1111
A 레지스터 : 0100
C 플래그 : 0
-------------------------------------------------------------
t(4) >> bit : 1검사
-> 1이므로 덧셈 + 시프트 연산 수행
(1) 덧셈 A + M -> A : 0100 + 1101 = 0001 (carry 1 발생)
M 레지스터 : 1101
Q 레지스터 : 1111
A 레지스터 : 0001
C 플래그 : 1
(2) 시프트 >> C->A->Q : 1 0001 1111 : 0 1000 1111
M 레지스터 : 1101
Q 레지스터 : 1111
A 레지스터 : 1000
C 플래그 : 0
-------------------------------------------------------------
Q 레지스터의 모든 bit 검사 완료
>> 최종 결과 : 1000 1111 = 128 + 8 + 4 + 2 + 1 = 143
2의 보수 곱셈
- Booth 알고리즘 사용
- M 레지스터, 병렬 가산기 사이에 보수기를 추가
- Q 레지스터 우측에 Q`이라고 부르는 1-bit 레지스터를 추가
- Q 레지스터의 각각의 bit, Q`값을 함께 제어 회로로 입력
- Q 레지스터가 우측 시프트 될 때, Q 레지스터의 가장 우측 bit가 Q` 레지스터에 저장
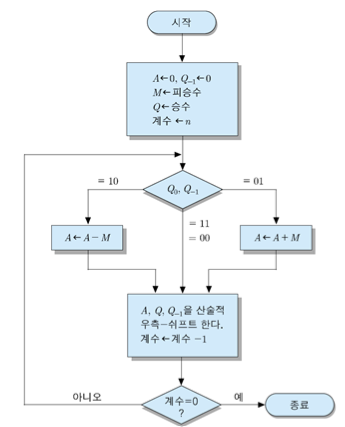
- M 레지스터 : 피승수 저장
- Q 레지스터 : 승수 저장
- A 레지스터, Q`bit : 초기에 전부 0으로 초기화
- 계수 N
- 승수의 bit수를 저장 >> 각 승수 bit에 대한 연산이 종료되면 N - 1 -> N >> N이 0이되면 연산 종료
1. Q 레지스터의 최하위 bit, Q`의 bit를 함께 제어회로에 입력
2. 두 bit가 같은지 다른지 검사
- 동일 : 산술적 우측 시프트
- 10 : A - M -> A >> 산술적 우측 시프트
- 01 : A + M -> A >> 산술적 우측 시프트
## 1101 X 1011 (-3 X -5) ##
>> 피승수 = 1101
>> 승수 = 1011
>> Q`에는 산술적 우측 시프트 연산 시, Q 레지스터의 최하위 bit 저장
----------------------------------------------------------------
t(0) >> 초기상태
M 레지스터 : 1101
Q 레지스터 : 1011
A 레지스터 : 0000
Q` : 0
N : 4
----------------------------------------------------------------
이제 Q 레지스터(승수)의 최하위 bit, Q`를 비교해서 검사
----------------------------------------------------------------
t(1) >> Q 레지스터의 최하위 bit = 1, Q` = 0
-> 10이므로, A - M -> A 연산 후 산술적 우측 시프트 수행
(1) A - M -> A : 0000 - 1101 = 0000 + 0011 = 0011
M 레지스터 : 1101
Q 레지스터 : 1011
A 레지스터 : 0011
Q` : 0
N : 4
(2) 산술적 우측 시프트 >> A->Q->Q` : 0011 1011 0 : 0 001 1101 1
M 레지스터 : 1101
Q 레지스터 : 1101
A 레지스터 : 0001
Q` : 1
N : 3
----------------------------------------------------------------
t(2) >> Q 레지스터의 최하위 bit = 1, Q` = 1
-> 11이므로(동일) 산술적 우측 시프트 연산만 수행
(1) 산술적 우측 시프트 >> A->Q->Q` : 0001 1101 1 : 0 000 1110 1
M 레지스터 : 1101
Q 레지스터 : 1110
A 레지스터 : 0000
Q` : 1
N : 2
----------------------------------------------------------------
t(3) >> Q 레지스터의 최하위 bit = 0, Q` = 1
-> 01이므로 A + M -> A 연산 후 산술적 우측 시프트 수행
(1) A + M -> A : 0000 + 1101 = 1101
M 레지스터 : 1101
Q 레지스터 : 1110
A 레지스터 : 1101
Q` : 1
N : 2
(2) 산술적 우측 시프트 >> A->Q->Q` : 1101 1110 1 : 1 110 1111 0
M 레지스터 : 1101
Q 레지스터 : 1111
A 레지스터 : 1110
Q` : 0
N : 1
----------------------------------------------------------------
t(4) >> Q 레지스터의 최하위 bit = 1, Q` = 0
-> 10이므로 A - M -> A 연산 후 산술적 우측 시프트 수행
(1) A - M -> A : 1110 - 1101 = 1110 + 0011 = 0001
M 레지스터 : 1101
Q 레지스터 : 1111
A 레지스터 : 0001
Q` : 0
N : 1
(2) 산술적 우측 시프트 >> A->Q->Q` : 0001 1111 0 : 0 000 1111 1
M 레지스터 : 1101
Q 레지스터 : 1111
A 레지스터 : 0000
Q` : 1
N : 0
----------------------------------------------------------------
Q 레지스터의 모든 bit 검사 완료
>> 최종 결과 : 0000 1111 = 15
나눗셈
- A ÷ B = q .... r
- A = 피제수 / B = 제수 / q = 몫 / r = 나머지
부호 없는 정수 나눗셈
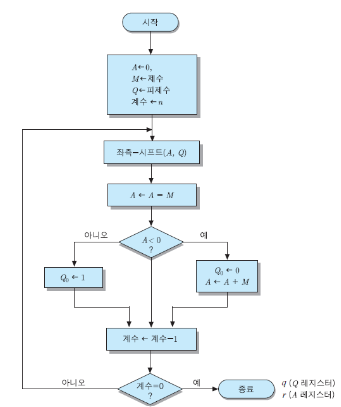
- A 레지스터
- 0으로 초기화
- Q 레지스터
- 피제수 저장
- M 레지스터
- 제수 저장
- 계수 N
- 피제수의 bit수를 저장
- 각 피제수 bit에 대한 연산이 종료되면 N - 1 -> N
- N이 0이되면 연산 종료
1. A 레지스터, Q 레지스터를 논리적 좌측-시프트
- (A 레지스터와 Q 레지스터 간에 직렬 Data 전송 :: 실제로는 서로 이어져있다)
2. A - M -> A
- A의 값이 음수 : Q 레지스터의 최하위 bit를 0으로 설정 >> A + M -> A
- A의 값이 양수 : Q 레지스터의 최하위 bit를 1로 설정
## 10010011 ÷ 1011 (147 ÷ 11) ##
>> 피제수 = 10010011
>> 제수 = 1011
>> Q 레지스터 : 피제수 저장
>> M 레지스터 : 제수 저장
>> A 레지스터 : 처음에는 0으로 초기화
>> 계수 N : 피제수의 bit수만큼 저장
>> 최종적으로 Q 레지스터 값 = 몫, A 레지스터 값 = 나머지
----------------------------------------------------------------------------------------
t(0) >> 초기상태
A 레지스터 : 0000 0000
Q 레지스터 : 1001 0011
M 레지스터 : 0000 1011
N : 8
----------------------------------------------------------------------------------------
t(1)
(1) 좌측 시프트 >> A<-Q : 0000 0000 1001 0011 : 0000 0001 0010 0110
A 레지스터 : 0000 0001
Q 레지스터 : 0010 0110
M 레지스터 : 0000 1011
N : 8
(2) A - M -> A : 0000 0001 - 0000 1011 = 0000 0001 + 1111 0101 = 1111 0110 = -10 (음수)
-> Q의 최하위 bit를 0으로 설정 / A + M -> A : 1111 0110 + 0000 1011 = 0000 0001
A 레지스터 : 0000 0001
Q 레지스터 : 0010 0110
M 레지스터 : 0000 1011
N : 7
----------------------------------------------------------------------------------------
t(2)
(1) 좌측 시프트 >> A<-Q : 0000 0001 0010 0110 : 0000 0010 0100 1100
A 레지스터 : 0000 0010
Q 레지스터 : 0100 1100
M 레지스터 : 0000 1011
N : 7
(2) A - M -> A : 0000 0010 - 0000 1011 = 0000 0010 + 1111 0101 = 1111 0111 = -9 (음수)
-> Q의 최하위 bit를 0으로 설정 / A + M -> A : 1111 0111 + 0000 1011 = 0000 0010
A 레지스터 : 0000 0010
Q 레지스터 : 0100 1100
M 레지스터 : 0000 1011
N : 6
----------------------------------------------------------------------------------------
t(3)
(1) 좌측 시프트 >> A<-Q : 0000 0010 0100 1100 : 0000 0100 1001 1000
A 레지스터 : 0000 0100
Q 레지스터 : 1001 1000
M 레지스터 : 0000 1011
N : 6
(2) A - M -> A : 0000 0100 - 0000 1011 = 0000 0100 + 1111 0101 = 1111 1001 = -7 (음수)
-> Q의 최하위 bit를 0으로 설정 / A + M -> A : 1111 1001 + 0000 1011 = 0000 0100
A 레지스터 : 0000 0100
Q 레지스터 : 1001 1000
M 레지스터 : 0000 1011
N : 5
----------------------------------------------------------------------------------------
t(4)
(1) 좌측 시프트 >> A<-Q : 0000 0100 1001 1000 : 0000 1001 0011 0000
A 레지스터 : 0000 1001
Q 레지스터 : 0011 0000
M 레지스터 : 0000 1011
N : 5
(2) A - M -> A : 0000 1001 - 0000 1011 = 0000 1001 + 1111 0101 = 1111 1110 = -2 (음수)
-> Q의 최하위 bit를 0으로 설정 / A + M -> A : 1111 1110 + 0000 1011 = 0000 1001
A 레지스터 : 0000 1001
Q 레지스터 : 0011 0000
M 레지스터 : 0000 1011
N : 4
----------------------------------------------------------------------------------------
t(5)
(1) 좌측 시프트 >> A<-Q : 0000 1001 0011 0000 : 0001 0010 0110 0000
A 레지스터 : 0001 0010
Q 레지스터 : 0110 0000
M 레지스터 : 0000 1011
N : 4
(2) A - M -> A : 0001 0010 - 0000 1011 = 0001 0010 + 1111 0101 = 0000 0111 = 7 (양수)
-> Q의 최하위 bit를 1로 설정
A 레지스터 : 0000 0111
Q 레지스터 : 0110 0001
M 레지스터 : 0000 1011
N : 3
----------------------------------------------------------------------------------------
t(6)
(1) 좌측 시프트 >> A<-Q : 0000 0111 0110 0001 : 0000 1110 1100 0010
A 레지스터 : 0000 1110
Q 레지스터 : 1100 0010
M 레지스터 : 0000 1011
N : 3
(2) A - M -> A : 0000 1110 - 0000 1011 = 0000 1110 + 1111 0101 = 0000 0011 = 3 (양수)
-> Q의 최하위 bit를 1로 설정
A 레지스터 : 0000 0011
Q 레지스터 : 1100 0011
M 레지스터 : 0000 1011
N : 2
----------------------------------------------------------------------------------------
t(7)
(1) 좌측 시프트 >> A<-Q : 0000 0011 1100 0011 : 0000 0111 1000 0110
A 레지스터 : 0000 0111
Q 레지스터 : 1000 0110
M 레지스터 : 0000 1011
N : 2
(2) A - M -> A : 0000 0111 - 0000 1011 = 0000 0111 + 1111 0101 = 1111 1100 = -4 (음수)
-> Q의 최하위 bit를 0으로 설정 / A + M -> A : 1111 1100 + 0000 1011 = 0000 0111
A 레지스터 : 0000 0111
Q 레지스터 : 1000 0110
M 레지스터 : 0000 1011
N : 1
----------------------------------------------------------------------------------------
t(8)
(1) 좌측 시프트 >> A<-Q : 0000 0111 1000 0110 : 0000 1111 0000 1100
A 레지스터 : 0000 1111
Q 레지스터 : 0000 1100
M 레지스터 : 0000 1011
N : 1
(2) A - M -> A : 0000 1111 - 0000 1011 = 0000 1111 + 1111 0101 = 0000 0100 = 4 (양수)
-> Q의 최하위 bit를 1로 설정
A 레지스터 : 0000 0100
Q 레지스터 : 0000 1101
M 레지스터 : 0000 1011
N : 0
----------------------------------------------------------------------------------------
N = 0이므로 연산 종료
최종 결과
- 몫 = Q 레지스터 값 = 13
- 나머지 = A 레지스터 값 = 4
결과확인
>> 147 ÷ 11 = 11 X 13 + 4
>> 잘 나누어진걸 확인할 수 있다
2의 보수 나눗셈
- A 레지스터
- 초기에 0 저장
- Q 레지스터
- 피제수 저장
- M 레지스터
- 제수 저장
- 계수 N
- 피제수의 bit수를 저장
- 각 피제수 bit에 대한 연산이 종료되면 N - 1 -> N
- N이 0이되면 연산 종료
1. A 레지스터, Q 레지스터를 논리적 좌측-시프트
- (A 레지스터와 Q 레지스터 간에 직렬 Data 전송 :: 실제로는 서로 이어져있다)
- A 레지스터, M 레지스터 부호 비트 동일 : A - M -> A
- A 레지스터, M 레지스터 부호 비트 다름 : A + M -> A
2-1. A의 부호가 연산 전과 동일
- Q 레지스터의 최하위 bit를 1로 설정
2-2. A의 부호가 연산 전과 다름
- Q 레지스터의 최하위 bit를 0으로 설정
- A를 연산 전의 값으로 복구
3-1. Q 레지스터, M 레지스터 부호 동일
- 몫 = Q 레지스터 값
3-2. Q 레지스터, M 레지스터 부호 다름
- 몫 = Q 레지스터 값의 2의 보수
4. 나머지 = A 레지스터 값
## 01101101 ÷ 11111011 (109 ÷ -5) ##
>> 피제수 = 01101101
>> 제수 = 11111011
>> A 레지스터 : 초기에 0 저장
>> Q 레지스터 : 피제수 저장
>> M 레지스터 : 제수 저장
>> 계수 N : 피제수의 bit수만큼 저장
----------------------------------------------------------------------------------------
t(0) >> 초기상태
A 레지스터 : 0000 0000
Q 레지스터 : 0110 1101
M 레지스터 : 1111 1011
N : 8
----------------------------------------------------------------------------------------
t(1)
(1) 좌측 시프트 >> A<-Q : 0000 0000 0110 1101 : 0000 0000 1101 1010
A 레지스터 : 0000 0000
Q 레지스터 : 1101 1010
M 레지스터 : 1111 1011
N : 8
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
>> A + M -> A : 0000 0000 + 1111 1011 = 1111 1011
(3) 연산 전, 후의 A 부호비트가 서로 다르다
-> Q 레지스터의 최하위 bit를 0으로 설정 / A 레지스터를 연산 전으로 복구
A 레지스터 : 0000 0000
Q 레지스터 : 1101 1010
M 레지스터 : 1111 1011
N : 7
----------------------------------------------------------------------------------------
t(2)
(1) 좌측 시프트 >> A<-Q : 0000 0000 1101 1010 : 0000 0001 1011 0100
A 레지스터 : 0000 0001
Q 레지스터 : 1011 0100
M 레지스터 : 1111 1011
N : 7
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
>> A + M -> A : 0000 0001 + 1111 1011 = 1111 1100
(3) 연산 전, 후의 A 부호비트가 서로 다르다
-> Q 레지스터의 최하위 bit를 0으로 설정 / A 레지스터를 연산 전으로 복구
A 레지스터 : 0000 0001
Q 레지스터 : 1011 0100
M 레지스터 : 1111 1011
N : 6
----------------------------------------------------------------------------------------
t(3)
(1) 좌측 시프트 >> A<-Q : 0000 0001 1011 0100 : 0000 0011 0110 1000
A 레지스터 : 0000 0011
Q 레지스터 : 0110 1000
M 레지스터 : 1111 1011
N : 6
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
>> A + M -> A : 0000 0011 + 1111 1011 = 1111 1110
(3) 연산 전, 후의 A 부호비트가 서로 다르다
-> Q 레지스터의 최하위 bit를 0으로 설정 / A 레지스터를 연산 전으로 복구
A 레지스터 : 0000 0011
Q 레지스터 : 0110 1000
M 레지스터 : 1111 1011
N : 5
----------------------------------------------------------------------------------------
t(4)
(1) 좌측 시프트 >> A<-Q : 0000 0011 0110 1000 : 0000 0110 1101 0000
A 레지스터 : 0000 0110
Q 레지스터 : 1101 0000
M 레지스터 : 1111 1011
N : 5
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
>> A + M -> A : 0000 0110 + 1111 1011 = 0000 0001
(3) 연산 전, 후의 A 부호비트가 서로 동일하다
-> Q 레지스터의 최하위 bit를 1로 설정
A 레지스터 : 0000 0001
Q 레지스터 : 1101 0001
M 레지스터 : 1111 1011
N : 4
----------------------------------------------------------------------------------------
t(5)
(1) 좌측 시프트 >> A<-Q : 0000 0001 1101 0001 : 0000 0011 1010 0010
A 레지스터 : 0000 0011
Q 레지스터 : 1010 0010
M 레지스터 : 1111 1011
N : 4
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
>> A + M -> A : 0000 0011 + 1111 1011 = 1111 1110
(3) 연산 전, 후의 A 부호비트가 서로 다르다
-> Q 레지스터의 최하위 bit를 0으로 설정 / A 레지스터를 연산 전으로 복구
A 레지스터 : 0000 0011
Q 레지스터 : 1010 0010
M 레지스터 : 1111 1011
N : 3
----------------------------------------------------------------------------------------
t(6)
(1) 좌측 시프트 >> A<-Q : 0000 0011 1010 0010 : 0000 0111 0100 0100
A 레지스터 : 0000 0111
Q 레지스터 : 0100 0100
M 레지스터 : 1111 1011
N : 3
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
>> A + M -> A : 0000 0111 + 1111 1011 = 0000 0010
(3) 연산 전, 후의 A 부호비트가 서로 동일하다
-> Q 레지스터의 최하위 bit를 1로 설정
A 레지스터 : 0000 0010
Q 레지스터 : 0100 0101
M 레지스터 : 1111 1011
N : 2
----------------------------------------------------------------------------------------
t(7)
(1) 좌측 시프트 >> A<-Q : 0000 0010 0100 0101 : 0000 0100 1000 1010
A 레지스터 : 0000 0100
Q 레지스터 : 1000 1010
M 레지스터 : 1111 1011
N : 2
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
>> A + M -> A : 0000 0100 + 1111 1011 = 1111 1111
(3) 연산 전, 후의 A 부호비트가 서로 다르다
-> Q 레지스터의 최하위 bit를 0으로 설정 / A 레지스터를 연산 전으로 복구
A 레지스터 : 0000 0100
Q 레지스터 : 1000 1010
M 레지스터 : 1111 1011
N : 1
----------------------------------------------------------------------------------------
t(8)
(1) 좌측 시프트 >> A<-Q : 0000 0100 1000 1010 : 0000 1001 0001 0100
A 레지스터 : 0000 1001
Q 레지스터 : 0001 0100
M 레지스터 : 1111 1011
N : 1
(2) A 레지스터와 M 레지스터의 부호비트가 다르다
-> A + M -> A : 0000 1001 + 1111 1011 = 0000 0100
(3) 연산 전, 후의 A 부호비트가 서로 동일하다
-> Q 레지스터의 최하위 bit를 1로 설정
A 레지스터 : 0000 0100
Q 레지스터 : 0001 0101
M 레지스터 : 1111 1011
N : 0
----------------------------------------------------------------------------------------
N = 0이므로 연산 종료
최종 결과
- 몫 = Q 레지스터와 M 레지스터의 부호비트가 다르다
>> 몫 = Q 레지스터의 값에 대한 2의 보수
>> 0001 0101 -> 1110 1011 = -128 + (64 + 32 + 8 + 2 + 1) = -21
- 나머지 = A 레지스터 값 = 4
결과확인
>> (109 ÷ -5) = (-5)X(-21) + 4
>> 잘 나누어진걸 확인할 수 있다부동소수점 수 표현
- 매우 큰 수, 매우 작은 수를 표현할 수 있다
- 10진 소수점의 위치를 적절히 이동
- 소수점의 위치는 지수(exponent)를 이용해서 표시
N = (-1)SM×BE
- M : 가수(mantassa)
- B : 기수(base)
- E : 지수(exponent)
ex) 2.74×1014
- M : 2.74
- B : 10
- E : +14
>> 2진 부동소수점 수는 B=2이다
표현 범위
▶ 양수
- 0.5 × 2-128 ~ (1-2-24) × 2127
▶ 음수
- -(1-2-24) × 2127 ~ -0.5 × 2-128

2진 부동소수점 수
- 사용하는 bit 수에 따라 32-bit/64-bit형식으로 표현
- 32-bit : 단일-정밀도
- 64-bit : 복수-정밀도
32-bit 부동소수점 형식

- 지수 필드 bit 수 증가
- 표현 가능한 수의 범위 확장
- 가수 필드 bit 수 증가
- 정밀도(precision) 증가
정규화된 표현
- 하나의 수에 대해서 여러 개의 표현을 방지하는 표현
- ± 0.1bbb.....b×2E
- 소수점 바로 우측 bit는 무조건 '1'이 되도록 위치를 조정
- 소수점 아래 첫번째 비트는 무조건 1이기 때문에 가수필드에 저장할 필요가 없다
- 소수점 아래 24자리 수까지 표현이 가능하다
>> 첫번째 비트를 제외한 나머지 비트들만 작성하면 된다
▶ Example) 0.1101 × 25
- 부호(S) 비트 : 0
- 지수(E) 필드 : 0000 0101
- 가수(M) 필드 : 101 0000 0000 0000 0000 0000
| S | 지수(E) 필드 | 가수(M) 필드 |
| 0 | 0000 0101 | 101 0000 0000 0000 0000 0000 |
- 정수 0에 대한 표현이 문제
- 가수(M) = 0
- 지수(E) = 어떠한 값이 들어와도 상관없다 - (문제점)
- 이러한 문제점 해결 : 지수를 바이어스된 수(Biased Number)로 표현
- 지수 bit에 바이어스값을 더해준 값을 지수 필드로 사용
- 0-검사를 용이하게 하기 위해서 사용한다
▶ Example) N = -13.625 >> 32-bit 부동소수점 표현 (바이어스 = 128)
13.62510 = 1101.1012 = 0.1101101 × 24
- 부호(S) 비트 = 1
- 지수(E) 필드 = 4 + 128 = 0000 0100 + 1000 0000 = 1000 0100
- 가수(M) 필드 = 101101 0000 0000 0000 0000 0
| S | 지수(E) 필드 | 가수(M) 필드 |
| 1 | 1000 0100 | 101101 0000 0000 0000 0000 0 |
IEEE 754 표준 부동소수점 수의 형식
N = (-1)S(1.M)×2E
- 32-bit 단일-정밀도 부동소수점 수의 표현
- 가수(M) 필드 : 부호화-크기 표현 사용
- 지수(E) 필드 : 바이어스 127 사용
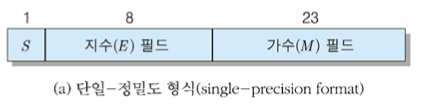

N = (-1)S(1.M)×2E
- 64-bit 복수-정밀도 부동소수점 수의 표현
- 가수(M) 필드 : 부호화-크기 표현 사용
- 지수(E) 필드 : 바이어스 1023 사용


4배수-정밀도 부동소수점 수의 표현 (IEEE 754-2008)

- 128-bit 4배수-정밀도 부동소수점 수의 표현
- 가수(M) 필드 : 부호화-크기 표현 사용
- 지수(E) 필드 : 바이어스 16383 사용
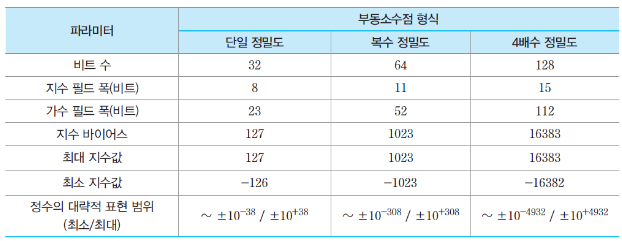
부동소수점 수 산술 연산
덧셈 / 뺄셈
- 두 수의 소수점 위치를 일치 (지수 조정)
- 가수들 간에 덧셈/뺄셈 수행
- 정규화
곱셈
- 가수들 곱하기
- 지수들 더하기
- 정규화
나눗셈
- 가수들 나누기
- 피제수의 지수 - 제수의 지수
- 계산된 지수에 바이어스 값 더하기
- 정규화
