[Data Structure] 계수 정렬 - Counting Sort

계수 정렬 (Counting Sort)

Stable sort 

• 비교하지 않는 정렬 알고리즘
• 좁은 범위의 Data를 정렬할 때 효과적
• 입력받는 수의 범위가 한정되어 있을 때 사용

 

총 배열 3개가 필요 (정렬할 배열 A, 누적 합 배열 C, 최종 정렬된 배열 result)

- 추가 배열 C

• 배열 A에 존재하는 각 요소들의 등장횟수를 오름차순으로 저장하고, 배열 C의 맨 앞 인덱스부터 차례대로 값들을 누적해서 저장
• 배열 C는 결국 배열 A의 각 요소들의 인덱스를 저장

 

시간복잡도

- O(n + k) → k = 배열의 최댓값

 

장점

- O(n)의 매우 빠른 속도로 정렬 가능

 

단점

- 음수/실수는 정렬 못함

- 추가적인 메모리 공간이 필요하고 값의 분포에 따라 메모리 낭비가 심해질 수 있다

 

과정

1. 정렬할 배열 A, 배열 A의 요소에 대한 누적 합 배열 C, 최종 정렬완료 배열 result 생성
2. 배열 A의 각 요소들의 등장횟수를 오름차순으로 배열 C에 저장
3. 배열 C에 저장된 각 요소들의 등장횟수를 앞에서부터 차례대로 누적해서 더한 값들로 업데이트
4. 배열 A의 끝에서부터 역순으로 순회하면서, 각 요소의 인덱스를 배열 C로부터 확인해서 배열 result의 해당 인덱스에 저장
5. 저장하면 배열 C의 해당 인덱스는 -1을 해준다

 

 

※ Example

과정 1 ~ 3

배열 A

→ {5, 5, 3 ,4, 5, 1, 0, 4, 1, 3, 0, 2, 4, 2, 3, 0}

배열 C

A의 각 요소	0	1	2	3	4	5
등장 횟수	3	2	2	3	3	3

↓

배열 C (앞에서부터 누적)

A의 각 요소	0	1	2	3	4	5
인덱스	3	5	7	10	13	16

 

과정 4 ~ 5

배열 A : {5, 5, 3 ,4, 5, 1, 0, 4, 1, 3, 0, 2, 4, 2, 3, 0}

→ 배열 C에서 요소 0의 인덱스 = 3

→ result배열의 인덱스3에 0 저장

→ 배열 C에서 요소 0의 인덱스 -1

result index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
			0

A의 각 요소	0	1	2	3	4	5
인덱스	2	5	7	10	13	16

 

배열 A : {5, 5, 3 ,4, 5, 1, 0, 4, 1, 3, 0, 2, 4, 2, 3, 0}

→ 배열 C에서 요소 3의 인덱스 = 10

→ result배열의 인덱스10에 3 저장

→ 배열 C에서 요소 3의 인덱스 -1

result index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
			0							3

A의 각 요소	0	1	2	3	4	5
인덱스	2	5	7	9	13	16

 

배열 A : {5, 5, 3 ,4, 5, 1, 0, 4, 1, 3, 0, 2, 4, 2, 3, 0}

→ 배열 C에서 요소 2의 인덱스 = 7

→ result배열의 인덱스7에 2 저장

→ 배열 C에서 요소 2의 인덱스 -1

result index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
			0				2			3

A의 각 요소	0	1	2	3	4	5
인덱스	2	5	6	9	13	16

 

배열 A : {5, 5, 3 ,4, 5, 1, 0, 4, 1, 3, 0, 2, 4, 2, 3, 0}

→ 배열 C에서 요소 4의 인덱스 = 13

→ result배열의 인덱스13에 4 저장

→ 배열 C에서 요소 4의 인덱스 -1

result index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
			0				2			3			4

A의 각 요소	0	1	2	3	4	5
인덱스	2	5	6	9	12	16

 

배열 A : {5, 5, 3 ,4, 5, 1, 0, 4, 1, 3, 0, 2, 4, 2, 3, 0}

→ 배열 C에서 요소 2의 인덱스 = 6

→ result배열의 인덱스6에 2 저장

→ 배열 C에서 요소 2의 인덱스 -1

result index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
			0			2	2			3			4

A의 각 요소	0	1	2	3	4	5
인덱스	2	5	5	9	12	16

---

배열 A : {5, 5, 3 ,4, 5, 1, 0, 4, 1, 3, 0, 2, 4, 2, 3, 0}

→ 배열 C에서 요소 5의 인덱스 = 14

→ result배열의 인덱스14에 5 저장

→ 배열 C에서 요소 5의 인덱스 -1

result index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
	0	0	0	1	1	2	2	3	3	3	4	4	4	5	5	5

A의 각 요소	0	1	2	3	4	5
인덱스	0	3	5	7	10	13

 

 

Counting_Sort Code

static void counting_sort(int [] A, int[] C, int [] result){
        for(int i=0; i<A.length; i++)
            C[A[i]]++; // A의 각 요소 등장횟수를 C의 해당 인덱스 저장

        for(int i=1; i<C.length; i++){
            C[i] += C[i-1]; // C 앞에서부터 차례대로 누적 합 저장 accumulate
        }

        for(int i=A.length-1; i>=0; i--){
            int value = A[i]; // 배열 A의 마지막 요소 확인
            C[value]--; // 해당 요소의 인덱스 -1
            result[C[value]] = value; 
            // 해당 요소를 result 인덱스(배열 C에서의 해당 요소 인덱스)에 저장
        }
    }

 

 

Full Code

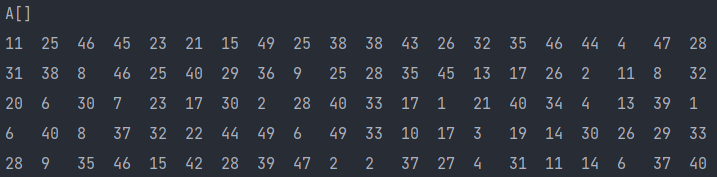
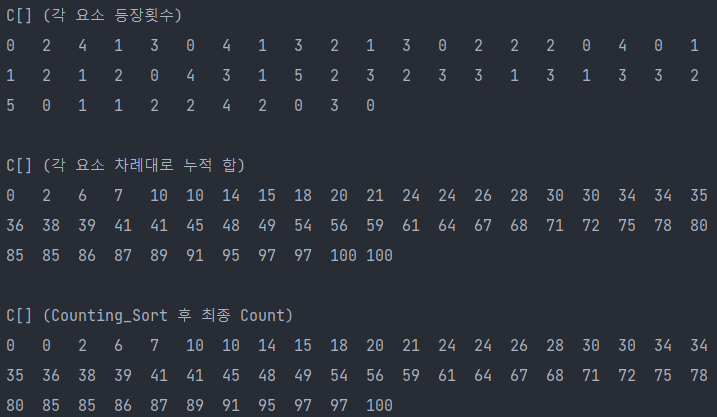
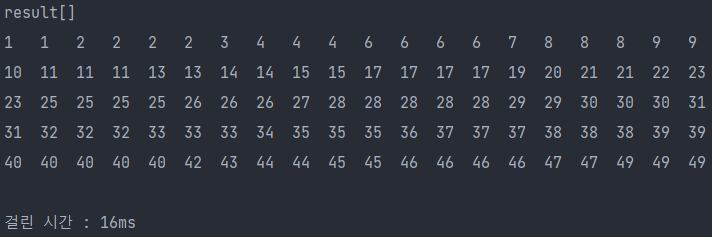
package Sort;

import java.util.Calendar;

public class Counting_Sort_1 {
    public static void main(String[] args){
        int [] A = new int[100]; // 정렬할 배열 A
        int [] C = new int[51]; // A의 요소들에 대한 등장횟수, 차례대로 누적 합
        int [] result = new int[100]; // A의 최종 정렬 배열 저장

        for(int i=0; i<A.length; i++)
            A[i] = (int)(Math.random()*51); // 0~50

        // 정렬 전 A 출력
        System.out.print("A[]");
        for(int i=0; i<A.length; i++){
            if(i%20==0) System.out.println();
            System.out.print(A[i] + "\t");
        }
        System.out.println("\n");

        counting_sort(A, C, result);
    }
    static void counting_sort(int [] A, int[] C, int [] result){
        Calendar before = Calendar.getInstance();
        for(int i=0; i<A.length; i++)
            C[A[i]]++; // A의 각 요소 등장횟수를 C의 해당 인덱스 저장
        System.out.print("C[] (각 요소 등장횟수)");
        for(int i=0; i<C.length; i++){
            if(i%20==0) System.out.println();
            System.out.print(C[i] + "\t");
        }
        System.out.println("\n");

        for(int i=1; i<C.length; i++){
            C[i] += C[i-1]; // C 앞에서부터 차례대로 누적 합 저장 accumulate
        }
        System.out.print("C[] (각 요소 차례대로 누적 합)");
        for(int i=0; i<C.length; i++){
            if(i%20==0) System.out.println();
            System.out.print(C[i] + "\t");
        }
        System.out.println("\n");

        for(int i=A.length-1; i>=0; i--){
            int value = A[i]; // 배열 A의 마지막 요소 확인
            C[value]--; // 해당 요소의 인덱스 -1
            result[C[value]] = value;
            // 해당 요소를 result 인덱스(배열 C에서의 해당 요소 인덱스)에 저장
        }
        Calendar after = Calendar.getInstance();
        // A의 각 요소 count 저장한 배열 C 출력
        System.out.print("C[] (Counting_Sort 후 최종 Count)");
        for(int i=0; i<C.length; i++){
            if(i%20==0) System.out.println();
            System.out.print(C[i] + "\t");
        }
        System.out.println("\n");

        // 정렬 후 최종 result 배열 출력
        System.out.print("result[]");
        for(int i=0; i<result.length; i++){
            if(i%20==0) System.out.println();
            System.out.print(result[i] + "\t");
        }
        System.out.println("\n");

        int time = after.get(Calendar.MILLISECOND) - before.get(Calendar.MILLISECOND);
        System.out.println("걸린 시간 : " + time + "ms");
    }
}