2022. 5. 28. 16:16ㆍMajor`/인공지능
모수 모델 : Parametric Model
모수 모델이란 "인간"이 가설 함수의 범위(다항식 차수)를 Agent에게 알려주고, 차수를 바탕으로 Agent는 Learning을 통해서 Parameter를 구하는 방식이다
- A Learning Model summarizing data with a set of parameteres of fixed size

비-모수 모델 : Nonparametric Model
비-모수 모델은 인간이 학습하라고 부여한 학습데이터를 "학습"에 사용하지 않고 전부 보유만 하고 있다
- 학습을 안하고 놀고있고, 받은 훈련 데이터는 가지고 있기만 한다
매번 input이 들어올때마다 "보유하고 있는 학습 데이터를 사용"해서 해당 input에 대한 결과를 도출해내는 방식이다
- 개체-기반 학습(Instance-Based Learning)이라고 한다
따라서 비-모수 모델은 학습 데이터를 통해서 만들어낸 "가설함수"를 test할 때 사용하는게 아니라, 아예 학습 데이터 그 자체를 매 순간 test할 때 사용하겠다는 것이다
그러므로 "가설함수"를 얻으려는 노력조차 하지 않는다
분류 (모수 vs 비-모수)
모수 선형 분류

부여받은 훈련 데이터에 대해서 "학습"을 진행함에 따라 "가설함수 : 선형 모델"을 구하였다
이후에 들어오는 input에 대해서는 그냥 가설함수에 적용만 시키면 그에 따른 output이 도출된다
비모수 분류 (k-NN)
k-Nearest-Neighbors (k-NN) Classification이란 보유한 학습 데이터중에 input에 가장 근접한 k개의 학습 데이터들을 활용해서 input을 Classification하는 방법이다

k가 너무 작을 경우(k=1) 가장 가까운 1개의 "보유 훈련 데이터"에 의존해서 Classification되기 때문에 주어진 훈련 데이터에 대한 Overfitting 문제가 발생할 수 있다
비-모수 모델에서는 {새로운 input - 보유한 훈련 데이터들}간의 "비교"가 필수적이다
- 모수 모델은 학습을 통해서 얻은 가설함수에 의해서 input이 결정되기 때문에 굉장히 빠르다
- 반면 비모수 모델은 k개에 대한 "모든 거리"를 계산해서 결정해야 하기 때문에 시간이 굉장히 오래 걸린다
근데 이런 비모수 모델은 학습을 안하고 놀고 있기 때문에 그 시간이 아깝다고 생각이 든다
따라서 학습을 안하는 시간에는 "보유한 학습 데이터들을 군집화"시키면 된다
- 보유한 학습데이터 끼리끼리 그룹 만들어주기
※ 유사도 검사
비-모수 모델에서 {input - 학습 데이터들}간의 "유사도 (= 거리)"계산은 반드시 필요한 부분이다
그런데 만약에 input이 "수치값"이 아니라 Object이면 어떻게 비교할까??
거리 척도 1) Minkowski Distance


거리 척도 2) Hamming Distance
Hamming Distance란 두 String간 서로 다른 부분이 몇개인지 check하는 것이다

거리 척도 3) Normalization (정규화)

회귀 (모수 vs 비-모수)
모수 선형 회귀

1차원 입력 x1에 대해서 Agent는 학습을 통해서 가설함수를 찾아냈다

비-모수 회귀
Regression은 input이 1차원이기 때문에 input에 대한 NN에 의존해서 카테고리화 할 수 없다
- input간의 유사도가 output간의 유사도는 아니기 때문
※ Connect Dots

input : 0.8
0.8과 가장 가까운 훈련 데이터는 (0, 1) & (1, 3)이다
따라서 이 2개의 훈련 데이터를 사용하자
(0, 1) & (1, 3)을 이은 직선에다가 "0.8"을 적용시켜주면 input(0.8)에 대한 Regression이 된다
※ k-nearest neighbors Average

input : 0.8
3-nearest이니까 input(0.8)에 대해서 가장 가까운 훈련 데이터들은 (0, 1) & (1, 3) & (2, 2.6)이다
따라서 {0, 1, 2}에 대한 {1, 3, 2.4}의 average를 구해서 해당 average를 input에 대한 output으로 정해주면 된다
- input(0.8) >> output : (1 + 3 + 2.6) / 3 = 2.2
※ k-nearest neighbors Linear Regression

이거는 input의 가장 가까운 훈련데이터들에 대해서 "선형 모델"을 만들고 그 선형 모델을 기준으로 input을 Regression하면 된다
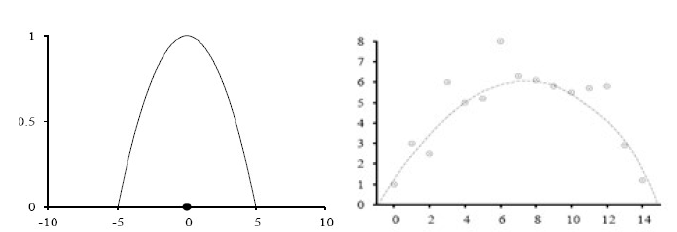
※ Locally Weighted Regression (with a quadratic kernel of width k = 10)

k-NN은 결국 새로운 input에 대해서 "보유한 훈련 데이터 중에서 k개를 사용"해서 input에 대한 output을 도출해내는 방식이다
하지만 Locally는 일단 주어진 훈련 데이터 "모두" 사용해서 output을 도출하는 방식이다
- input에 가까운 학습 데이터일수록 "가중치"를 더 많이 부여해서 나의 output에 영향을 더 많이 주게 된다
"보유한 훈련 데이터" & "새로운 input"간에 유사도를 측정해서 원래 데이터를 나의 예측 데이터에 얼만큼 반영할까? 를 결정한다
>> 유사도는 거리로 측정하면 간편하다 : 나(input)와 가까운 훈련 데이터일수록 내가 많이 반영한다
▶ Kernel Function
커널 함수는 "거리 반비례 함수"라고 생각하면 된다 :: K(Distance(x(j), x(q))
- Kernel Function자체를 "Weight"로 활용하자

x(j)는 원래 알고있는 데이터이고, x(q)는 새롭게 예측(input)할 데이터이다
식을 보면 알수있듯이 거리가 멀수록 해당 훈련 데이터의 반영 비율을 낮춘다