[AI] 인공 신경망

[AI] 인공 신경망

2022. 5. 28. 15:47ㆍMajor`/인공지능

Neural Network

Neural Networks는 신경세포(Neuron)들의 "연결(Link)"로 구현되어 있다

Neuron들을 "Unit"이라고 부르기도 한다

Input Links는 N차원으로 구성이 되고, 각 Input Link마다 "가중치"가 존재한다

{Input Value & Weight}를 각 input마다 곱해서 들어온 총 합(Input Function)이 "Neuron으로 들어오는 Input Value"라고 할 수 있다

이렇게 Neuron내부로 들어온 Value는 "Neuron의 Activation Function"에 의해서 Processing되고, Processing이 완료된 값이 Output으로 나가게 된다

Input Function

Input Function이란 들어오는 value마다 각각의 weight를 곱하고 이를 전부 더하는 함수이다

Activation Functioin

Input Function에 의해서 들어온 Neuron's Value는 "Activation Function"을 최종적으로 거쳐서 Output으로 나가게 된다

Activation Function에는 크게 2가지 종류가 있다

(1) Hard Threshold

Neuron의 활성화 함수로 Hard Threshold를 적용한다는 의미이다

Perceptron

(2) Logistic/Sigmoid Function

Neuron의 활성함수로 Logistic/Sigmoid Function을 적용한다는 의미이다

Neural Network Structure

네트워크 구조는 크게 2가지로 분류할 수 있다

1) Feed Forward Network

신호(Link)를 앞으로 계속 전달하는 네트워크 구조이다

그리고 하나의 Neuron은 "다음 Layer의 모든 Neuron"에게 신호를 전달한다 (Fully Connected FFN)

2) Recurrent Network

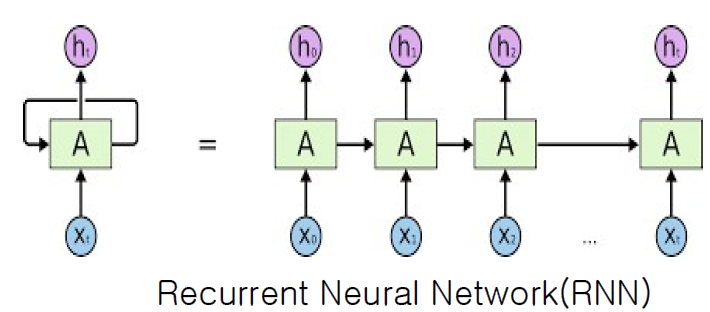
Output이 다시 Input으로 되돌아올 수 있는 네트워크 구조이다

Feed-Forward Networks (순방향 신경망)

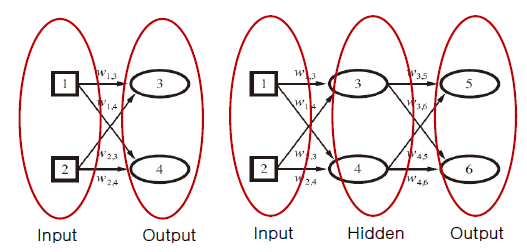
크게 {Input Layer / Output Layer}로 나눌 수 있고 이 가운데에 "Hidden Layer"가 N개 존재할 수 있다

Hidden Layer이 없는 {Input Layer + Output Layer} : Single Layer FFN
{Input Layer + (Hidden Layer) + Output Layer} : Multi Layer FFN

Input/Output은 외부에서도 보이고 반드시 존재해야 하는 Layer이지만, Hidden Layer는 외부에서 보이지 않고 반드시 있을 필요는 없는 Layer이다

(1) Single-Layer Feed-Forward NNs

좌측 표는 "학습 데이터"이고 이에 맞는 신경망이 우측에 존재한다

(x1, x2)가 input이고 (y1, y2)가 output이다.

2차원 입력에 대해서 2차원 출력이 도출되는 것을 파악할 수 있다

결국 "Learning"을 통해서 알아내는 것은 각 Link의 "가중치"이다

가중치를 알아내는 것이 "신경망 학습"이다

가중치를 어떻게 주냐에 따라서 신경망이 "AND" 연산 과정을 도출해낼 수 있고, "OR" 연산 과정을 도출해낼 수 있고, "XOR" 연산 과정을 도출해낼 수 있다

여기서 저 신경망 구조를 자세히 살펴보자

input은 (x1, x2)가 연속으로 들어오지만, 그에 대한 output인 (y1, y2)는 서로 연관이 없다

따라서 (x1, x2)에 대해서 y1을 구하고, (x1, x2)에 대해서 y2를 구하는 작업을 따로 수행할 수 있다

Multi Layer의 경우 중간에 Hidden Layer가 존재하기 때문에 output간에 연관이 존재한다

※ 학습 규칙 (= 가중치 Update하는 규칙)

만약 활성화 함수로 Threshold가 적용된 Neuron이라면 "퍼셉트론 학습 규칙"을 통해서 가중치를 갱신한다

반면에 활성화 함수로 Logistic Function이 적용된 Neuron이라면 "체인 학습 규칙"을 통해서 가중치를 갱신한다

※ Single Layer 문제점

Single Layer는 위에서 {AND, OR}같은 선형으로 분류하는 것은 편리하게 수행할 수 있다

하지만 XOR같이 선형으로 분류할 수 없는 비선형 모델의 경우 Neuron하나로는 불가능하다

>> Single Layer 여러개를 겹쳐서 만든 Multi Layer을 통해서 비선형 분류/회귀를 하자

(2) Multilayer Feed-Forward NNs

결국 Single Layer의 경우 선형/초평면에 대해서는 "선형 분류/회귀"가 가능하다

하지만 샘플들이 선형으로 나뉘어지지 않는 경우는 Multi Layer를 활용해서 비선형 분류/회귀를 수행해야 한다

Hidden Layer가 많아지면 많아질수록 비선형 경계를 더 정확히 찾을 수 있지만, Link수가 더 많아짐에 따라 학습에 의해 알아내야 할 가중치가 더 많아진다

※ Example)

각 Unit의 활성화 함수로 ReLU를 적용했다고 하자

ReLU : max{0, output}

보면 어느 한 Unit에서는 다음 Layer의 모든 Unit에게 Link가 나가고 있다

최종적 Output Layer를 보게되면

Frame 8 : {1, 2, 3, 4, 5, 6, 7}에 의해 영향을 받음
Frame 9 : {1, 2, 3, 4, 5, 6, 7}에 의해 영향을 받음

따라서 동일한 Layer의 각각의 Unit들은 이전 모든 Unit으로부터 영향을 받는 것을 알 수 있다

input layer & weight에 의한 각 Layer의 Unit들의 value를 계산해보자

Unit (Neuron)	Input Function	Activation Function
Frame 3	1×1 + 2×(-4) = -7	0
Frame 4	1×8 + 2×(-7) = -6	0
Frame 5	1×(-10) + 2×9 = 8	8
Frame {3, 4, 5}는 다음 Layer인 Frame {6, 7}에 영향을 미친다
Frame 6	0×(-0.2) + 0×(0.3) + 8×(-0.1) = -0.8	0
Frame 7	0×3 + 0×1 + 8×(0.1) = 0.8	0.8
Frame {6, 7}은 다음 Layer(output)인 Frame {8, 9}에 영향을 미친다
Frame 8	0×8 + 0.8×10 = 8	8
Frame 9	0×5 + 0.8×3 = 2.4	2.4

역전파 알고리즘 (Back Propagation)

학습 데이터로 주어지는 것은 {input / output}이지 Hidden Layer Value까지 주어지는 것은 아니다.

하지만 학습은 신경망 내부에 존재하는 "모든 Neuron"에 대해서 이루어져야 한다

여기서 우리가 부여받은 학습 데이터는 {input / output}인데 어떻게 Hidden Neuron까지 학습시킬지가 문제가 된다

따라서 Multi Layer에서의 학습 문제는 "Hidden Neuron을 어떻게 학습시킬건가"에 달려있다

1. 초기 모든 link들에 대한 가중치는 random하게 주어진다
2. 각 Neuron(Unit)들은 input에 대해서 {입력 함수 - 활성화 함수}를 적용해서 output을 도출해낸다
3. 활성함수로 Sigmoid (Logistic Function)을 적용한다
>> 물론 다른 활성화 함수를 사용해도 문제는 없다

일단 처음에는 random으로 설정된 weight에 의해서 output이 도출된다

>> 당연히 실제 값과 신경망에 의한 예측값 사이에는 오차가 존재할 것이다

여기서 이 오차들에 대해서 "손실함수"를 적용해서 실제 Error Rate가 어느정도인지 알아봐야 한다

결국 "Learning"의 목적은 Error Rate를 최소화하는 것이다

여기서 "역전파 알고리즘"이란 Sequence Result에 대한 Error Rate를 "output -> input"방향으로 역-전파 하면서 가중치를 다시 갱신하는 알고리즘이다

중간중간에 구한 오차값을 "역으로 전파"해서 모두에게 알린다는 의미로 "역전파 알고리즘"이 되었다

역으로 전파할때는 해당 Link의 weight를 다시 곱해서 전파해준다

for training_repeat
  for training_sets

		// 가중치로 net, out 계산 
		forward pass              

		//output 레이어에서 시작해 input + 1 레이어로
		for i = output layer -> i = input layer + 1     
			for all nodes in layer i
				set delta
			
			//layer i와 i-1 사이에 있는 가중치 갱신
		  	for all weights between layer i and layer i-1  
				update weight

처음에는 각 Link에 random한 값을 설정해주고 1번 Simulate해서 발생한 오차를 "K"라고 하자

▶ Example) Neuron 6

Neuron(6)은 Output Layer {5, 6}중 하나이다

그리고 6은 {3, 4}의 값들을 각 Link의 가중치에 곱한 것을 합친 value를 가지고 있다

여기서 "오류 역-전파"를 수행해보자

6은 {3, 4}로부터 값을 얻었기 때문에 {3, 4}둘에게 오차 K를 분배해서 전파해줘야 한다

여기서 분배는 다시 각 Link의 가중치에 비례해서 부여해준다

<Neuron 3이 책임져야 할 오차>
5가 책임지는 오차에 대해서 w(3, 5)에 비례한 오차 + 6이 책임지는 오차에 대해서 w(3, 6)에 비례한 오차

<Neuron 4가 책임져야 할 오차>
5가 책임지는 오차에 대해서 w(4, 5)에 비례한 오차 + 6이 책임지는 오차에 대해서 w(4, 6)에 비례한 오차

이런 과정을 통해서 오류가 역-전파가 되고, 그에 따라서 각 Link의 가중치는 다음과 같이 전부 update된다

저작자표시 변경금지

Coding -> 블로그 이전

Coding