2022. 4. 23. 15:42ㆍMajor`/인공지능
CSP (제약 만족 문제)
대학교 시간표를 짤때도 여러 강의를 자신의 시간표로 넣을 때 각 강의간에 제약조건에 존재한다.
이러한 과정을 통해서 시간표를 완성했다면 우리는 "시간표 짜기"라는 문제에 대한 제약 조건을 만족했다고 할 수 있다
"인공지능"의 많은 문제들은 제약 조건을 만족시켜가면서 해결하는데 이러한 문제의 Goal State는 "주어진 제약 조건을 만족"시킨 상태이다.
CSP의 3가지 요소
1) Variable
문제에서 제약 조건을 만족시켜줘야 하는 "변수들"
- 각 변수들 사이에는 제약조건이 존재하고, 제약조건을 만족하도록 각 변수에 Domain 값을 설정해줘야 한다
2) Domain
변수에 할당되는 "값들의 집합"
- 제약조건을 만족할 수 있도록 변수들에 Domain 값을 잘 설정해줘야 한다
3) Constraint
변수들 간에 존재하는 제약조건
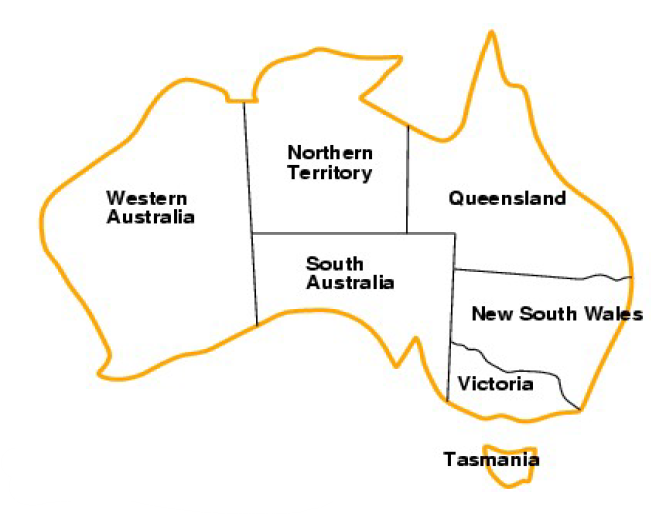
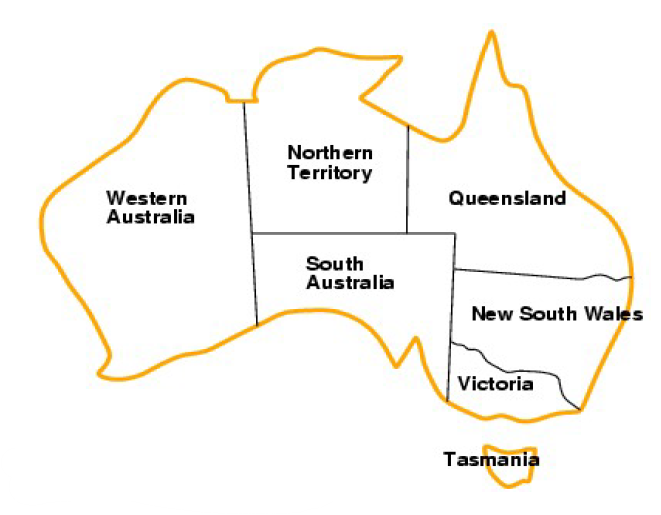
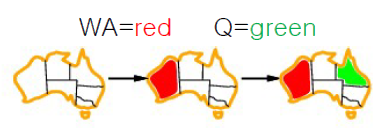
Example 1) Map Coloring

우리는 이러한 Map에 색깔을 칠하려고 한다
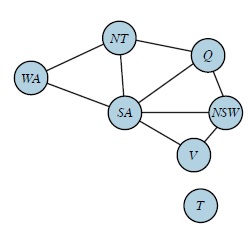
매번 Map을 그리기는 귀찮기 때문에 이러한 Map을 "Constraint Graph"로 변경할 수 있다

"Constraint Graph"에서는 "제약조건이 존재하는 Variable들 간에는 Arc(Edge)로 연결"
단, C-G에서는 제약조건의 상세 내용은 기재할 수 없다
Variables : {WA, NT, SA, Q, NSW, V, T}
Domains : {RED, BLUE, GREEN}
Constraints : "인접 지역은 반드시 다른 색깔로 칠하기"

위 그림은 제약조건을 만족해서 각 Variable들에게 Domain Value를 설정해준 것이다
>> Solutions are complete and consistent assignments
Complete란 "모든 Variable은 특정 Domain Value를 가져야 한다"라는 것이다
Consistent란 "모든 제약 조건을 만족"해야 한다는 것이다
Example 2) Cryptarithmetic

이러한 암호수식이 존재하고 우리가 알아내야 할 것은 "각 알파벳별로 어떤 숫자가 들어가야 저 식을 만족하냐" 이다
Variables : {T, W, O, F, U, R, X1, X2, X3}
>> 여기서 X1, X2, X3는 각 자리수별로 carry되는 숫자를 나타낸 것이다
Domains : {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Constrains : {T, W, O, F, U, R}은 전부 다른 숫자로 구성되어야 한다 -- (1)
▶ O + O = R + 10 × X1-- (2)
▶ X1 + W + W = U + 10 × X2 -- (3)
▶ X2 + T + T = O + 10 × X3 -- (4)
▶ X3 = F (T ≠ 0 & F ≠ 0) -- (5)

X1, X2, X3의 예를 들으면 위의 사진처럼 설정이 된다
어차피 각 자릿수의 최대값은 9 + 9 = 18이므로 X1, X2, X3는 최대값이 1이다
따라서 X1, X2, X3는 {0, 1} 중 하나의 값이 될 것이다
>> 이제 Cryptarithmetic을 Constraint Graph로 표현해보자

이 경우는 2개의 변수쌍 간에만 제약조건이 존재하는게 아니라 "여러 변수들 사이에 제약 조건이 존재"하는 고차제약의 경우라서 Constraint Graph가 꽤 복잡하다
Variables 분류
1) 이산 변수 : Discrete Variables
▶ 유한 집합 (Finite Domains)
n개의 Variable과 사이즈가 d인 Domain → Complete Assignments를 하기 위한 시간 복잡도 : O(dn)
▶ 무한 집합 (Infinite Domains)
Integers / Strings / ... 과 같은 집합들
- Job Scheduling / ...
따라서 무한 집합의 경우 "Constraint Language"가 필요하다 → StartJob(1) + 5 ≤ StartJob(3)
2) 연속 변수 : Continuous Variables
Constrains 분류
1) 단항 제약
단일 변수에 대한 Domain 제약
→ SA ≠ "green"
2) 이항 제약
두 변수에 대한 서로간의 제약
→ SA ≠ WA
3) 고차 제약
여러 변수들(3개 이상의 변수) 간에 서로 제약
→ X1 + W + W = U + 10 × X2
이러한 CSP를 해결하기 위한 가장 대중적인 방법은 "Backtracking Search"이다
Initial State : 초기 상태를 {} (빈 공간)으로 정해주기
Successor Function : 정해지지 않은 변수에 대해서 Domain 하나를 할당
>> 여기서 정해준 Domain Value는 "반드시 이전에 정해준 Variable의 Domain Value와 충돌하면 안된다"
>> "제약 위반 X"를 보장
Goal Test : 현재 Assignment가 "Complete"한지 확인한다
>> 만약 만족을 하지 못한다면 Backtracking
탐색 결과(Solution)은 Variable에 Domain Value를 설정해주는 순서와는 상관 없지만, 이 순서는 "탐색 종료 시간"과는 연관이 있다

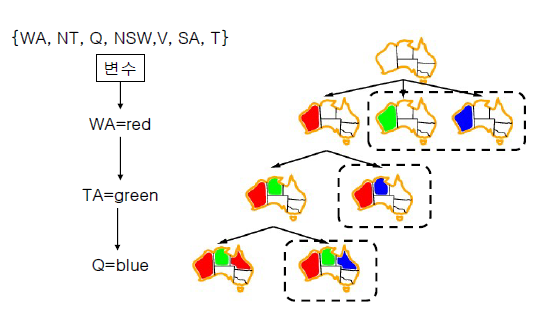
이러한 과정으로 Backtracing Search가 진행된다
하지만 무작정 Backtracking Search를 하게 되면 "탐색의 효율성"이 별로일 것이다
따라서 우리는 Backtracking Search의 효율성 향상을 위한 몇가지 방식이 존재한다
Backtracing Search의 효율성 향상
원래 Backtracking Search는 모든 node를 다 뒤지기 때문에 "Variable & Domain"의 Size가 커질수록 탐색의 효율성은 떨어지게 된다
>> General-Purpose Heuristics 사용
1) 어떤 변수부터 먼저 Domain 할당??
Variable Ordering Heuristic (변수 순서 휴리스틱)
Most Constrained Variable
"제약을 가장 많이 받는 변수부터 정해주자"
- 결국 해당 변수는 본인이 택할 수 있는 Domain Value의 범위가 가장 적을 것이다 :: Minimum Remaining Values
>> 결국 "색의 제약" = "Domain 범위"가 가장 작은 Variable을 선택하자
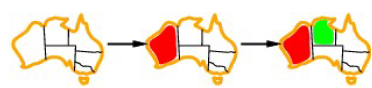
이 상태에서 "각 Variable별 Domain 범위"를 생각해보자
- WA : 이미 칠해짐 (red)
- NT : 이미 칠해짐 (green)
- SA : WA(red), NT(green), Q, NSW, V → "Only Blue"
- Q : NT(green), SA, NSW → "Red or Blue"
- NSW : Q, SA, V → "Red or Green or Blue"
- V : SA, NSW → "Red or Green or Blue"
- T : 0 → "Red or Green or Blue"
Domain 범위가 가장 작은 지역은 "Only Blue"인 SA이다
따라서 SA를 먼저 Domain Value를 할당해줘야 한다

이 상태에서 "변수 별로 제약 받는 횟수"를 생각해보자
이거는 "초기 상태"이므로 모든 Variable이 Domain 범위가 동일하므로 "Most Constrained Variable"로 선택할 수 없다
>> 동률(Tie)이 나올 경우 "Most Constraining Variable"으로 내려가서 선택(Tie-Breaker)을 해줘야 한다
Most Constraining Variable
"다른 Variable에게 제약을 가장 많이 주는 변수부터 정해주자"

이 상태에서 "변수 별로 남에게 제약을 주는 횟수"를 생각해보자
- WA : NT, SA = 2
- NT : WA, SA, Q = 3
- SA : WA, NT, Q, NSW, V = 5
- Q : NT, SA, NSW = 3
- NSW : Q, SA, V = 3
- V : NSW, SA = 2
- T : 0
SA가 남에게 가장 많이 제약을 주기 때문에 SA부터 Domain Value를 할당해줘야 한다
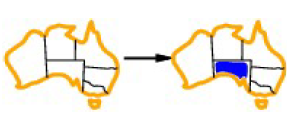
- WA : NT = 1
- NT : WA, Q = 2
- Q : NT, NSW = 2
- NSW : Q, V = 2
- V : NSW = 1
- T : 0
이 경우 제약을 남에게 많이 주는 Variable이 {NT, Q, NSW}로 동률이 되었다
>> "Most Constraining Variable"에서도 Tie가 나올 경우 이 때는 Tie Variables 중에서 그냥 Random으로 선택해준다
변수를 정해주는 것은 일단 "Most Constrained Variable"을 기본으로 하고, 여기서 Tie가 발생할 경우 "Most Constraining Variable"을 통해서 정해주는 것이다
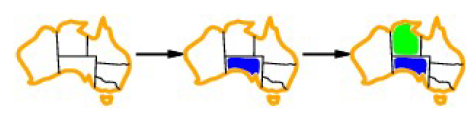
- WA : NT(green), SA(blue) → "Only Red"
- NT : 이미 정해짐 (green)
- SA : 이미 정해짐 (blue)
- Q : NT(green), SA(blue), NSW → "Only Red"
- NSW : Q, SA(blue), V → "Red or Green"
- V : NSW, SA(blue) → "Red or Green"
- T : "Red or Green or Blue"
여기서 {WA, Q}가 Tie이므로 "Most Constrainig Variable"을 통해서 정해주어야 한다
- WA : 0
- Q : NSW = 1
Q가 남에게 더 제약을 많이 주므로 "Q"를 선택한다

이러한 과정으로 계속 진행해주면 된다
2) 정해진 변수에게 어떤 Domain Value를 먼저 배정??
Value Selection Heuristic (값 선택 휴리스틱)
- 이것은 1) 과정을 먼저 수행하고 고려해야 하는 Heuristic이다
Least Constraining Value
해당 변수에게 "다른 변수들에게 제약을 가장 적게 주는 값"을 배정해주자
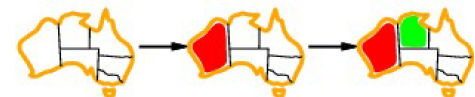
1)에서 Q를 선택해주었고 이제 2)에서 Q에게 어떤 값을 배정해줄까를 고민해야 한다
이 때 Q의 Domain 범위는 {"Red", "Blue"}이다
- WA : 이미 정해짐 (red)
- NT : 이미 정해짐 (green)
- SA : WA(red), NT(green), Q, NSW, V → "Only Blue"
- Q : NT(green), SA, NSW → "Red or Blue"
- NSW : Q, SA, V → "Red or Green or Blue"
- V : NSW, SA → "Red or Green or Blue"
- T : "Red or Green or Blue"
▶ Q에게 "Red" 배정
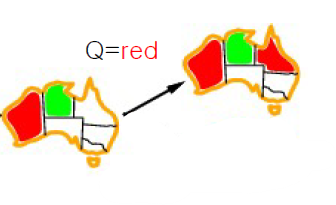
여기서 다른 변수들의 Domain 범위를 생각해보자
- WA : 이미 정해짐 (red)
- NT : 이미 정해짐 (green)
- SA : WA(red), NT(green), Q(임시 red), NSW, V → "Only Blue"
- 여전히 Blue는 가능하다
- Q : 임시 "Red"
- NSW : Q(임시 red), SA, V → "Green or Blue"
- {Red, Green, Blue}에서 {Green, Blue}로 범위가 좁혀졌다
- V : NSW, SA → "Red or Green or Blue"
- T : "Red or Green or Blue"
▶ Q에게 "Blue" 배정
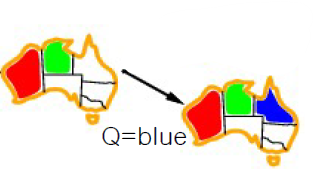
여기서 다른 변수들의 Domain 범위를 생각해보자
- WA : 이미 정해짐 (red)
- NT : 이미 정해짐 (green)
- SA : WA(red), NT(green), Q(blue), NSW, V → X
- 원래 {Blue}였지만 Q에 Blue를 칠함으로써 "SA에는 이제 칠할 수 있는 색깔이 없다"
- Q : 임시 "Blue"
- NSW : Q(임시 blue), SA, V → "Red or Green"
- {Red, Green, Blue}에서 {Red, Green}으로 범위가 좁혀졌다
- V : NSW, SA → "Red or Green or Blue"
- T : "Red or Green or Blue"
>> "Red" Case, "Blue" Case를 각각 봤을 때 Q에 Blue를 칠하는 순간 SA에는 더이상 경우의 수가 존재하지 않는다. 따라서 "Q에는 Red를 배정"
3) 해당 Sequence의 실패 가능성을 파악하는 방법
Forward Checking (전향 검사)
"한계까지 도달해서 파악"
1) Domain이 배정되는 않은 Variable들에 대해서 "Domain 범위"를 매번 Check
2) 만약 "Domain 범위"에 아무것도 없는 Variable을 발견할 시 즉시 Backtracking
>> 어느 한 Variable의 "Domain 범위"에 아무것도 없을 때까지 일단 탐색 진행

초기 각 Variable들에 대한 Domain 범위는 위와 같다
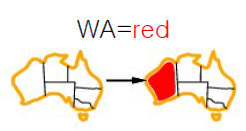
WA에 Red를 칠했을 경우 나머지 Variable들에 대한 Domain 범위를 Update해야 한다

이 다음으로 Q에는 Green & V에는 Blue를 칠했다고 가정하자
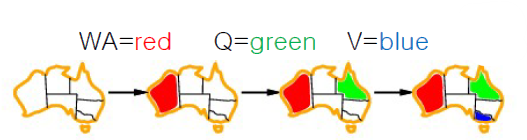
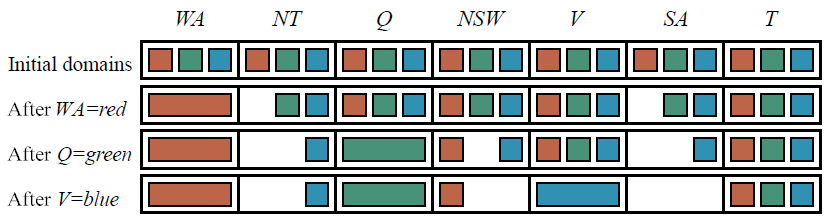
여기서 SA의 Domain 범위를 보게되면 아무것도 없다
따라서 "Backtracking"해줘야 한다
여기서 V에게 Blue말고 {Red, Green}중 어떤 값을 줘야할지 다시 고민해야 한다
Constraint Propagation (제약 전파)
"한계에 도달하기 전에 미리 파악"
물론 Forward Checking도 좋은 방식이지만 결국 어느 한 Variable의 Domain 범위에 아무것도 없을때까지 탐색을 진행하게 된다
Constraint Propagation은 Domain 범위가 없을때까지 탐색하는게 아니라 :: Domain이 존재하는 가운데 미리 "실패 가능성"을 탐지하는 방식이다
>> 지역적으로 제약조건에 대한 탐지를 강화하는 방식이다
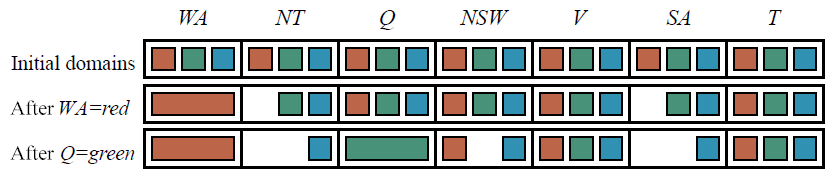
여기서 Forward Checking은 V에게 Blue를 할당해주고 SA의 Domain에 아무것도 없는 것을 확인하고 Backtracking한다
하지만 Constraint Propagation은 이전단계에서 "실패 가능성"을 감지할 수 있다
Constraint Propagation에서는 "Arc Consistency"를 통해서 "실패 가능성"을 탐지한다
X → Y의 Arc가 존재한다고 하자
이러면 X의 현재 Domain 범위에 대해서, Y는 그에 대응되는 Domain 값이 적어도 하나는 존재해야 한다
예를 들어서 X(red, blue) & Y(blue)라면 red → blue는 대응되지만 X의 blue에 대해서는 Y는 어떠한 값도 대응되지 못한다
여기서 "실패 가능성"을 탐지하고 Backtracking을 한다
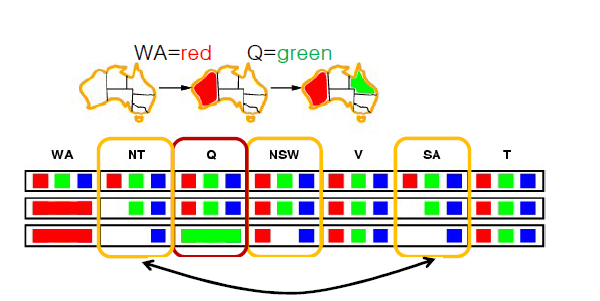
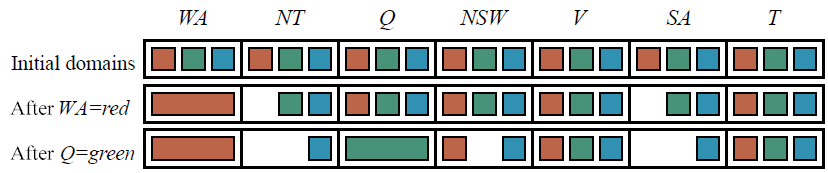
Q에 Green을 배정했을 경우 Domain 범위가 변경되는 Variable은 {NT, NSW, SA}이다
저 3개의 Variable간에 "Arc Consistency"를 확인해보자
▶ NT - NSW
NT(Blue) → NSW(Red, Blue)
여기서는 NT의 blue에 대한 NSW의 대응 값 Red가 존재한다
NT(Blue) ← NSW(Red, Blue)
하지만 여기서 NSW(blue)에 대해서 NT에는 어떠한 값도 대응되지 못한다
따라서 "실패 가능성"을 탐지했으므로 Backtracking해서 Q의 값을 다시 설정해줘야 한다(Green 제외)
물론 Constraint Propagation은 계산량은 굉장히 많아지지만, 그에 따라서 탐색의 효율성도 굉장히 좋아진다
지금까지의 CSP 탐색 기술들은 전부 Global Search를 기준으로 설명을 하였다
하지만 CSP 탐색 기술에 Local Search를 적용할 수도 있다
Local Search for CSP
Global Search(Backtracking)은 매 순간 하나의 Variable에 Domain Value를 할당한다
Local Search의 관점에서 바라보면
▶ Initial State
Global Search와는 다르게 "아예 초기에 모든 Variable에 Domain Value를 할당"
▶ Evaluation Function
초기에 전부 할당을 하고, "평가 함수"에 의해서 각 Variable의 Domain Value를 재할당한다
여기서 우리는 "재할당할 변수 선택" & "선택된 변수에 어떤 값으로 재할당해줄까"를 고민해야 한다
- 재할당 변수 선택 : Randomly Select Any Conflicted Variable
- 어떤 값으로 재할당 : Min-Conflicts Heuristic
선택할 때는 "충돌 발생시킨 Variable들 중 아무거나 하나"를 선택한다
재할당은 "재할당할 경우 충돌을 가장 적게 유발하는 값"을 선택한다
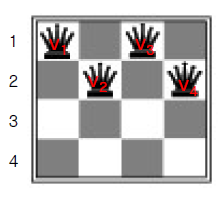
4-Queens에서의 Local Search CSP를 적용해보자
먼저 초기상태에서는 모든 Variable에 Domain Value를 할당하였다
{V1 = 1, V2 = 2, V3 = 1, V4 = 2}
여기서 평가함수를 적용한 값(충돌 횟수)는 "-5"가 된다
이제 1) 재할당 할 변수 선택 & 2) 재할당 값을 정해주어야 한다
1) 재할당 변수 선택
충돌을 일으키는 변수는 {V1, V2, V3, V4}가 있고 여기서 random으로 V4를 선택했다고 하자
2) 재할당 값 선택
현재 V4에는 (2)가 할당되어 있으므로 (2)를 제외한 (1, 3, 4) 중 하나를 선택해야 한다
만약 V4에 1을 재할당했을 경우 → "-5"
만약 V4에 3을 재할당했을 경우 → "-3"
만약 V4에 4을 재할당했을 경우 → "-5"
따라서 충돌을 가장 적게 유발시키는 Domain(3)으로 V4를 재할당 해줘야 한다
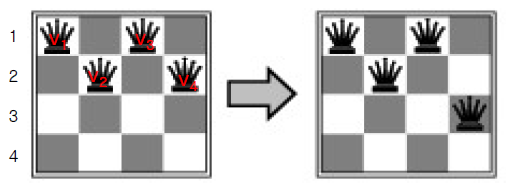
{V1 = 1, V2 = 2, V3 = 1, V4 = 3}
이런 식으로 Local Search에서의 CSP를 적용하면 된다
