[AI] Local Search

[AI] Local Search

2022. 4. 12. 21:58ㆍMajor`/인공지능

Local Search Algorithms

많은 "최적화 문제"에서는 Goal까지의 경로가 중요한게 아니라 Goal에 도달하는 그 자체가 중요하다
상태 공간 탐색의 경우 초기 상태 & 목표 상태가 주어지고 Action들의 Sequence에 의해서 Goal에 도달한다
지역 탐색의 경우 초기 상태만 주어지고 목표 상태는 모르는 상태에서 오직 현재 상태보다 더 나은 상태로 가려는 탐색 방식이다

그에 따른 제약조건이 굉장히 많지만 지역 탐색은 제약조건을 최대한 많이 만족할 수 있는 Goal을 찾는 것이 목표이다

>> 목표 상태까지의 Path는 관심 X / 오로지 목표 상태에 도달하는 그자체가 중요하다

특징

1) "상태 공간"이란 해당 공간안에 존재하는 state들이 모두 그들만의 value를 보유하고 있다

- "상태 평가 함수"로 각 state를 평가함으로써 각 state는 value를 가지게 된다

2) 항상 "하나의 Current State"만을 유지한다

- 항상 current state를 향상시키려고 노력한다
- 향상되지 않으면 탐색은 종료된다

Hill-Climbing & Simulated Annealing에 적용되는 특징이다
Local Beam & GA는 여러개의 current state를 유지한다

3) 초기 상태는 항상 random하게 주어진다

- 주어진 초기 상태에서 neighbor들을 평가한 후 current state보다 더 나은 neighbor중에 best를 골라서 향한다
- 선택되지 않은 나머지 후보들은 영원히 버려진다

4) 언제나 목표는 "Global Maximum"

- Hill-Climbing Local Search Algorithm의 경우는 "Local Maximum"문제가 발생할 수 있다. 이를 해결하기 위한 다른 Local Search Algorithm들이 존재한다

N-Queens

초기 상태가 이렇게 주어졌다
Local Search에서는 각 state마다 value가 존재한다 했었고 state별로 value는 각 column별로 어느 index에 있냐가 value이다

v1 = 1
v2 = 2
v3 = 1
v4 = 2

이 때 "Queens간의 충돌 쌍을 찾아보자"

(v1, v2) (v1, v3) (v2, v3) (v2, v4) (v3, v4)

총 5개의 충돌 쌍이 존재한다
>> 따라서 초기 상태의 "상태 평가 함수" f는 "-5"의 value를 갖게 된다

그리고 v4를 index(3)으로 옮겼다

N-Queens에서는 state 변경을 "하나의 state 변경"으로 간주한다

그리고 변경된 state의 "상태 평가 함수" f는 "-3"의 value를 갖게 된다

>> 이전의 state보다 더 나아진 state가 되었다

그리고 또 이렇게 v2를 옮겼다
이 때 변경된 state의 "상태 평가 함수" f는 "-1"의 value를 갖게 된다

이렇게 Local Search는 매 순간 이전 state보다 나아지려는 탐색 특성을 가지고 있다

1) Hill-Climbing Search

말 그대로 "언덕 오르기 탐색"이다. 여기서 "언덕을 내려가는 것"은 간주하지 않는다

이 특성 때문에 "Local Maximum" 문제가 발생한다

초기 상태는 Local Search에서 항상 random이므로 S(0)가 초기 상태라고 가정하자
Local Search의 특성 중 하나인 "더 나은 state로 가기"를 따르면 S(0)에서는 neighbor state인 S(2)가 상태 평가 value로 보았을 때 current state보다 낫다
따라서 S(0)에서 S(2)로 "상태 변경"을 한다

그리고 나서 S(2)에서 neighbot들을 바라보니 전부 S(2)보다 value가 낮다
따라서 Hill-Climbing Search에서는 S(2)에서 탐색이 종료된다

그러나 전체적으로 봤을 때 S(6)가 Global Maximum이라는 사실을 알 수 있지만 "Local Search"는 Global하게 탐색을 하지 않고 Local하게 탐색을 진행하기 때문에 "Local 범위"내에서 더 나은 state가 없으면 탐색이 종료된다

>> 이러한 문제를 "Local Maximum" 문제라고 한다

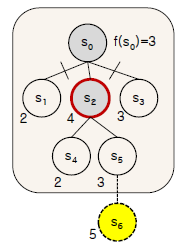
위의 탐색과정을 Tree로 펼쳐보면 위의 사진과 같다
Local Search의 또 다른 특징은 "선택되지 못한 neighbor state들은 영원히 고려사항에서 제외된다"이다
상태 공간 탐색의 경우 이번에 선택을 하지 않았어도 해당 node들은 다음 선택의 후보군으로 남아있게 된다
하지만 지역 탐색의 경우에는 이번에 선택되지 않으면 영원히 선택되지 않는다

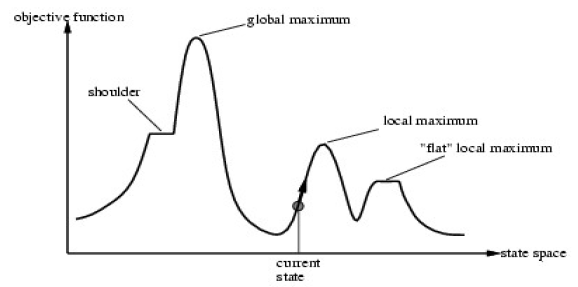
초기 상태가 random으로 주어지기 때문에 초기 상태에 따라서 당연히 Global Maximum으로 도달할 수 있을 수도 있고 없을 수도 있다
따라서 이러한 Local Maximum 문제를 해결하기 위한 여러가지 Local Search Algorithm이 존재한다

2) Simulated Annealing Search

Annealing이란 "담금질"의 개념이다
대장장이가 금속을 "열에 가열했다가 냉각했다가"를 반복하면서 원하는 형태의 물질을 생성해낸다

Hill-Climbing의 경우에 빗대어서 보면 Hill-Climbing은 열을 가열하기만 하는 탐색 전략이다
하지만 Simulated Annealing은 열을 가열 + 냉각하면서 탐색을 진행한다

일단 금속에 열을 처음 가하게 된다면 처음에는 모양이 쉽게쉽게 변형이 되겠지만 시간이 지남에 따라 금속은 점차 굳게 되면서 모양이 쉽게 변하지 않는다

S-A도 물론 초기 상태는 random하게 주어진다
하지만 S-A에는 온도/시간(T/t)라는 개념이 존재한다

"그리고 H-C에는 항상 best move만 허용하지만, S-A는 가끔 bad move도 허용한다"

>> bad move를 통해서 "Local Maximum"문제를 해결할 가능성이 존재한다

위의 Pseudo Code를 보게 되면

"current"의 초기 상태는 문제로부터 random하게 생성이 된다
T = 0 : 온도가 0이 된다면 시간이 지남에 따라 냉각이 완료되었기 때문에 current state를 return해준다
next state는 "current state의 neighbor중에 random으로 선택된 하나"이다
그리고 (next - current)를 통해서 "value의 변화"를 계산한다

value > 0 : next가 더 좋은 state이고 Local Search 전략에 들어맞기 때문에 당연히 next로 이동한다
value < 0 : 이 때 물론 next로 가게 된다면 "bad move"이겠지만 "특정 확률"에 의해 next로 가도록 해준다

value < 0이므로 e^-1은 1/e가 된다

→ next가 current보다 훨씬 value가 안좋을수록 next로 갈 확률은 적어진다

→ T가 작아질수록 : 온도가 내려갈수록 : 냉각이 될수록 next로 갈 확률은 적어진다

→ 온도가 내려간다는 것은 시간이 지난다는 것을 의미하고 따라서 시간이 흐를수록 next로 갈 확률은 적어진다

H-C와 S-A의 차이를 Pseudo Code에서 설명하자면
H-C는 절대로 "value < 0"을 고려하지 않는다 >> "Local Maximum" 발생
S-A는 "value < 0"도 특정 확률에 의해 고려한다 >> "Local Maximum" 해결 가능성 존재

하지만 S-A가 "Local Maximum" 문제를 완전히 해결했다고 볼 수는 없다

3) Local Beam Search

H-C나 S-A는 current state가 "오직 하나"만 존재한다
하지만 Local Beam Search는 current state가 여러 개 존재한다

>> 따라서 각 current state를 병렬적으로 탐색함에 따라서 다양한 경로를 동시에 탐색할 수 있다

먼저 초기 state는 "K"개의 random하게 생성된 state가 주어진다
매 탐색마다 K개의 current state는 유지된다
각 current state별로 탐색을 진행하다가 어느 하나의 state라도 Goal이라면 즉시 탐색은 종료된다

하지만 Local Beam Search도 여전히 "Local Maximum"의 문제를 완전히 해결한 것은 아니다

state의 개수가 많고 병렬적으로 탐색한다고 해도 각 state의 value가 모두 독립적이라는 보장은 없고 나중에 각 state가 전부 동일한 state라면 결론적으로 동일한 path일 가능성이 존재한다

4) Genetic Algorithms (GA)

생태계를 생각해보면 우월한 유전자일수록 후손들을 남길 확률이 당연히 높아지고 품질이 안좋은 유전자는 후대에 도태될 가능성이 높다 >> "적자생존"

"후손을 생성"한다는 개념은 "두 부모"로부터 random %로 각각 유전자를 받게 되고 "여기서 돌연변이가 발생할 가능성" 또한 존재한다

계속 후대로 갈 수록 각 state들은 환경에 더 적합하도록 진화가 된다

GA도 마찬가지로 "K"개의 random하게 생성된 state들이 존재한다
>> GA에서 state들을 "Population 집단"이라고 한다

이 때 GA에서 가장 중요한 점은 "각 state들이 String으로 Encoding"되었다는 점이다

여기서 "24748552", "32752411", "24415124" 이러한 String들을 "염색체"라고 한다
그리고 "24748552"에서 각 bit인 2, 4, 7, 4, ... 이러한 것들을 "유전자"라고 한다

"다음 세대"를 생성할 때는 "Genetic Operators"에 의해서 생성된다

→ Selection (선택)

이전 세대의 state를 평가 한 후, 우수한 state들을 선택해서 선택한 state를 이용해서 어떠한 과정들을 통해서 새로운 세대를 생성

→ Crossover (교배)

Selection을 통해서 선택된 state 쌍들을 서로서로 유전자 교환에 의해서 자손을 쌍으로 생성

→ Mutation (돌연변이)

이유 모르게 유전정보가 다르게 변경됨

>> 이렇게 생성된 후손은 모든 후손이 이전 세대보다 좋아지는 것은 아니지만 GA는 "기존 세대의 Best보다는 새로운 세대의 Best가 더 좋다"라는 것을 가정하고 보장한다

(a) 초기 집단

초기 집단은 random하게 생성이 된다

(b) 적합도 함수

Fitness Function을 정의할 때 N-Queens를 활용한다
각 state에 대한 "상태 평가 value"는 "충돌 하지 않는 쌍의 개수"로 구해준다

여기서 충돌하지 않는 쌍의 개수는 "24"이다
따라서 "24748552"의 상태 평가 value는 "24"가 된다

나머지 state들도 마찬가지로 구해주면 된다

4개의 state에 대한 상태 평가 value는 다음과 같다

"24748552" : 24
"32752411" : 23
"24415124" : 20
"32543213" : 11

물론 숫자를 사용할 수 있지만 숫자에 대한 정규화 과정을 거치면 더 공평한 value가 될 것이다

"24748552" : 31%
"32752411" : 29%
"24415124" : 26%
"32543213" : 14%

(c) 선택

부모 state를 뽑을 때는 물론 가급적 Best State를 뽑으면 더 좋을 것이다
하지만 Best만 뽑으면 "다양성"을 보장해주지 못할 것이다
따라서 가급적 Best를 뽑지만 "균형적"으로 뽑는 것이 중요하다 : Random

Random & "F-F가 높으면 뽑힐 확률 ↑"

여기서 교배를 위한 "Cutting Point"가 존재하는데 "Cutting Point" 또한 "다양성 보장"을 위해서 random으로 잘라버린다

(d) 교배

이렇게 부모 2쌍으로부터 후손 2쌍이 생성 되었다

(e) 돌연변이

하지만 GA에서는 각 State에서 "돌연변이"가 발생할 가능성 또한 존재한다

돌연변이 발생 가능성도 Random
어디 위치에 돌연변이 발생하냐도 Random
무슨 값으로 변경되냐도 Random

이렇게 "Random"을 통해서 "다양성"을 보장하는 것이 GA이다

물론 이렇게 최종적으로 완성된 "다음 세대"는 부모보다 value가 높을 수도 있고 낮을 수도 있다
부모보다 value가 높을 경우에는 다다음 세대에서도 우월한 유전자를 바탕으로 후손을 남길 가능성이 높아진다
하지만 value가 더 낮을 경우에는 다다음 세대에서 도태될 가능성이 높다

Coding -> 블로그 이전

Coding