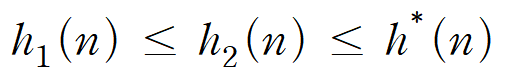2022. 4. 1. 16:38ㆍMajor`/인공지능
Informed Search (= Heuristic Search)
"지식"을 사용해서 여러 갈림길 중 최적의 node를 효율적으로 탐색하는 방법
- Best-First Search
- A* Search
- Iterative Deepening A* (IDA*) Search
Node를 펼쳐놓고 탐색하기 전에 해당 Node가 문제 해결에 있어서 얼마나 좋고 최적의 Node인지 판단해주는 평가함수 : f(n)을 사용
→ 평가함수가 좋은 Node부터 Expanding
Greedy Best-First Search
전체적인 환경에서 각 후보 node(아직 확장 X)들에 대한 우선순위? 특정 Integer값이 존재한다
그리고 각 우선순위는 "지식"을 활용해서 평가를 한다
평가 함수 f(n)은 여러 후보 node들을 평가해준다
평가 방법은 각 node의 Integer값 중 자신에게 주어진 환경에서 얼마나 좋은지 "지식"을 통해서 판단한다 >> Priority Queue
Greedy Best-First Search는 f(n) = h(n)으로 정의한다
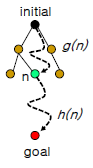
이러한 환경이 주어졌다고 가정하면,
일단 initial ~> n까지는 어떻게 어떻게해서 갔다고 한다
이제 Agent가 판단해야 하는 것은 n -> goal까지 어떤 node를 경유해서 갈것인지를 판단해야 한다

>> 결국 다른의미로 각 후보 node들 중에서 "어느 node가 Goal에 더 가까운가"를 판단하는 문제와 동일하다
당연히 h(n)은 작을수록 좋을 것이다
왜냐면 h(n)은 결국 해당 node : n이 Goal에 얼마나 가까운지를 return해주기 때문이다
Example) Romania Traveling


오른쪽 값들은 h_SLD(n)이고, 각 node에서 Bucharest까지 직선거리를 의미한다

(a)
초기 상태는 Arad에 위치해있다
(b)
이제 Arad로부터 갈 수 있는 node들은 Sibiu / Timisoara / Zerind가 존재한다
각각의 node들에 대한 h_SLD(n)을 보게되면 253 / 329 / 374이다
당연히 Sibiu가 h(n)상으로 가장 작은 값을 return하기 때문에 다음 확장 node는 "Sibiu"가 되었다
>> 계속 동일한 방식으로 expanding하면 결국 Bucharest에 도달할 것이다
| Greedy Best-First Search |
만족? 불만족? | 이유 |
| 완전성 | X | 위의 그림을 보게되면 Sibiu에서 Arad로 되돌아갈 수 있는 것을 볼 수 있다 따라서 indefinite loop가 발생할 수 있다 |
| 최적성 | X | 완전성이 보장이 되지 않음으로 최적성 또한 보장이 되지 않는다 |
| 시간 복잡도 | O(bm) | |
| 공간 복잡도 | O(bm) | |
A* Search
위의 Best-First Search는 "f(n) = h(n)"으로 정의했고, 그에 따라서 node들을 확장한다
A* Search는 f(n)의 정의가 Best-First Search와는 다르다
"f(n) = g(n) + h(n)"
Best-First Search는 현재 node n에 대해서 initial로부터 n까지 어떤 cost를 가지고 왔는지는 관심이 없고 오직 n -> goal만 관심이 있다
A* Search는 현재 node n까지 어떻게 왔고 : g(n), 이제 n -> goal까지 : h(n) 어떤 경로로 최소 cost를 통해서 갈 수 있을까이므로 둘다 고민해야 한다
- g(n) : 실제 cost
- h(n) : 추정 cost (estimated cost)
- f(n) : 추정 cost (estimated cost)

따라서 A* Search는 "현재 node까지 어떻게 왔냐"도 중요한 문제이다

(b) → (c)의 과정은 아직 확장되지 않은 노드중에서 Fagaras가 가장 작기 때문에 Fagaras를 확장한 것이다
(c)에서는 확장되지 않은 9개의 노드중에서 Pitesti가 가장 작기 때문에 Pitesti를 확장한다
fagaras에서 bucharest로 갈 수 있지만 A*에서는 목적지가 도출되었어도 이보다 좋은 path cost가 존재하는지 더 찾으려는 노력을 한다
A* Search는 Arad -> Bucharest까지 "418 cost"가 들었지만
Best-First Search는 Arad -> Bucharest까지 "450 cost"가 들었다
| <A* Search> | 만족? 불만족? | 이유 |
| 완전성 | O | 온것 + 갈것의 비용을 전부 고려하기 때문에 완전성 & 최적성 둘다 보장된다 |
| 최적성 | O | |
| 시간 복잡도 | O(bd) | |
| 공간 복잡도 | O(bd) | |
A* Search의 조건
1) Admissible Heuristic (Heuristic Function을 허용할 수 있는가)
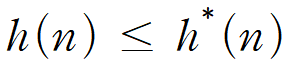
h(n)은 node → goal까지 예측한 cost이다 :: 직선거리
h*(n)은 node → goal까지 실제 cost이다
예측값은 반드시 실제값보다 작거나 같아야 한다 : Never Overestimate / Always Underestimate
예측값이 더 작으면 허용 O
예측값이 더 크면 허용 X
만약 h(n)이 Admissible하다면 A*를 활용한 Tree Search는 반드시 최적성을 보장한다
※ Example) 8-puzzle
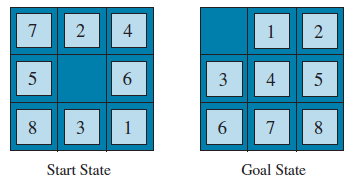
h1(n) : 잘못 배치된 tile의 수
1, 2, 3, 4, 5, 6, 7, 8 모두 잘못되어 있다
- h1(n) = 8
h2(n) : Manhatten Distance (=Left/Right/Up/Down을 통해서 원래 자리로 되돌아갈 때 소요되는 cost)
1 : RDD = 3
2 : L = 1
3 : LU = 2
4 : RU = 2
5 : LL = 2
6 : RRU = 3
7 : LUU = 3
8 : LL = 2
- h2(n) = 3 + 1 + 2 + 2 + 2 + 3 + 3 + 2 = 18
>> 당연히 실제로 옮길 때는 각 tile별로 독립적이지 않기 때문에 더 많은 cost가 발생할 것이다 :: Admissible Heuristic 만족
2) Dominance (어느 Heuristic Function이 더 우수한가)
두 예측함수 h1(n), h2(n)이 Admissible하다고 가정하면
h2(n) ≥ h1(n)일 경우 :: "h2 dominates h1" (h2가 h1보다 우수)