2022. 3. 12. 19:51ㆍMajor`/알고리즘
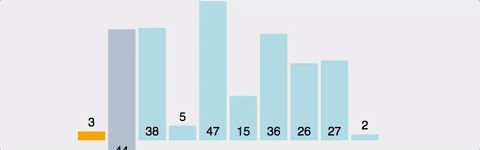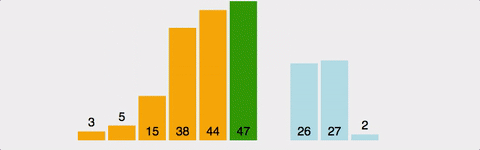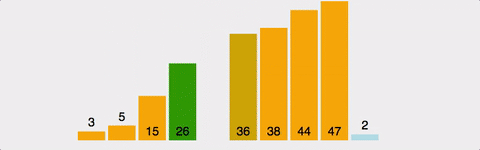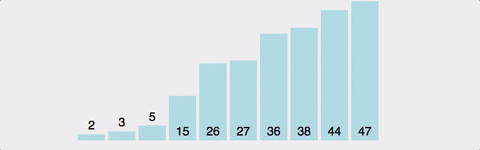

Stable Sort
정렬 방식
- 두번째 값부터 차례대로 해당 값을 넣을 위치를 전체적인 배열의 자리에서 결정해준다
>> 선택한 값의 "앞에 요소들"을 살펴보고 만약 앞에 요소들 중 자신보다 큰 값이 있다?? 그러면 앞에 요소들을 차례대로 오른쪽으로 shift 해준다
| 9 | 17 | 1 | 2 | 12 | 6 |
▶ Round 1 (index 1)
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 9 | 17 | 1 | 2 | 12 | 6 |
- "index(1) 17"앞에는 "9"라는 값이 있다
- 9는 17보다 작다
- 따라서, 여기서는 shift 해줄 필요가 없다
▶ Round 2 (index 2)
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 9 | 17 | 1 | 2 | 12 | 6 |
- insert하려는 기준 값 = "index(2) : 1"
- 해당 값 이전의 요소들을 알아봐야 한다 >> index = i - 1 = 1
- index(1) : 17은 insert하려는 기준 값 "1"보다 크다 >> 따라서, index를 1 감소시키고 (1 → 0), "17"을 우측으로 1칸 shift
- index(0) : 9는 insert하려는 기준 값 "1"보다 크다 >> 따라서, index를 1 감소시키고 (0 → -1), "9"를 우측으로 1칸 shift
>> 여기서 index가 -1이 되었으니까 +1을 해주고 해당 index에 insert하려는 기준값을 넣어주기
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 1 | 9 | 17 | 2 | 12 | 6 |
▶ Round 3 (index 3)
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 1 | 9 | 17 | 2 | 12 | 6 |
- 위와 동일한 방법으로 index를 감소시켜주면서 이전 값들을 shift해주기
index 변화 : 2 → 1 → 0 (여기서 + 1을 통해서 최종적으로 기준값을 insert하려는 index 가리키기)
shift : 9, 17을 우측으로 shift
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 1 | 2 | 9 | 17 | 12 | 6 |
▶ Round 4 (index 4)
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 1 | 2 | 9 | 17 | 12 | 6 |
index 변화 : 3 → 2 (+1을 통해서 최종적으로 기준값을 insert하려는 index 가리키기)
shift : 17을 우측으로 shift
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 1 | 2 | 9 | 12 | 17 | 6 |
▶ Round 5 (index 5)
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 1 | 2 | 9 | 12 | 17 | 6 |
index 변화 : 4 → 3 → 2 → 1 (+1을 통해서 최종적으로 기준값을 insert하려는 index 가리키기)
shift : 9, 12, 17을 우측으로 shift
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| 요소 | 1 | 2 | 6 | 9 | 12 | 17 |
>> 최종적으로 정렬이 완료되었다
Java Code
static void insertion_sort_while(int [] list, int n){
for(int i = 1; i < n; i++){
int key = list[i]; // insert 하려는 기준 값
int index = i - 1; // 이전 값들과 비교
while(index >= 0 && list[index] > key){
list[index + 1] = list[index];
index--;
}
list[index + 1] = key;
}
}
static void insertion_sort_for(int [] list, int n){
for(int i = 1; i < n; i++){
int key = list[i];
for(int j = i - 1; j >= 0 && list[j] > key; j--){
list[j + 1] = list[j];
list[j] = key;
}
}
}while문은 index를 최종적으로 결정해서 해당 index에 key를 넣는 방식
for문은 index가 결정될때마다 key를 넣는 방식
시간복잡도 분석 (for문 & 상수는 C로 간주 & Worst Case 기준)
1) 가장 안쪽 for문부터 분석
for(int j = i - 1; j >= 0 && list[j] > key; j--){
list[j + 1] = list[j];
list[j] = key;
}- for문 내에 연산 개수 : C개 (상수)
- for문 루프 횟수 : (i-1)+1 = i번
>> C1i
2) 바깥쪽 for문 분석
for(int i = 1; i < n; i++){
int key = list[i];
for(int j = i - 1; j >= 0 && list[j] > key; j--){
list[j + 1] = list[j];
list[j] = key;
}
}- for문 내 연산 개수 : C1i + C2
3) 최종 시간복잡도

Example Code
package Sort;
/*
1) 2 ~ n까지 반복 (i)
2) i보다 작은 index들에 대해서 해당 index 값이 i보다 크다? 그러면 shift
*/
// Shift 방식
public class Insertion_Sort_9 {
public static void main(String[] args) {
int [] list = new int[30]; // 정렬할 배열 A
for(int i=0; i<list.length; i++)
list[i] = (int)(Math.random()*201); // 0~200
// 정렬 전 list 출력
System.out.print("정렬 전 list []");
for(int i=0; i<list.length; i++){
if(i%10==0) System.out.println();
System.out.print(list[i] + "\t");
}
System.out.println("\n");
insertion_sort_for(list, list.length);
// 정렬 후 list 출력
System.out.print("정렬 후 list []");
for(int i=0; i<list.length; i++){
if(i%10==0) System.out.println();
System.out.print(list[i] + "\t");
}
System.out.println("\n");
}
static void insertion_sort_while(int [] list, int n){
for(int i = 1; i < n; i++){
int key = list[i]; // insert 하려는 기준 값
int index = i - 1; // 이전 값들과 비교
while(index >= 0 && list[index] > key){
list[index + 1] = list[index];
index--;
}
list[index + 1] = key;
}
}
static void insertion_sort_for(int [] list, int n){
for(int i = 1; i < n; i++){
int key = list[i];
for(int j = i - 1; j >= 0 && list[j] > key; j--){
list[j + 1] = list[j];
list[j] = key;
}
}
}
}
