[Data Structure] 히프 정렬 - Heap Sort

히프 정렬 (Heap Sort)

Unstable Sort

• 완전이진트리 구조
• 배열을 이용해서 구현 or 컬렉션을 통해서 구현

 

시간복잡도

- O(n log n) 

 

장점

- 추가 메모리가 필요없고 항상 O(n log n)의 시간복잡도를 가진다

 

단점

- 보통의 경우, 퀵정렬보다 느리다

• 데이터의 상태에 따라서 다른 정렬들에 비해 조금 느리다

- 안정성을 보장받지 못한다

 

과정

- 최대힙 : 힙에서 pop시킨 요소를 배열의 뒤에서부터 채운다

- 최소힙 : 힙에서 pop시킨 요소를 배열의 앞에서부터 채운다

• C : 직접 구현
• Java : PriorityQueue / 직접 구현
• Python : heapq / PriorityQueue / 직접 구현

 

 

▶ PriorityQueue 이용

PriorityQueue<Integer> pq1 = new PriorityQueue<>(); // 최소 힙
PriorityQueue<Integer> pq2 = new PriorityQueue<>(Collections.reverseOrder()); // 최대 힙

static void min_heap(int[]A1, PriorityQueue<Integer> pq1){
        for(int i=0; i<A1.length; i++)
            A1[i] = pq1.poll();
    }

static void max_heap(int[]A2, PriorityQueue<Integer> pq2){
        for(int i=A2.length-1; i>=0; i--)
            A2[i] = pq2.poll();
    }

 

 

▶ 직접 Heap 구현

class Heap{
    private int maxsize, heap_size;
    private int [] heap;

    Heap(int maxsize){
        this.maxsize = maxsize;
        this.heap_size = 0;
        heap = new int[maxsize];
    }
    boolean is_full(){
        return heap_size == maxsize;
    }
    boolean is_empty(){
        return heap_size == 0;
    }
    void insert(int num){
        if(is_full()) return;
        else{
            int index = ++heap_size;
            while(index != 1 && (num > heap[index/2])){
                heap[index] = heap[index/2];
                index/=2;
            }
            heap[index] = num;
        }
    }
    int delete(){
        if(is_empty()) return 0;
        else{
            int root = heap[1];
            int last = heap[heap_size--];
            int index = 1;
            int child = 2;
            while(child<=heap_size){
                if((child<heap_size) && (heap[child] < heap[child+1]))
                    child++;
                if(last>=heap[child]) break;
                heap[index] = heap[child];
                index = child;
                child*=2;
            }
            heap[index] = last;
            return root;
        }
    }
}

static void heap_sort(Heap heap, int[] result){
        for(int i=result.length-1; i>=0; i--)
            result[i] = heap.delete();
    }

 

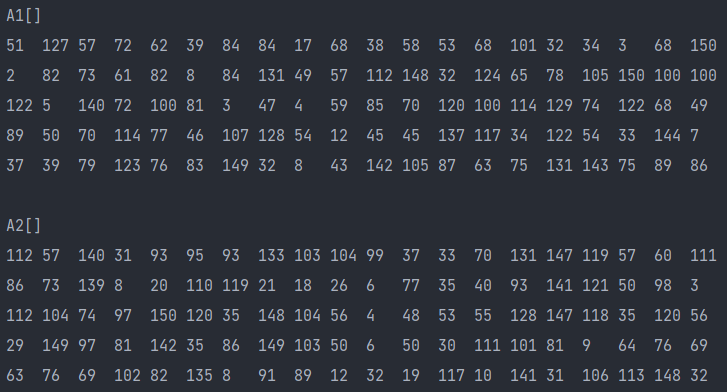
▶ PriorityQueue 결과

 

 

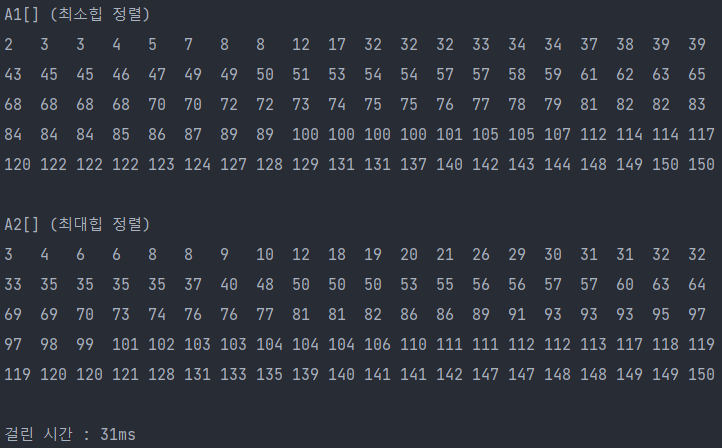
▶ 직접 Heap 구현 결과