[Data Structure] 최소 신장 트리 - Prim MST Algorithm
2021. 12. 25. 12:28ㆍMajor`/자료구조
Prim MST Algorithm
- 시작 정점에서부터 신장 트리 집합을 확장해가는 알고리즘
- 인접 정점들 중에서 가중치가 최소인 정점을 선택해가면서 트리를 확장
- 이전 단계에서 만들어진 신장 트리를 확장
- n개의 정점에 대해서 n-1개의 간선을 선택하면 알고리즘 종료
- 배열로 구현 or 최소히프로 구현
- 어떤 정점에서 시작하던간에 똑같은 트리 생성
- O(n²)
※ 각 정점으로부터 거리 distance 배열, 선택된 정점 selected 배열 (모든 정점 distance = INF로 초기화)
- v의 인접 정점들 distance 업데이트
- 인접 정점들 중 distance가 가장 낮은 정점(w) 선택
- v와 w를 하나의 그룹으로 간주하고 해당 그룹으로부터 distance 다시 업데이트
- n-1개 간선 선택할 때 까지 1~4 반복

※ Example

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| selected | |||||||
| distance | INF | INF | INF | INF | INF | INF | INF |

- 정점 0 선택
- 0의 인접 정점 {1, 3, 4}의 distance 업데이트
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| selected | |||||||
| distance | 15 | INF | 54 | 24 | INF | INF |
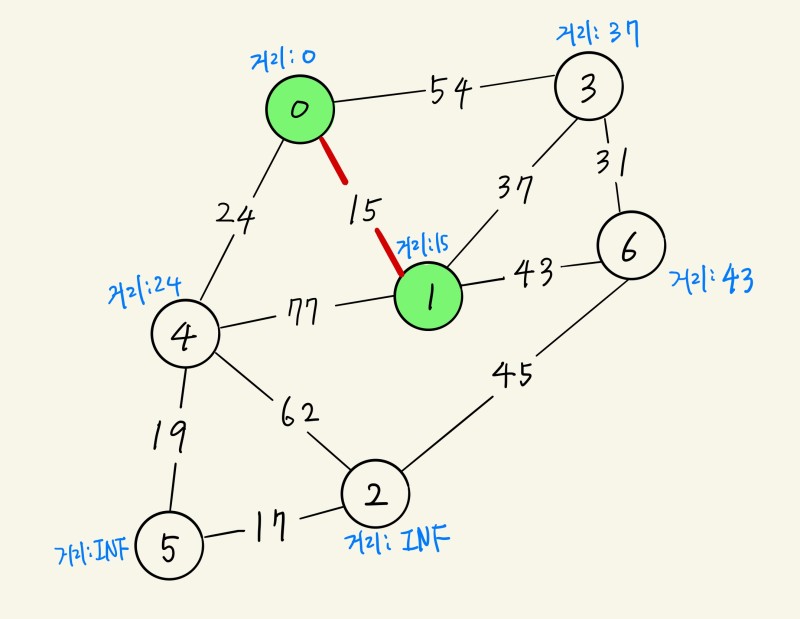
- 0에서 가중치가 가장 작은 정점 1 선택
- (0, 1)을 하나의 그룹으로 간주하고 해당 그룹의 인접 정점 {3, 4, 6}의 distance 업데이트
- 원래 저장된 distance와 새로 계산된 해당 그룹의 distance를 비교해서 더 작은 값 저장
| 2 | 3 | 4 | 5 | 6 | |||
| selected | |||||||
| distance | INF | 37 | 24 | INF | 43 |

- (0, 1)에서 가중치가 가장 작은 정점 4 선택
- (0, 1, 4)를 하나의 그룹으로 간주하고 해당 그룹의 인접 정점 {2, 3, 5, 6}의 distance 업데이트
| 2 | 3 | 5 | 6 | ||||
| selected | |||||||
| distance | 62 | 37 | 19 | 43 |

- (0, 1, 4)에서 가중치가 가장 작은 정점 5 선택
- (0, 1, 4, 5)를 하나의 그룹으로 간주하고 해당 그룹의 인접 정점 {2, 3, 6}의 distance 업데이트
| 2 | 3 | 6 | |||||
| selected | |||||||
| distance | 17 | 37 | 43 |

- (0, 1, 4, 5)에서 가중치가 가장 작은 정점 2 선택
- (0, 1, 2, 4, 5)를 하나의 그룹으로 간주하고 해당 그룹의 인접 정점 {3, 6}의 distance 업데이트
| 3 | 6 | ||||||
| selected | |||||||
| distance | 37 | 43 |

- (0, 1, 2, 4, 5)에서 가중치가 가장 작은 정점 3 선택
- (0, 1, 2, 3, 4, 5)를 하나의 그룹으로 간주하고 해당 그룹의 인접 정점 {6}의 distance 업데이트
| 6 | |||||||
| selected | |||||||
| distance | 31 |

- (0, 1, 2, 3, 4, 5)에서 가중치가 가장 작은 정점 6 선택
- 정점이 총 7개이고, 현재 선택된 간선은 6개이므로 즉시 알고리즘 종료
| selected | |||||||
| distance |
▶ Prim Algorithm Code
int get_min_weight(int n) {
// n = g->n
int v; // 선택된 정점 (현재 그룹으로부터 weight가 가장 작은 정점)
for (int i = 0; i < n; i++) {
if (selected[i] == FALSE)
v = i;
}
for (int i = 0; i < n; i++) {
if (selected[i] == FALSE && distance[i] < distance[v])
v = i;
}
return v;
}Code 4~6
- 모든 정점들에 대해 selected - FALSE인 정점 선택
Code 8~10
- Code 4~6에서 선택된 정점보다 distance가 더 작은 정점을 최종적으로 선택해서 return
void prim_mst(graph* g, int v) {
// v = 시작 정점
init_distance(distance);
init_selected(selected);
distance[v] = 0; // 시작 정점 ~ 시작 정점은 당연히 distance = 0
int cost = 0; // 비용 -> vertex가 추가될 때마다 누적
for (int i = 0; i < g->n; i++) {
int s = get_min_weight(g->n); // 선택된 정점( weight minimum )
selected[s] = TRUE;
cost += distance[s];
printf("\n");
printf(">> 정점 %d 추가 -> 현재 비용 : %d\n\n", s, cost);
printf("distance UPDATE\n>> ");
for (int i = 0; i < g->n; i++) {
if(distance[i] == INF)
printf(" V%d : %s\t", i, "INF");
else
printf(" V%d : %d\t", i, distance[i]);
}
printf("\n");
printf("select UPDATE\n>> ");
for (int i = 0; i < g->n; i++) {
if (selected[i] == TRUE)
printf(" V%d : %s\t", i, "TRUE");
else
printf(" V%d : %s\t", i, "FALSE");
}
printf("\n--------------------------------------------");
for (int w = 0; w < g->n; w++) {
// w = 선택된 s의 인접 정점
if (g->weight[s][w] != INF) {
if (selected[w] == FALSE && g->weight[s][w] < distance[w]) {
distance[w] = g->weight[s][w];
}
}
}
}
printf("\n최종 비용 : %d\n", cost);
}Code 3~4
- 각 정점들의 distance, selected를 각각 INF, FALSE로 초기화
Code 6~7
- prim_mst함수의 매개변수 v는 시작 정점을 의미한다
- 시작정점의 distance는 당연히 0으로 설정
- cost = 정점을 지나갈 때마다 누적되는 비용
Code 10~12
- 현재 그룹으로부터 distance가 가장 작은 정점(w)을 선택하고, 해당 정점을 selected - TRUE 표시
- → 처음에는 시작정점(v)말고, 다른 정점은 모두 distance가 INF이기 때문에 처음에는 매개변수인 시작정점 v를 선택
- 현재 그룹 ~ 선택된 정점까지의 distance를 cost에 누적
Code 34~38
- Code 10~12에서 선택된 정점 s로부터 distance가 INF가 아닌 모든 정점들에 대상
- w가 아직 selected - FALSE이고, 원래 w의 distance보다 s~w의 distance가 더 작으면 (distance[w] < weight[s][w]) 원래 w의 distance를 새롭게 update
Full Code
#include <stdio.h>
#include <stdlib.h>
// Prim MST Algorithm //
#define TRUE 1
#define FALSE 0
#define MAX_VERTEX 100
#define INF 99999
int selected[MAX_VERTEX]; // 정점이 선택되면 해당 정점은 TRUE로 / 처음에는 FALSE로 전부 초기화
int distance[MAX_VERTEX]; // 그룹으로부터 각 정점까지의 거리 / 처음에는 INF로 전부 초기화
void init_distance(int distance[]) {
for (int i = 0; i < MAX_VERTEX; i++)
distance[i] = INF;
}
void init_selected(int selected[]) {
for (int i = 0; i < MAX_VERTEX; i++)
selected[i] = FALSE;
}
typedef struct graph {
int n; // 정점 개수
int vertex[MAX_VERTEX];
int weight[MAX_VERTEX][MAX_VERTEX];
}graph;
graph* create() {
return (graph*)malloc(sizeof(graph));
}
void init_graph(graph* g) {
g->n = 0;
for (int r = 0; r < MAX_VERTEX; r++) {
for (int c = 0; c < MAX_VERTEX; c++) {
g->weight[r][c] = INF;
}
}
}
int is_full(graph* g) {
return g->n == MAX_VERTEX;
}
int bool_vertex(graph* g, int v) {
int flag = FALSE;
for (int i = 0; i < g->n; i++) {
if (g->vertex[i] == v)
flag = TRUE;
}
if (flag == TRUE) return TRUE;
else return FALSE;
}
void insert_vertex(graph* g, int v) {
if (is_full(g))
return;
else if (bool_vertex(g, v) == TRUE)
return;
g->vertex[g->n++] = v;
}
void insert_edge(graph* g, int start, int end, int weight) {
// 무방향 그래프를 조건으로
if (bool_vertex(g, start) == FALSE || bool_vertex(g, end) == FALSE)
return;
g->weight[start][end] = weight;
g->weight[end][start] = weight;
}
int get_min_weight(int n) {
int min = INF;
int v = 0;
for (int i = 0; i < n; i++) {
if (selected[i] == FALSE && distance[i] < min) {
min = distance[i];
v = i;
}
}
return v;
}
void prim_mst(graph* g, int v) {
// v = 시작 정점
init_distance(distance);
init_selected(selected);
distance[v] = 0; // 시작 정점 ~ 시작 정점은 당연히 distance = 0
int cost = 0; // 비용 -> vertex가 추가될 때마다 누적
for (int i = 0; i < g->n; i++) {
int s = get_min_weight(g->n); // 선택된 정점( weight minimum )
selected[s] = TRUE;
cost += distance[s];
printf("\n");
printf(">> 정점 %d 추가 -> 현재 비용 : %d\n\n", s, cost);
for (int w = 0; w < g->n; w++) {
// w = 선택된 s의 인접 정점
if (g->weight[s][w] != INF) {
if (selected[w] == FALSE && g->weight[s][w] < distance[w]) {
distance[w] = g->weight[s][w];
}
}
}
printf("distance UPDATE\n>> ");
for (int i = 0; i < g->n; i++) {
if(distance[i] == INF)
printf(" V%d : %s\t", i, "INF");
else
printf(" V%d : %d\t", i, distance[i]);
}
printf("\n");
printf("select UPDATE\n>> ");
for (int i = 0; i < g->n; i++) {
if (selected[i] == TRUE)
printf(" V%d : %s\t", i, "TRUE");
else
printf(" V%d : %s\t", i, "FALSE");
}
printf("\n--------------------------------------------");
}
printf("\n최종 비용 : %d\n", cost);
}
int main(void) {
graph* g;
g = create(); init_graph(g);
for (int i = 0; i < 7; i++)
insert_vertex(g, i);
insert_edge(g, 0, 1, 15);
insert_edge(g, 0, 3, 54);
insert_edge(g, 0, 4, 24);
insert_edge(g, 1, 3, 37);
insert_edge(g, 1, 4, 77);
insert_edge(g, 1, 6, 43);
insert_edge(g, 2, 4, 62);
insert_edge(g, 2, 5, 17);
insert_edge(g, 2, 6, 45);
insert_edge(g, 3, 6, 31);
insert_edge(g, 4, 5, 19);
printf("--------------------------------------------\n");
printf("Prim MST Algorithm\n");
printf("V : {0, 1, 2, 3, 4, 5, 6}\n");
printf("E : {(0, 1, 15), (0, 3, 54), (0, 4, 24), (1, 3, 37), (1, 4, 77), (1, 6, 43), (2, 4, 62), (2, 5, 17), (2, 6, 45), (3, 6, 31), (4, 5, 19)}\n");
printf("--------------------------------------------");
prim_mst(g, 0);
return 0;
}

