[Data Structure] 우선순위 큐 (히프)

우선순위 큐 (priority queue)

- 일반적인 큐 : FIFO(First In First Out)구조

- 우선순위 큐 : 우선순위가 높은 데이터가 먼저 나간다

• 시뮬레이션 시스템, 네트워크 트래픽 제어, 작업 스케쥴링, 수치해석계산 등에 사용

자료구조	삭제되는 요소
Stack	가장 늦게 들어온 데이터 (LIFO)
Queue	가장 먼저 들어온 데이터 (FIFO)
Priority Queue	가장 우선순위가 높은 데이터 (Priority)

 

구현 방법

배열 / 연결 리스트 / 히프

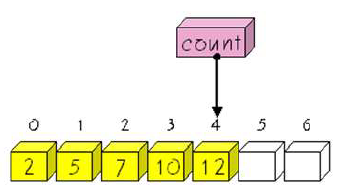
- 배열 / 연결리스트 / 히프 

표현 방법	삽입	삭제
정렬 안된 배열/연결 리스트	O(1)	O(n)
정렬 된 배열/연결 리스트	O(n)	O(1)
힙	O(log n)	O(log n)

- 만약 n이 1000일 경우

• O(n) : 1000초 / O(log₂n) : 10초

∴ 힙의 효율은 배열/연결 리스트보다 훨씬 좋다

---

힙 (Heap)

- 완전 이진 트리 기반 

- 배열을 이용해서 구현

- 여러 개의 값들 중에 max, min을 빠르게 찾아내도록 설계된 자료구조

• 힙트리는 이진탐색트리와 달리, 중복된 값을 허용한다
• 힙 안에서 데이터들은 느슨한 정렬 상태를 유지
• 힙의 목적 : delete 연산 시, 가장 큰 값 찾아내기 → 전체를 정렬할 필요가 없다 

 

 

힙의 종류

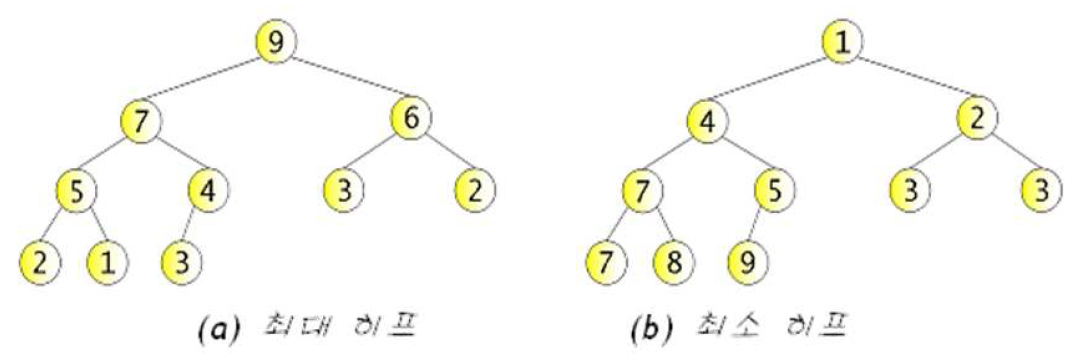
▶ 최대 힙

• key(부모 노드) ≥ key(자식 노드)

▶ 최소 힙

• key(부모 노드) ≤ key(자식 노드)

 

---

 

힙 구현 (최대 힙)

- 각 노드(레벨 별로) 번호 부여 (루트 노드 = 1)

- 각각의 번호를 배열의 인덱스라고 설정하고 구현

 

※ 인덱스 (부모↔자식)

• 왼쪽 자식 인덱스 = (부모 인덱스)×2
• 오른쪽 자식 인덱스 = (부모 인덱스)×2 + 1
• 부모 인덱스 = (자식 인덱스)/2

 

 

1. 삽입 연산

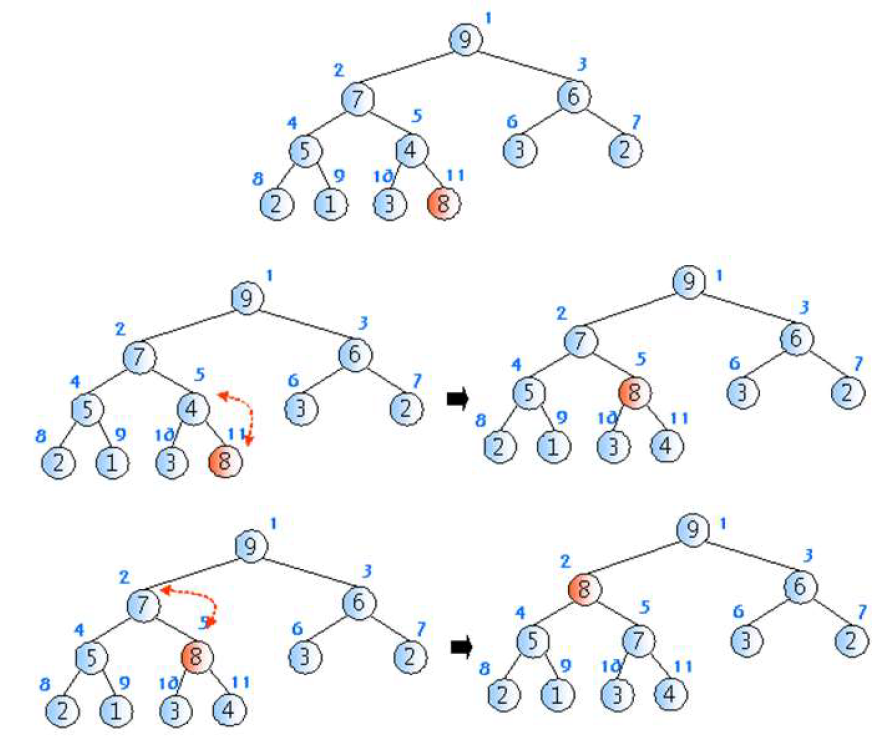
1. item이 들어갈 인덱스 = 현재 히프트리에 있는 최종 item 인덱스의 다음 인덱스

2. 만약, item이 해당 item의 부모 item보다 크면 (item > item의 부모 item) 

• item이 들어갈 인덱스(i)에 부모 item을 할당 -- (1)
• item이 들어갈 인덱스(i)를 부모 인덱스로 update : (i/2) -- (2)
  • item 인덱스(i)가 해당 인덱스의 부모 인덱스보다 작아질 때 까지 (1), (2) 반복

void insert_node(heapnode* h, element item) {
	if (is_full(h)) {
		fprintf(stderr, "Error : Heap is full\n\n");
		return;
	}
	else {
		int i; // item의 인덱스
		i = ++h->heap_size;
		// item인덱스 = 현재 히프트리에 있는 최종 item 인덱스의 다음 인덱스
		while (i != 1 && (item > h->heap[i / 2])) {
			h->heap[i] = h->heap[i / 2];
			i /= 2;
		}
		h->heap[i] = item;
	}
}

 

 

2. 삭제 연산

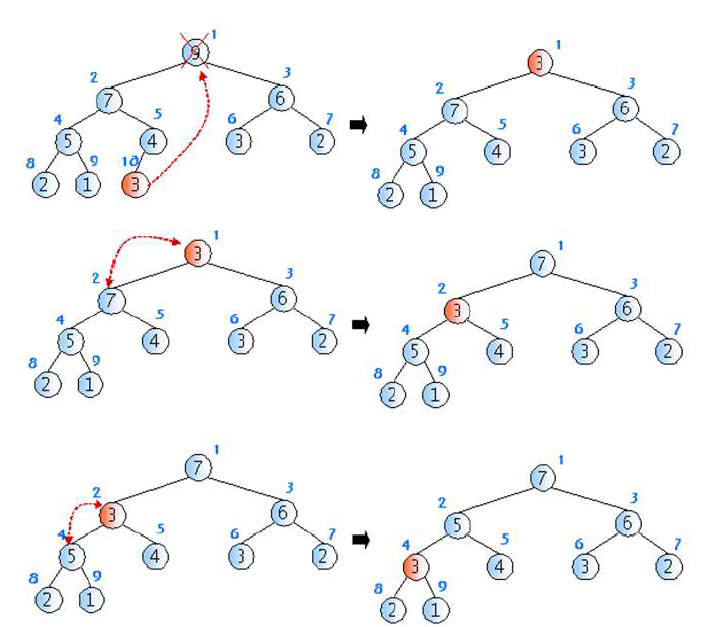
1. 루트 노드를 삭제시키고, 말단 노드를 루트도 옮기기 (루트에 말단 노드의 item 저장)

2. root의 자식들과 root의 값을 비교해서 -- (1)

• root 값 < root자식들 값 : 자식들 중 큰 값을 선택해서 root노드와 교체 -- (2)
  • root값 > root 자식들 값이 될 때 까지 (1), (2) 반복

element delete_node(heapnode* h) {
	if (is_empty(h)) {
		fprintf(stderr, "Error : Heap is empty\n\n");
		return;
	}
	else {
		element root = h->heap[1]; // 루트 노드 item
		element last = h->heap[h->heap_size--]; // 말단 노드 item
		// 루트 노드를 삭제시키고 말단을 루트로 올릴거기 때문에 heap_size는 1 감소
		int index = 1; // 말단 노드가 들어가는 index -> 자리 찾을 때 까지 계속 변함
		int child = 2;
		while (child <= h->heap_size) {
			if ((child < h->heap_size) && (h->heap[child] < h->heap[child + 1]))
				child++; // 자식 노드 중 더 큰 값의 인덱스 찾기
			if (last >= h->heap[child]) break;
			// 최종 insert 노드의 값이 해당 인덱스의 자식 값보다 크면 더 이상 옮기기 X
			h->heap[index] = h->heap[child];
			index = child;
			child *= 2;
		}
		h->heap[index] = last;
		return root;
	}
}

 

 

3. Full Code (Heap)

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <ctype.h>
// 배열로 히프 구현

#define MAX_HEAP_SIZE 100

// 밑이 2인 로그함수
double logB(int x, int base) {
	return (double)log(x) / log(base);
}

typedef int element; // heap의 요소 type
typedef struct headnode {
	int heap_size;
	element heap[MAX_HEAP_SIZE];
}heapnode;

heapnode* create() {
	return (heapnode*)malloc(sizeof(heapnode));
}

void init_heap(heapnode* h) {
	h->heap_size = 0;
}

int heap_length(heapnode* h) {
	// heap에 있는 item 개수
	return h->heap_size;
}

int is_empty(heapnode* h) {
	return h->heap_size == 0;
}

int is_full(heapnode* h) {
	return h->heap_size == MAX_HEAP_SIZE - 1;
}

void insert_node(heapnode* h, element item) {
	if (is_full(h)) {
		fprintf(stderr, "Error : Heap is full\n\n");
		return;
	}
	else {
		int i; // item의 인덱스
		i = ++h->heap_size;
		// item인덱스 = 현재 히프트리에 있는 최종 item 인덱스의 다음 인덱스
		while (i != 1 && (item > h->heap[i / 2])) {
			h->heap[i] = h->heap[i / 2];
			i /= 2;
		}
		h->heap[i] = item;
	}
}

element delete_node(heapnode* h) {
	if (is_empty(h)) {
		fprintf(stderr, "Error : Heap is empty\n\n");
		return;
	}
	else {
		element root = h->heap[1]; // 루트 노드 item
		element last = h->heap[h->heap_size--]; // 말단 노드 item
		// 루트 노드를 삭제시키고 말단을 루트로 올릴거기 때문에 heap_size는 1 감소
		int index = 1; // 말단 노드가 들어가는 index -> 자리 찾을 때 까지 계속 변함
		int child = 2;
		while (child <= h->heap_size) {
			if ((child < h->heap_size) && (h->heap[child] < h->heap[child + 1]))
				child++; // 자식 노드 중 더 큰 값의 인덱스 찾기
			if (last >= h->heap[child]) break;
			// 최종 insert 노드의 값이 해당 인덱스의 자식 값보다 크면 더 이상 옮기기 X
			h->heap[index] = h->heap[child];
			index = child;
			child *= 2;
		}
		h->heap[index] = last;
		return root;
	}
}

void clear(heapnode* h) {
	h->heap_size = 0;
}

void print_heap(heapnode* h) {
	if (is_empty(h)) {
		fprintf(stderr, "Error : Heap is empty\n\n");
		return;
	}
	for (int i = 1; i <= heap_length(h); i++) {
		printf("[%d]  ", h->heap[i]);
		if (logB(i + 1, 2) - (int)logB(i + 1, 2) == 0) {
			// 1 2 4 8,.. 2의 제곱 때마다 개행
			printf("\n");
		}
	}
	printf("\n\n");
}

int main(void) {
	heapnode* h;
	h = create();
	init_heap(h);

	print_heap(h);
	printf(">> 1~6을 Heap_Tree에 insert\n");
	for (int i = 1; i <=6; i++)
		insert_node(h, i);
	print_heap(h);
	printf(">> 10 insert\n"); insert_node(h, 10); print_heap(h);
	printf(">> 2 insert\n"); insert_node(h, 2); print_heap(h);
	printf(">> 9 insert\n"); insert_node(h, 9); print_heap(h);
	printf(">> delete()\n>> delete된 값 : %d\n", delete_node(h)); print_heap(h);
	printf(">> delete()\n>> delete된 값 : %d\n", delete_node(h)); print_heap(h);
	printf(">> Heap_Tree clear()\n"); clear(h); print_heap(h);
	printf(">> 10 insert\n"); insert_node(h, 10); print_heap(h);
	printf(">> 2 insert\n"); insert_node(h, 2); print_heap(h);
	printf(">> 9 insert\n"); insert_node(h, 9); print_heap(h);
}