[Algorithm Week_3] QuickSort

QuickSort

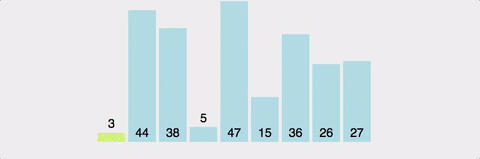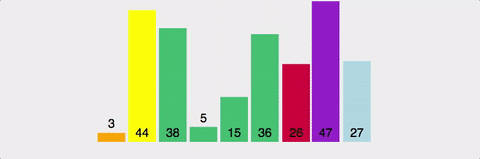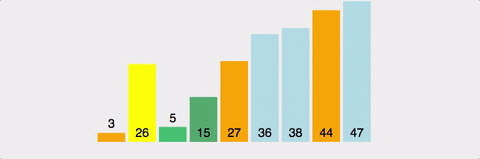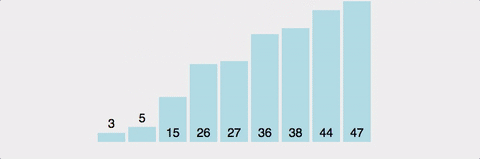
Unstable Sort

---

Recursion으로 생각?

1. 배열의 원소중 "pivot" 고르기

2. pivot을 기준으로 1) pivot보다 작은 값들은 pivot의 왼쪽으로, 2) pivot보다 큰 값들은 pivot의 오른쪽으로 분류시킨다 :: Partition

3. pivot을 기준으로 분류된 두 subarray를 각각 정렬한다 "By Recursion"

• recurse Left
• recurse Right

 

※ MergeSort와 QuickSort의 차이점

MergeSort

- 일단 Recursion을 던져놓고, "Merge"를 통해서 최종적으로 정렬

• 더 상세히 살펴보면, MergeSort는 array의 요소가 1개가 남을때까지 계속해서 subarray들을 반으로 나누고, 다 나누었으면 각 subarray들을 "Merge"함으로써 최종적인 정렬이 완료된다

QuickSort

- 먼저 pivot을 기준으로 요소들을 정리하고 이 다음에 Recursion을 던진다

• 더 상세히 살펴보면, QuickSort는 일단 pivot을 기준으로 "더 작은값/더 큰값"으로 분류를 시킴으로써 어느정도 정렬이 된다. 이 이후에 Recursion을 통해서 pivot 기준 왼쪽/오른쪽 subarray를 정렬함으로써 최종적인 정렬이 완료된다

 

Pivot "Partition" 방식

어떤 pivot을 고르냐에 따라서 QuickSort의 시간복잡도가 결정된다

생각을 해보면 ASC | DESC로 정렬된 배열에서 QuickSort를 수행할 때 가장 최적의 pivot은 어느것일까?

>> 중앙에 있는 pivot을 고르는게 가장 normal하고 무난한 pivot이 될것이다

• 사실 "Good Pivot"은 "Median-Of-Medians"로 구할수는 있지만 여기서는 단순하게 배열의 중앙값으로 설정

 

1) left = 0 & right = list.length - 1 >> pivotPosition = (0 + 7) / 2 = 3

이제 4를 기준으로 4보다 작은 값들은 왼쪽 & 4보다 큰 값들은 오른쪽으로 분류하면 된다

 

 

2) Partition

1. c = -1 & i = 0

여기서 c가 의미하는 것은 "최종적인 pivot의 위치"이고, i는 배열의 index이다. 그리고 c는 partition 함수의 매개변수인 "left"에서 1을 뺀 값으로 처음 초기화를 해준다

i가 가리키고 있는 값인 5는 pivot인 4보다 크기 때문에 이 단계는 pass한다

 

2. c = -1 & i = 1

i가 가리키고 있는 값인 2는 pivot인 4보다 작기 때문에 c를 1 증가시켜주고 ( :: c = 0) c의 값과 i가 가리키는 값을 Swap해준다

 

3. c = 0 & i = 2

i가 가리키고 있는 값인 1인 pivot인 4보다 작기 때문에 c를 1 증가시켜주고 ( :: c = 1) c의 값과 i가 가리키는 값을 Swap해준다

 

 

4. c = 1 & i = 3

...

...

쭉 진행되다가 i가 가리키는 값이 3일 경우가 나타날 것이다

 

5. c = 1 & i = 6

i가 가리키는 값인 3은 pivot인 4보다 작기 때문에 c를 1 증가시켜주고 ( :: c = 2) c와 i의 값들을 Swap해준다

 

---

여기서 배열을 보게되면 pivot : 4를 기준으로 왼쪽에는 작은 값 & 오른쪽에는 큰 값들이 잘 분류가 되었다

 

>> 여기서 더이상 생각하지말고 Recursion으로 던져버리면 된다

그러면 Recursion 내에서 또 pivot을 찾고 Partition하고, 또 pivot을 찾고 Partition하고,.....를 반복함으로써 정렬이 알아서 된다

---

Java Code

static void QuickSort(int [] list, int left, int right){
    if(left < right) {
        int pivot = Partition(list, left, right);
        QuickSort(list, left, pivot - 1);
        QuickSort(list, pivot + 1, right);
    }
}

static int Partition(int [] list, int left, int right){
    int count = left - 1;
    /*
    count 변수는 "pivot"의 최종적인 위치를 결정해주는 변수이다
    >> 'count + 1'이 pivot의 최종 위치
     */
    int pivot = list[(left + right) / 2];
    // 중앙값으로 설정해주면 ASC/DESC 배열에서 QuickSort를 해도 최적으로 sort가 가능하다

    swap(list, right, (left + right) / 2); // 이를 통해서 pivot을 array의 가장 오른쪽으로 보내버린다

    for (int i = left; i < right; i++) {
        if (list[i] < pivot) {
            count += 1;
            swap(list, count, i);
        }
    }

    swap(list, right, (count + 1));

    return count + 1;
}

static void swap(int [] list, int a, int b){
    int tmp = list[a];
    list[a] = list[b];
    list[b] = tmp;
}

 

시간복잡도 분석

static int Partition(int [] list, int left, int right){
    int count = left - 1;

    int pivot = list[(left + right) / 2];

    swap(list, right, (left + right) / 2);

    for (int i = left; i < right; i++) {
        if (list[i] < pivot) {
            count += 1;
            swap(list, count, i);
        }
    }

    swap(list, right, (count + 1));

    return count + 1;
}

일단 Partition함수의 시간 복잡도는 O(n)이다

 

static void QuickSort(int [] list, int left, int right){
    if(left < right) {
        int pivot = Partition(list, left, right);
        QuickSort(list, left, pivot - 1);
        QuickSort(list, pivot + 1, right);
    }
}

QuickSort(int [] list, int left, int right)의 연산 수행 횟수를 T(n)이라고 하면 (n은 list의 길이)

결국 "pivot의 위치"에 따라서 시간복잡도가 결정된다

 

최악 : "pivot = 1" or "pivot = n"

- 최악의 경우 시간복잡도는 O(n²)이 된다

 

평균/최선 : "pivot = n/2"

- 이 경우 시간복잡도는 O(n log n)이 된다

 

---

Full Code (Java)

package Week_3;

public class Quick_Sort {
    static int tmp;
    public static void main(String[] args) {
        int [] list = {5, 2, 1, 4, 6, 7, 3, 8};

        System.out.println("정렬 전 list []");
        for(int n : list){
            System.out.print(n + " ");
        }
        System.out.println();
        QuickSort(list, 0, list.length - 1);

        System.out.println("\n정렬 후 list []");
        for(int n : list){
            System.out.print(n + " ");
        }
    }

    static void QuickSort(int [] list, int left, int right){
        if(left < right) {
            int pivot = Partition(list, left, right);
            QuickSort(list, left, pivot - 1);
            QuickSort(list, pivot + 1, right);
        }
    }

    static int Partition(int [] list, int left, int right){
        int count = left - 1;
        /*
        count 변수는 "pivot"의 최종적인 위치를 결정해주는 변수이다
        >> 'count + 1'이 pivot의 최종 위치
         */
        int pivot = list[(left + right) / 2];
        // 중앙값으로 설정해주면 ASC/DESC 배열에서 QuickSort를 해도 최적으로 sort가 가능하다

        swap(list, right, (left + right) / 2); // 이를 통해서 pivot을 array의 가장 오른쪽으로 보내버린다

        for (int i = left; i < right; i++) {
            if (list[i] < pivot) {
                count += 1;
                swap(list, count, i);
            }
        }

        swap(list, right, (count + 1));

        return count + 1;
    }

    static void swap(int [] list, int a, int b){
        int tmp = list[a];
        list[a] = list[b];
        list[b] = tmp;
    }
}