2022. 2. 26. 15:46ㆍMajor`/컴퓨터 네트워크
라우팅 프로토콜
- 라우팅 알고리즘이 필요로하는 Network의 정보들을 모으는 역할
- Router끼리 해당 정보를 주고받기 위해 필요한 프로토콜
- RIP / OSPF / BGP
라우팅 알고리즘
- Source → Dest까지 Router의 Network를 통과할 때 최적의 경로를 결정하기 위해 사용되는 알고리즘
- "좋은 경로" == "최소 비용 경로"
라우팅 알고리즘 분류
(1) 중앙 집중형 VS 분산형
▶ 중앙 집중형
- 네트워크의 전체적인 정보(완전한 정보)를 가지고 Source → Dest 까지의 최소 비용 경로를 계산
- 각 Router가 네트워크 전체 정보(링크 비용)을 보유하고 있다
- Link-State Algorithm :: LS Algorithm ≫ 다익스트라 알고리즘
▶ 분산형
- 최소 비용 경로의 계산이 Router들에 의해 반복적이고 분산된 방식으로 수행된다
- 각 Router는 자신의 이웃의 정보(링크 비용)만 보유하고 있다
- 이걸 자신의 이웃끼리 서로 공유하면서 결과적으로 전체적인 정보(링크 비용)을 보유하게 된다
- Distance-Vector Algorithm :: DV Algorithm ≫ 벨만-포드 알고리즘
(2) 정적 VS 동적
▶ 정적 라우팅 알고리즘
- 경로가 매우 느리게 변경되는 경우
- 사람이 Router Forwarding Table으로 직접 수정한다
▶ 동적 라우팅 알고리즘
- Network의 Traffic이나 Bandwidth에 의해서 경로를 주기적으로 변경한다
- 토플로지/링크 비용 변경에 대해서 직접 응답한다
링크 상태 라우팅 알고리즘 (Link-State Algorithm :: 다익스트라 알고리즘)
- 각 Router는 전체 네트워크 상태에 대한 정보가 필요하고, Router끼리 자신이 알고있는 정보를 교환하려고 한다
- 정보를 교환하기 위한 패킷 : LSA (Link-State Advertisement)
- 현재 Link들의 연결 상태 (끊어짐/연결)
- 지연시간 or 현재 남아있는 용량
- Router가 생성한 LSA는 자신이 속한 Network에 있는 모든 Router들에게 전송된다
- 이렇게 LSA를 Router끼리 공유함으로써 전체 네트워크 상태를 구성할 수 있게 된다
다익스트라 알고리즘
- 기준 노드에서 각 최단 비용 경로 집합(N)을 넓히면서 결과적으로 모든 Router가 네트워크 상태를 알게 된다
Example)
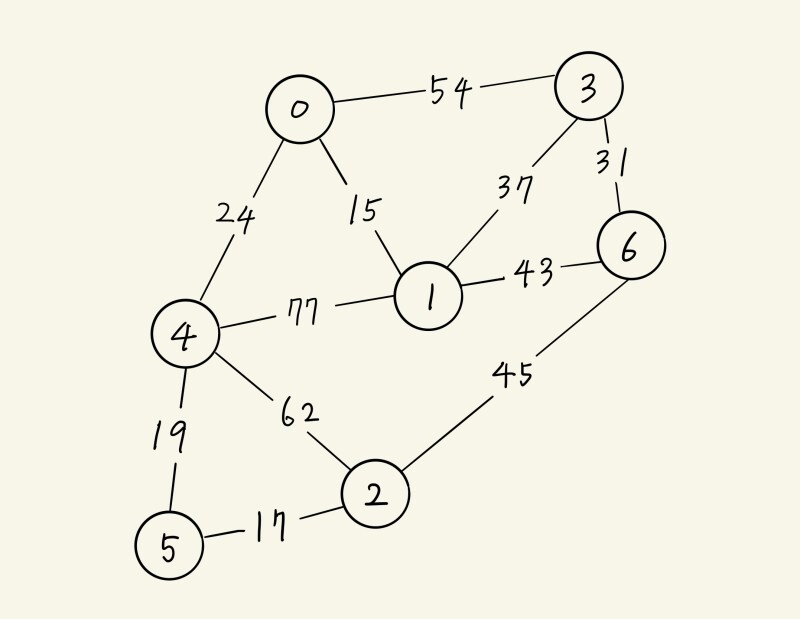
- 0에서부터 시작 & 0 ~ 모든 정점까지의 비용 초기화 (연결되어 있지 않으면 INF로 초기화)
| D(1) | D(2) | D(3) | D(4) | D(5) | D(6) |
| V(0) & 15 | ∞ | V(0) & 54 | V(0) & 24 | ∞ | ∞ |
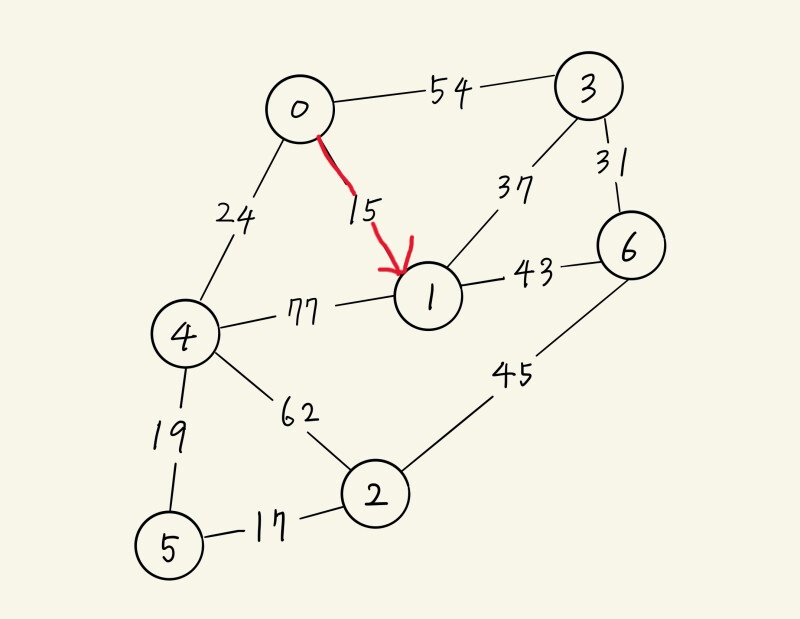
| D(1) | D(2) | D(3) | D(4) | D(5) | D(6) |
| V(0) & 15 | ∞ | V(0) & 54 | V(0) & 24 | ∞ | ∞ |
| <경로> 0 → 1 |
∞ | V(1) & 52 | V(0) & 24 | ∞ | V(1) & 58 |
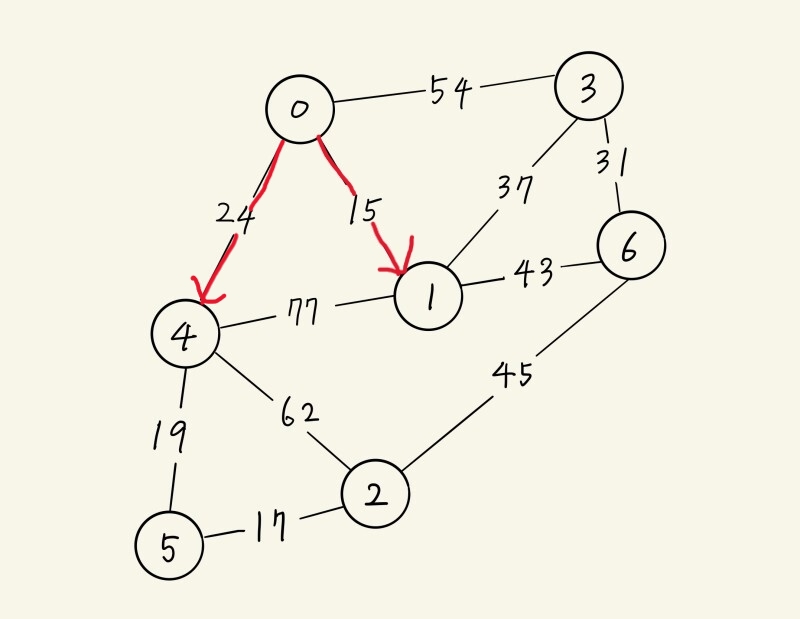
| D(1) | D(2) | D(3) | D(4) | D(5) | D(6) |
| V(0) & 15 | ∞ | V(0) & 54 | V(0) & 24 | ∞ | ∞ |
| <경로> 0 → 1 |
∞ | V(1) & 52 | V(0) & 24 | ∞ | V(1) & 58 |
| <경로> 0 → 1 |
∞ | V(1) & 52 | <경로> 0 → 4 |
V(4) & 43 | V(1) & 58 |

| D(1) | D(2) | D(3) | D(4) | D(5) | D(6) |
| V(0) & 15 | ∞ | V(0) & 54 | V(0) & 24 | ∞ | ∞ |
| <경로> 0 → 1 |
∞ | V(1) & 52 | V(0) & 24 | ∞ | V(1) & 58 |
| <경로> 0 → 1 |
∞ | V(1) & 52 | <경로> 0 → 4 |
V(4) & 43 | V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | V(1) & 52 | <경로> 0 → 4 |
<경로> 0 → 4 → 5 |
V(1) & 58 |
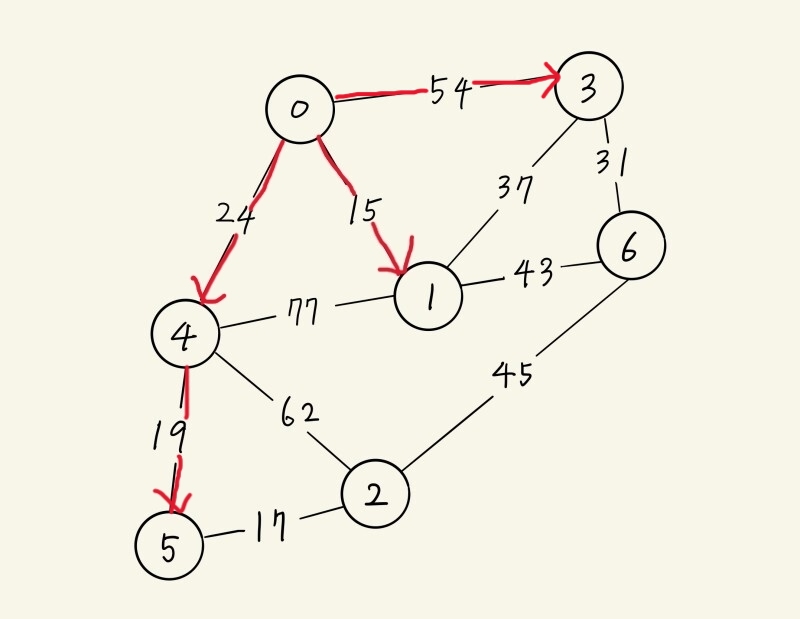
| D(1) | D(2) | D(3) | D(4) | D(5) | D(6) |
| V(0) & 15 | ∞ | V(0) & 54 | V(0) & 24 | ∞ | ∞ |
| <경로> 0 → 1 |
∞ | V(1) & 52 | V(0) & 24 | ∞ | V(1) & 58 |
| <경로> 0 → 1 |
∞ | V(1) & 52 | <경로> 0 → 4 |
V(4) & 43 | V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | V(1) & 52 | <경로> 0 → 4 |
<경로> 0 → 4 → 5 |
V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | <경로> 0 → 1 → 3 |
<경로> 0 → 4 |
<경로> 0 → 4 → 5 |
V(1) & 58 |
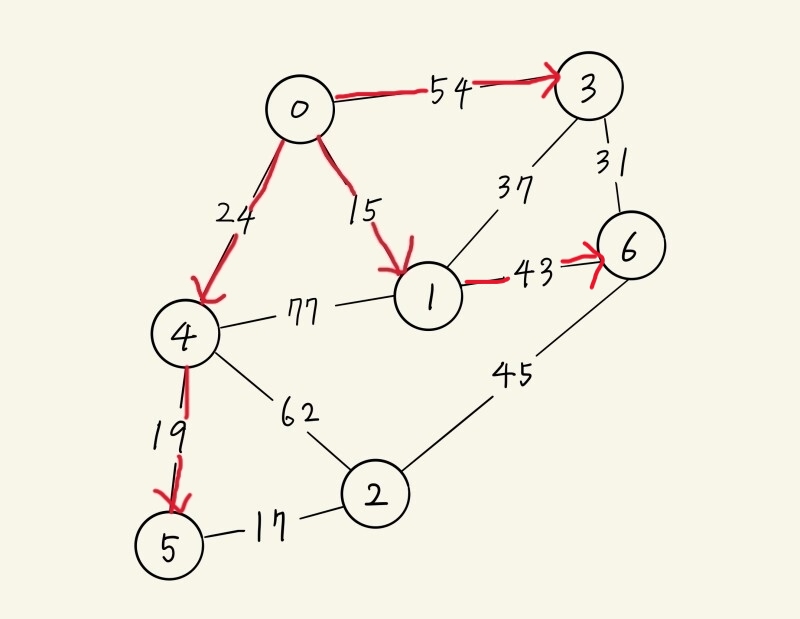
| D(1) | D(2) | D(3) | D(4) | D(5) | D(6) |
| V(0) & 15 | ∞ | V(0) & 54 | V(0) & 24 | ∞ | ∞ |
| <경로> 0 → 1 |
∞ | V(1) & 52 | V(0) & 24 | ∞ | V(1) & 58 |
| <경로> 0 → 1 |
∞ | V(1) & 52 | <경로> 0 → 4 |
V(4) & 43 | V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | V(1) & 52 | <경로> 0 → 4 |
<경로> 0 → 4 → 5 |
V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | <경로> 0 → 1 → 3 |
<경로> 0 → 4 |
<경로> 0 → 4 → 5 |
V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | <경로> 0 → 1 → 3 |
<경로> 0 → 4 |
<경로> 0 → 4 → 5 |
<경로> 0 → 1 → 6 |
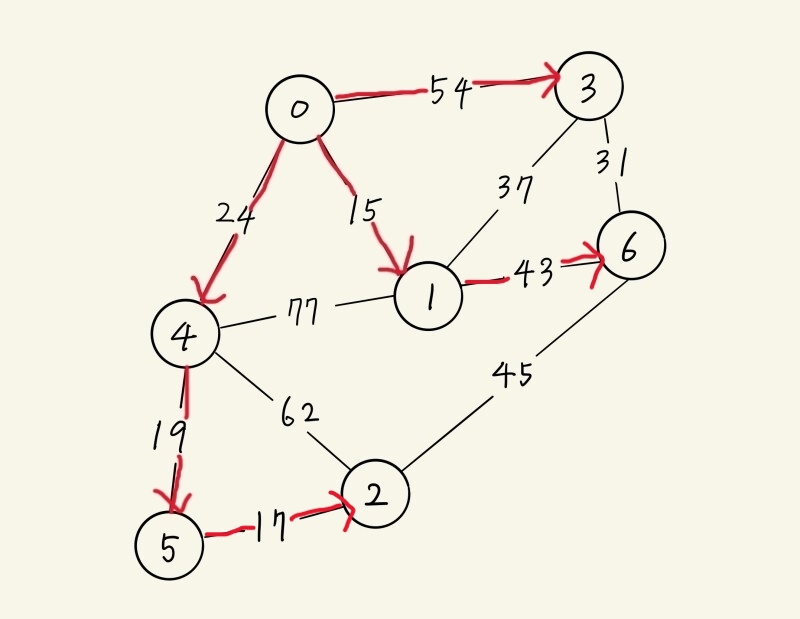
| D(1) | D(2) | D(3) | D(4) | D(5) | D(6) |
| V(0) & 15 | ∞ | V(0) & 54 | V(0) & 24 | ∞ | ∞ |
| <경로> 0 → 1 |
∞ | V(1) & 52 | V(0) & 24 | ∞ | V(1) & 58 |
| <경로> 0 → 1 |
∞ | V(1) & 52 | <경로> 0 → 4 |
V(4) & 43 | V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | V(1) & 52 | <경로> 0 → 4 |
<경로> 0 → 4 → 5 |
V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | <경로> 0 → 1 → 3 |
<경로> 0 → 4 |
<경로> 0 → 4 → 5 |
V(1) & 58 |
| <경로> 0 → 1 |
V(5) & 60 | <경로> 0 → 1 → 3 |
<경로> 0 → 4 |
<경로> 0 → 4 → 5 |
<경로> 0 → 1 → 6 |
| <경로> 0 → 1 |
<경로> 0 → 4 → 5 → 2 |
<경로> 0 → 1 → 3 |
<경로> 0 → 4 |
<경로> 0 → 4 → 5 |
<경로> 0 → 1 → 6 |
| 최종 경로 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| <경로> 0 → 4 → 5 |
<경로> 0 → 4 → 5 → 2 |
<경로> 0 → 1 → 3 |
<경로> 0 → 4 |
<경로> 0 → 4 → 5 |
<경로> 0 → 1 → 6 |
거리 벡터 알고리즘 (Distance-Vector Algorithm :: 벨만-포드 알고리즘)
- 이웃하는 노드의 거리-벡터만 아는 상황에서 최소 거리를 구한다
- 각 Router는 자신과 이웃한 Router까지의 거리-벡터만 아는 상태이다
- 여기서 서로 이웃끼리 자신이 아는 거리-벡터를 공유함으로써 점점 퍼져나간다
- 다 퍼져나가면 결국 모든 Router는 이웃끼리의 거리-벡터 테이블을 동일하게 보유하고있다

- x ~ y의 경로
- v : x의 이웃 Router
Example)
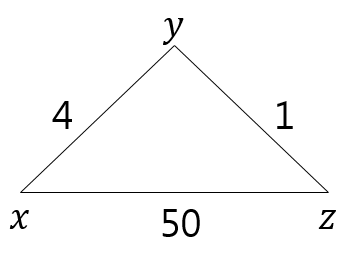
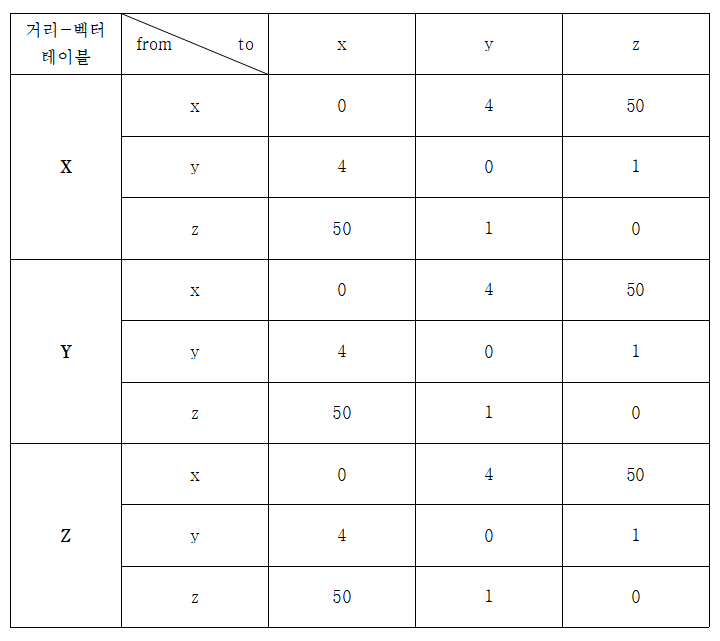
# 초기 x, y, z의 거리-벡터 테이블
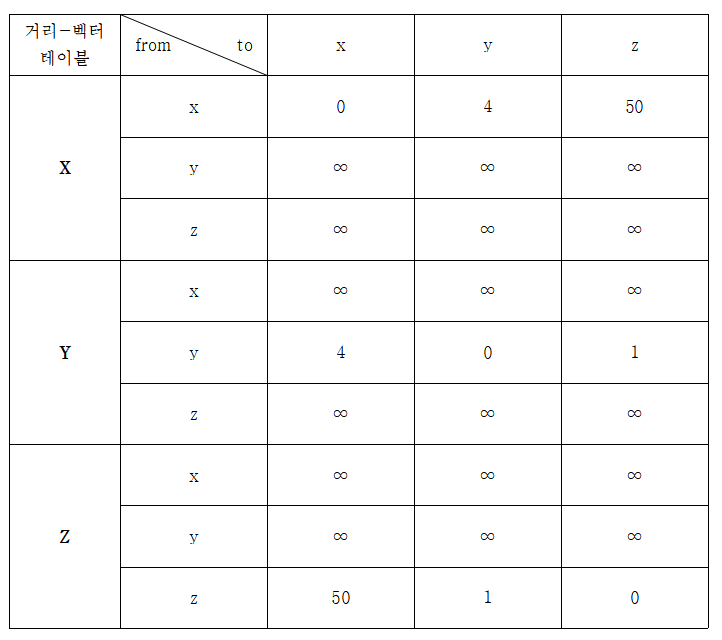
1. 서로서로 자신이 알고있는 거리-벡터들을 공유한다
- X(0, 4, 50) → Y, Z
- Y(4, 0, 1) → X, Z
- Z(50, 1, 0) → X, Y
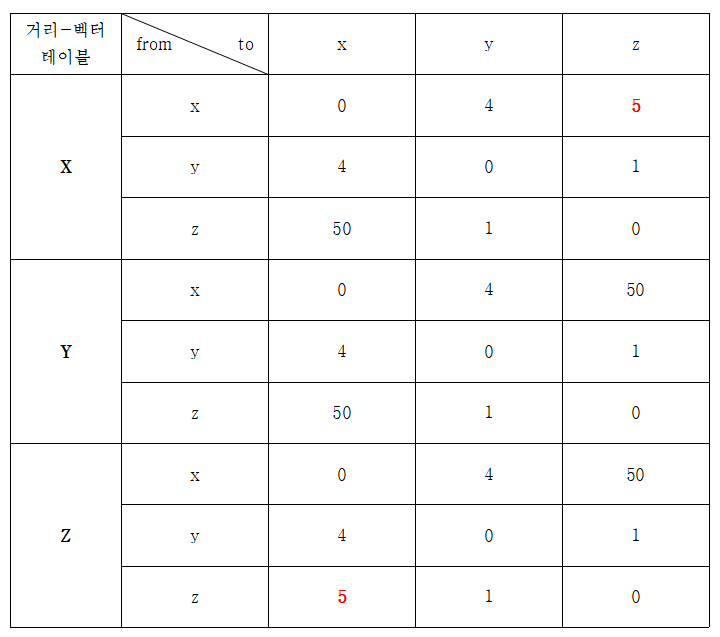
2. 이웃으로부터 새로운 DV를 받았으므로 각자 자신의 거리-벡터 테이블을 업데이트해야 한다
DX(Z)
- Min(x~y + y~z & x~z + z~z)
- Min(4+1 & 50+0)
- >> 5
DZ(X)
- Min(z~y + y~x & z~x + x~x)
- Min(1+4 & 50+0)
- >> 5
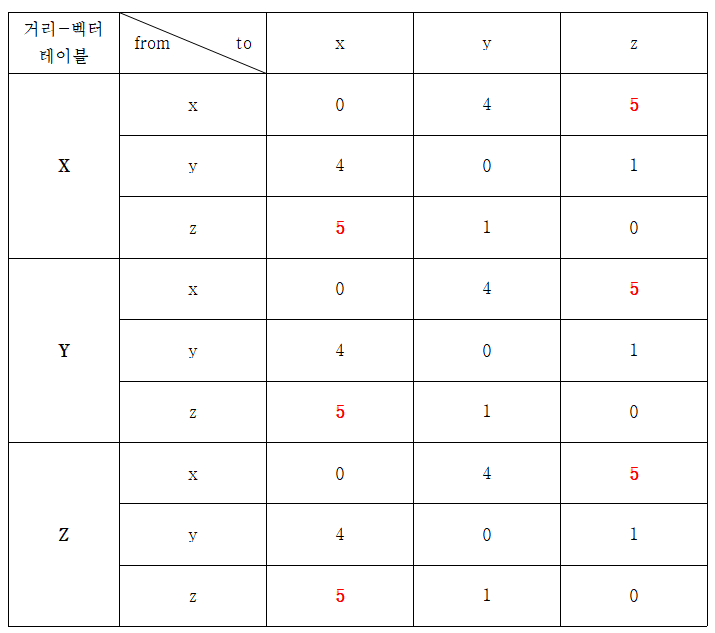
3. X, Y는 자신의 거리-벡터 테이블정보가 변경되었으니까 각자 이웃 Router에게 변경된 내용을 알려야 한다
링크 비용 변경 :: 라우팅 루프
1) 비용이 감소
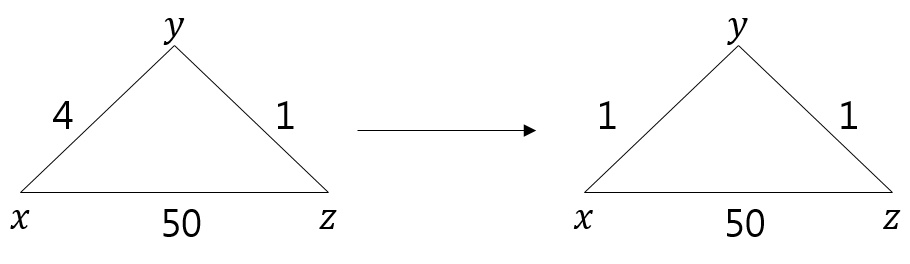
- 링크 비용이 감소하는 "좋은 소식"의 경우 네트워크 전역에 빨리 전파를 한다
2) 비용이 증가
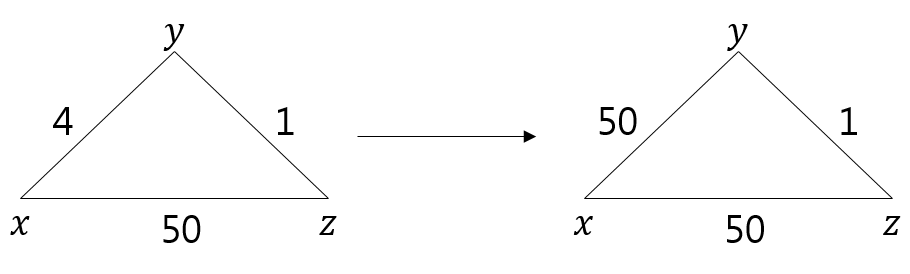
- 링크 비용이 증가하는 "나쁜 소식"의 경우 네트워크 전역에 느리게 전파를 한다
- 이 때, 라우팅 루프가 발생한다 :: 무한 카운트 (Count To Infiinity)
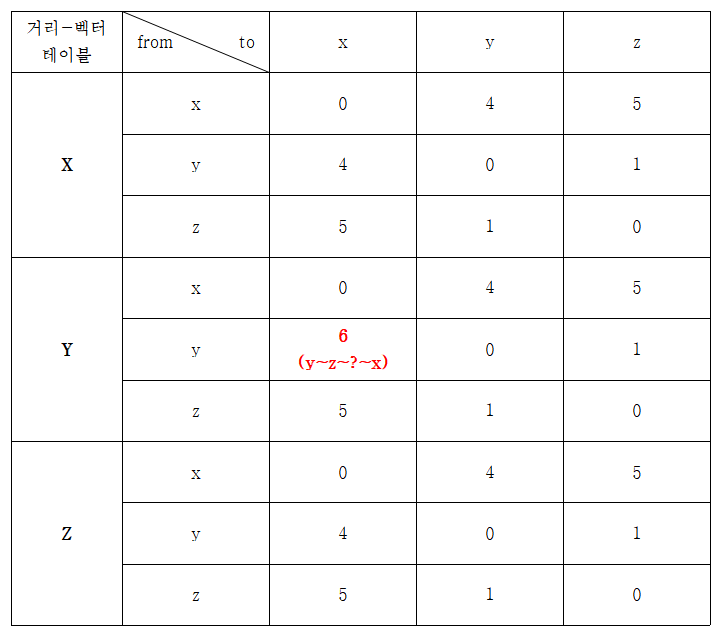
Y가 X로가는 링크의 비용 변경을 감지하고 자신의 거리-벡터 테이블을 변경할 때
- DY(X) = Min(y~x + x~x & y~z + z~x) = Min(60+0 & 1+5) = 6
- DZ(X)는 4~60으로 변경 시, 50이 되는데 Y에서 먼저 거리-벡터 테이블을 변경하기 때문에 이 변화가 적용되지 않고 원래 DZ(X)의 값 : 5로 계산이 된다
- 이러면 DZ(X)가 7 ~ DY(X)가 다시 8 ~ DZ(X)가 다시 9 ~~ 이렇게 루프를 돌게 된다
- 이렇게 계속해서 라우팅 루프가 발생하게 되면서 최소 44번 반복해야 경로 비용이 50보다 크다는 사실을 알 수 있게 된다
무한 루프 해결 방법 : 포이즌 리버스 (Poisoned Reverse)
- 결국 z ~ x로 갈 때 y에 의존해서 비용을 계산하므로 이런 문제가 발생한다
- 해결 방안은 z ~ y ~ x의 경로일 때, z는 y에게 DZ(X)가 무한대라고 알려주면 해결이 된다
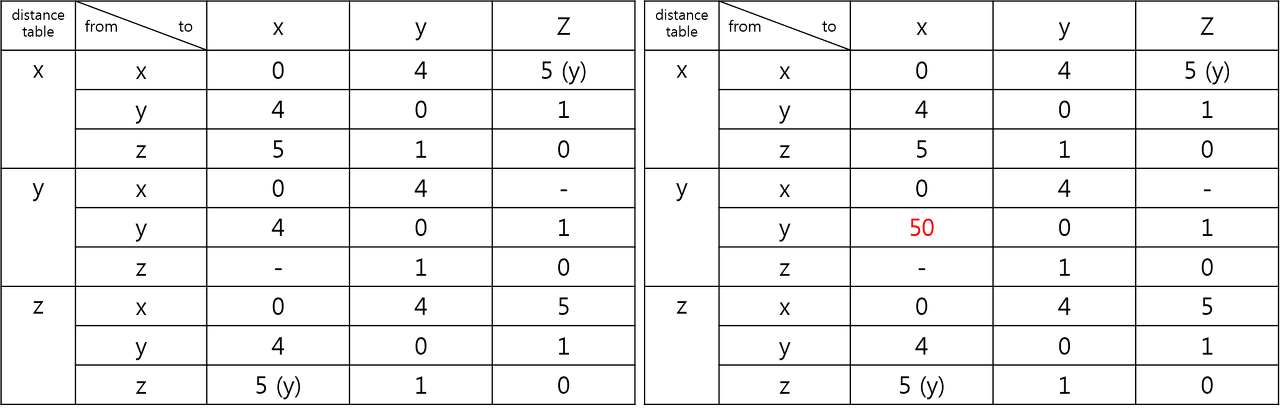
- 물론 이 해결방안은 2개의 이웃 노드에 대해서 루프가 발생할 경우이다
- 3개 이상의 이웃 노드에 대해서 루프가 발생하면 감지를 하지 못한다
