[Data Structure] 합병 정렬 - Merge Sort

합병 정렬 (Merge Sort)

Stable Sort

• 분할 정복(Divide and Conquer) 기법 (순환 호출로 구현)

1. 하나의 리스트를 2개의 균등한 크기로 분할 

2. 분할된 부분 리스트들을 각각 정렬 

3. 최종 정렬된 2개의 부분 리스트를 합해서 하나의 정렬된 리스트로 생성

• 추가적인 리스트가 필요하다
• 각 부분 리스트를 정렬할 때, 합병 정렬을 순환 호출해서 정렬
• 실제로 정렬이 이루어지는 시점은 최종적으로 정렬된 2개의 부분 리스트를 합병하는 단계(3)이다
• Java의 Collections.sort는 합병정렬로 구현

 

시간복잡도

- O(n log n)

 

장점

- 항상 O(n log n)이라는 시간복잡도를 가진다

 

단점

- 추가적인 메모리가 필요하다

- 추가 메모리를 할당할 수 없으면 Quick Sort를 사용한다

 

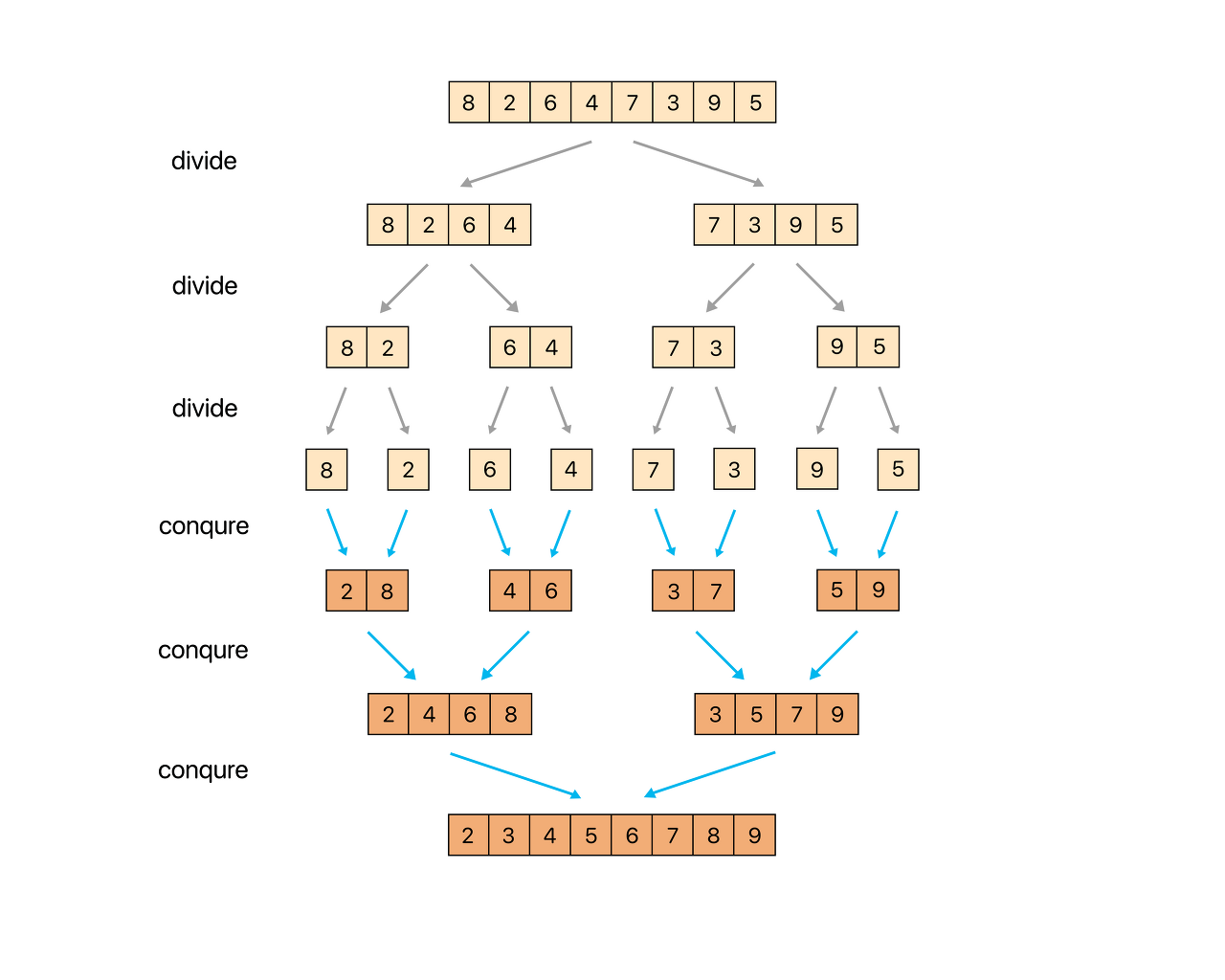
과정

1. 분할(Divide) : 정렬할 배열을 같은 크기의 2개의 부분 배열로 분할 (merge_sort)
2. 정복(Conquer) : 부분 배열들을 각각 정렬 / 부분 배열의 길이가 1이 아니면 Divide 순환 호출
3. 결합(Combine) : 최종 정렬된 2개의 부분 배열을 하나의 정렬된 배열로 통합 (merge)

 

 

Merge Sort Code

static void merge_sort(int A[], int left, int right){
        if (left == right) return;
        // left와 right가 같다는 것은 부분 리스트의 길이가 1
        // 부분 리스트의 길이가 1이면 더이상 분할 X
        int mid = (left+right)/2;
        merge_sort(A, left, mid); // 2등분 한 front 리스트 정렬 (길이 1 될 때 까지)
        merge_sort(A, mid+1, right); // 2등분 한 back 리스트 정렬 (길이 1 될 때 까지)
        merge(A, left, mid, right); // 길이가 1인 각각의 부분 리스트들을 merge
    }

    static void merge(int A[], int left, int mid, int right){
        int l = left;
        int r = mid+1;
        int index = left;


        while(l<=mid && r<=right){
            // front 리스트(l), back 리스트(r)
            if(A[l] < A[r]) {
                // back 리스트의 값이 더 크면
                sorted[index++] = A[l++];
                // 값이 작은 front 리스트의 요소를 sorted 배열에 추가
            }
            else {
                // front 리스트의 값이 더 크면
                sorted[index++] = A[r++];
                // 값이 작은 back 리스트의 요소를 sorted 배열에 추가
            }
        }
        if(l>mid){
            // front 리스트의 요소들을 전부 sorted 배열에 추가했으면
            while(r<=right)
                // back 리스트의 남은 요소들을 차례대로 sorted 배열에 추가
                sorted[index++] = A[r++];
        }
        else{
            // back 리스트의 요소들을 전부 sorted 배열에 추가했으면
            while(l<=mid)
                // front 리스트의 남은 요소들을 차례대로 sorted 배열에 추가
                sorted[index++] = A[l++];
        }
        for(int i=left; i<=right; i++)
            // sorted 배열은 임시 배열이니까 원래 정렬할 배열에 copy
            A[i] = sorted[i];
    }

 

 

Full Code

package Sort;

import java.util.Calendar;

public class Merge_Sort_5 {
    private static int[] sorted = new int[8]; // sorted 임시 배열 (부분 리스트)
    static int conqure = 1;
    public static void main(String[] args) {
        int [] A = {8, 2, 6, 4, 7, 3, 9, 5}; // 정렬할 배열 A

        // 정렬 전 A 출력
        System.out.print("A[]");
        for(int i=0; i<A.length; i++){
            if(i%20==0) System.out.println();
            System.out.print(A[i] + "\t");
        }
        System.out.println("\n");

        Calendar before = Calendar.getInstance();
        merge_sort(A, 0, A.length-1);
        Calendar after = Calendar.getInstance();
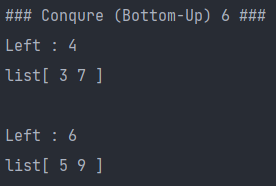
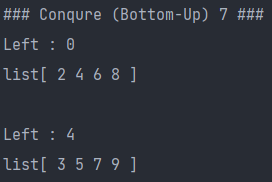
        System.out.println("### Conqure (Bottom-Up) " + (conqure++) +" ###");

        //conqure 단계 표시 (왼쪽 -> 오른쪽)
        System.out.print("Left : "+ "0" + "\nlist[ ");
        for(int i=0; i<sorted.length; i++) {
            System.out.print(sorted[i] + " ");
        }
        System.out.print("]\n\n");

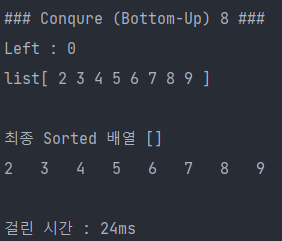
        System.out.print("최종 Sorted 배열 []");
        for(int i=0; i<sorted.length; i++){
            if(i%20==0) System.out.println();
            System.out.print(sorted[i] + "\t");
        }
        System.out.println("\n");

        int time = after.get(Calendar.MILLISECOND) - before.get(Calendar.MILLISECOND);
        System.out.println("걸린 시간 : " + time + "ms");
    }

    static void merge_sort(int A[], int left, int right){
        if (left == right) return;
        // left와 right가 같다는 것은 부분 리스트의 길이가 1
        // 부분 리스트의 길이가 1이면 더이상 분할 X
        int mid = (left+right)/2;
        merge_sort(A, left, mid); // 2등분 한 front 리스트 정렬 (길이 1 될 때 까지)
        merge_sort(A, mid+1, right); // 2등분 한 back 리스트 정렬 (길이 1 될 때 까지)
        System.out.println("### Conqure (Bottom-Up) " + (conqure++) +" ###");
        merge(A, left, mid, right); // 길이가 1인 각각의 부분 리스트들을 merge
    }

    static void merge(int A[], int left, int mid, int right){
        int l = left;
        int r = mid+1;
        int index = left;

        System.out.print("Left : "+ l + "\nlist[ ");
        for(int i=left; i<=mid; i++) {
            System.out.print(A[i] + " ");
        }
        System.out.print("]\n\n");
        System.out.print("Left : "+ r + "\nlist[ ");
        for(int i=mid+1; i<=right; i++) {
            System.out.print(A[i] + " ");
        }
        System.out.print("]\n\n");

        while(l<=mid && r<=right){
            // front 리스트(l), back 리스트(r)
            if(A[l] < A[r]) {
                // back 리스트의 값이 더 크면
                sorted[index++] = A[l++];
                // 값이 작은 front 리스트의 요소를 sorted 배열에 추가
            }
            else {
                // front 리스트의 값이 더 크면
                sorted[index++] = A[r++];
                // 값이 작은 back 리스트의 요소를 sorted 배열에 추가
            }
        }
        if(l>mid){
            // front 리스트의 요소들을 전부 sorted 배열에 추가했으면
            while(r<=right)
                // back 리스트의 남은 요소들을 차례대로 sorted 배열에 추가
                sorted[index++] = A[r++];
        }
        else{
            // back 리스트의 요소들을 전부 sorted 배열에 추가했으면
            while(l<=mid)
                // front 리스트의 남은 요소들을 차례대로 sorted 배열에 추가
                sorted[index++] = A[l++];
        }
        for(int i=left; i<=right; i++)
            // sorted 배열은 임시 배열이니까 원래 정렬할 배열에 copy
            A[i] = sorted[i];
    }
}

▶ 부분 리스트 길이가 1이 될 때 까지 분할한 후, Conqure (왼쪽 서브트리) -- (1)

▶ 부분 리스트 길이가 1이 될 때 까지 분할한 후, Conqure (오른쪽 서브트리) -- (1)

▶ (1)에서 Conqure한 각각의 부분 리스트들을 또 Conqure