2021. 12. 24. 19:51ㆍMajor`/자료구조
신장 트리 (Spanning Tree)
- 그래프의 모든 정점들을 포함하는 트리
- 모든 정점들이 연결되어 있어야 하고, 사이클을 포함하면 안된다
최소 신장 트리 (Minimum Spanning Tree)
- 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 신장트리
- 모든 정점들을 가장 적은 수의 간선, 비용으로 연결
- n개의 정점들에 대해 반드시 n-1개의 간선만 사용 + 사이클 포함 X
- ex) 도로 건설, 전기 회로, 통신, 배관,....
Kruskal Algorithm, Prim Algorithm
Kruskal MST Algorithm
- 탐욕적 방법 (greedy method) 이용
- 간선을 기반으로 하는 알고리즘
- 간선의 개수 e개 → O(|e|log₂|e|)
- 매 선택마다 최선의 선택을 수행 → 반복하면서 최종적 해답에 도달
- 이 최종적 해답이 전역적으로 최적이라는 보장은 없다
- 증명 방법 : 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택
- 간선(edge)들의 가중치를 오름차순(ASC)으로 정렬
- 사이클 형성하지 않는 간선을 찾아서 현재 MST 집합에 추가
- 사이클 형성하면 해당 간선은 pass하고 오름차순으로 정렬된 집합에서 해당 간선의 다음 간선을 선택
- 간선의 개수가 그래프의 정점 개수보다 1개 적어지면 알고리즘 종료
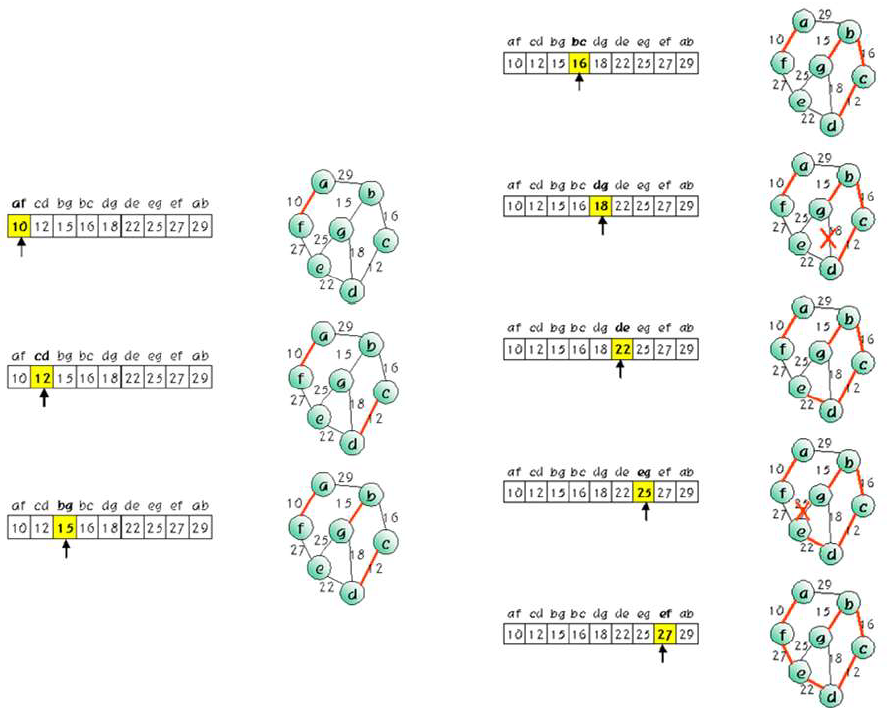
사이클 체크
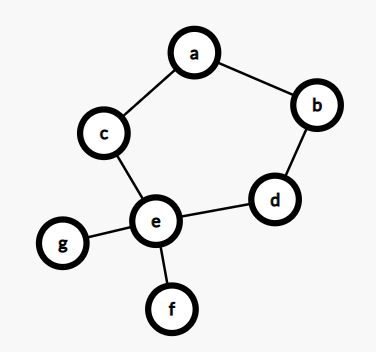

(1)에서의 집합 (a, b)
- {a, b, c, d, e}
- a, b가 같은 집합에 포함되어 있다
- 사이클 형성 (간선의 양끝 정점이 같은 집합에 포함)
(2)에서의 집합 (a, b)
- {b, c, d}, a
- a, b가 서로 다른 집합에 속한다
- → 사이클 형성 X
사이클 검사 알고리즘 → union-find Algorithm
union-find Algorithm
- union(x, y) : 원래 집합에서 x, y를 묶은 합집합을 생성
- find(x) : x가 속해있는 집합 return
ex) S = {1, 2, 3, 4, 5, 6}
- union(1, 4), union(5, 2) → {1, 4}, {5, 2}, {3}, {6}
- union(4, 5) union(3, 6) → {1, 4, 5, 2}, {3, 6}
union-find 구현
- 가장 효율적인 트리 형태 사용
- 부모 노드만 알면 되기 때문에 '부모 포인터 표현'를 사용
- 부모 포인터 표현 → 1차원 배열로 구현
if 원소 a, b의 최종부모노드가 동일 → a, b를 연결하면 사이클 발생
※ Example

- 정점 = 7개
- 선택된 간선이 정점-1개, 즉 6개면 즉시 알고리즘 종료
- 칸 숫자 1씩 마이너스 시키고 예제
- edge별 가중치 표 (무방향)
| start | end | weight(가중치) |
| 1 | 2 | 5 |
| 1 | 3 | 10 |
| 2 | 3 | 7 |
| 2 | 4 | 6 |
| 2 | 5 | 9 |
| 3 | 4 | 12 |
| 3 | 6 | 2 |
| 4 | 6 | 11 |
| 4 | 7 | 15 |
| 5 | 7 | 3 |
| 6 | 7 | 14 |
▶ 각 정점의 최종 부모노드 (처음에는 각 정점의 번호로 초기화)
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 최종 부모 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1. 가중치 오름차순으로 정렬 (qsort())
| start | end | weight(가중치) |
| 3 | 6 | 2 |
| 5 | 7 | 3 |
| 1 | 2 | 5 |
| 2 | 4 | 6 |
| 2 | 3 | 7 |
| 2 | 5 | 9 |
| 1 | 3 | 10 |
| 4 | 6 | 11 |
| 3 | 4 | 12 |
| 6 | 7 | 14 |
| 4 | 7 | 15 |
2. 가중치가 적은 순서대로 (start, end) 선택 + 사이클 발생 X
- start와 end의 최종부모가 다르면, parent[end] = start로 설정 후, 계속 진행
- start와 end의 최종부모가 같으면 사이클 발생 → 해당 (start, end)는 pass
최종부모 파악
- → parent[curr] == curr이면 curr의 최종부모는 그대로 curr
- → parent[curr] != curr이면, curr = parent[curr]을 계속 대입해서 최종 부모 파악
▶ (3, 6) : 3의 최종부모 = 3 / 6의 최종부모 = 6 (O)
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 최종 부모 정점 | 1 | 2 | 3 | 4 | 5 | 3 | 7 |
▶ (5, 7) : 5의 최종부모 = 5 / 7의 최종부모 = 7 (O)
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 최종 부모 정점 | 1 | 2 | 3 | 4 | 5 | 3 | 5 |
▶ (1, 2) : 1의 최종부모 = 1 / 2의 최종부모 = 2 (O)
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 최종 부모 정점 | 1 | 1 | 3 | 4 | 5 | 3 | 5 |
▶ (2, 4) : 2의 최종부모 = 1 / 4의 최종부모 = 4 (O)
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 최종 부모 정점 | 1 | 1 | 3 | 1 | 5 | 3 | 5 |
▶ (2, 3) : 2의 최종부모 = 1 / 3의 최종부모 = 3 (O)
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 최종 부모 정점 | 1 | 1 | 1 | 1 | 5 | 3 | 5 |
▶ (2, 5) : 2의 최종부모 = 1 / 5의 최종부모 = 5 (O)
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 최종 부모 정점 | 1 | 1 | 1 | 1 | 1 | 3 | 5 |
- 지금 단계까지 선택된 간선이 6개이므로, 알고리즘 즉시 종료
- (3, 6) → (5, 7) → (1, 2) → (2, 4) → (2, 3) → (2, 5) / 총 가중치 = 2+3+5+6+7+9 = 32
▶ Graph Code
// 그래프 구현
typedef struct {
int start, end;
int weight; // 가중치
}edge;
typedef struct graph {
int n; // 간선 개수
edge edges[2 * MAX_VERTEX]; // vertex 1개당 edge = 2개(무방향)
}graph;
graph* create() {
return (graph*)malloc(sizeof(graph));
}
void init_graph(graph* g) {
g->n = 0;
for (int i = 0; i < 2 * MAX_VERTEX; i++) {
g->edges[i].start = 0;
g->edges[i].end = 0;
g->edges[i].weight = 0;
}
}
void insert_edge(graph* g, int start, int end, int weight) {
g->edges[g->n].start = start;
g->edges[g->n].end = end;
g->edges[g->n].weight = weight;
g->n++;
}
▶ Union-Find Algorithm Code
// union-find algorithm
int parent[MAX_VERTEX];
void init_parent() {
// 모든 vertex의 parent를 각 vertex 번호로 초기화
for (int i = 0; i <MAX_VERTEX; i++)
parent[i] = i;
}
int find_parent(int curr) {
if (parent[curr] == curr)
return curr;
else
return find_parent(parent[curr]);
// 최종 부모 정점을 recursive를 통해서 return
}
void set_parent(int start, int end){
start = find_parent(start);
end = find_parent(end);
if (start > end)
parent[start] = end;
else
parent[end] = start;
}
▶ Kruskal Algorithm Code
void kruskal_mst(graph* g, int v) {
// v = 정점의 개수 (개발자가 직접 insert)
int edge_count = 0; // 선택한 간선의 수가 정점-1개, 즉 v-1개이면 알고리즘 종료
int start, end;
edge e;
init_parent();
qsort(g->edges, g->n, sizeof(edge), compare);
printf("Kruskal MST Algorithm\n");
int i = 0;
int cost = 0; // 각 단계마다 누적되는 비용
while (edge_count < v - 1) {
// Kruskal Algorithm에서 edge의 개수는 vertex의 개수보다 반드시 1개 적어야 한다
e = g->edges[i];
start = find_parent(e.start);
end = find_parent(e.end);
if (start != end) {
// 최종 부모가 다르면 사이클이 발생하지 않기 때문에 최종 부모가 다른경우에만 실행
cost += e.weight;
printf("Edge : (%d, %d) Weight : %d 선택 -> 현재 비용 : %d\n", e.start, e.end, e.weight, cost);
edge_count++;
set_parent(start, end);
}
else {
// 최종 부모가 같으면 사이클이 발생
printf("Edge : (%d, %d) Fail -> Cycle Occurrence\n", e.start, e.end);
}
i++;
}
printf("최종 비용 : %d\n", cost);
}
※ Example
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX 100
#define TRUE 1
#define FALSE 0
#define INF 1000
// union-find algorithm
int parent[MAX_VERTEX];
void init_parent() {
// 모든 vertex의 parent를 각 vertex 번호로 초기화
for (int i = 0; i <MAX_VERTEX; i++)
parent[i] = i;
}
int find_parent(int curr) {
if (parent[curr] == curr)
return curr;
else
return find_parent(parent[curr]);
// 최종 부모 정점을 recursive를 통해서 return
}
void set_parent(int start, int end){
start = find_parent(start);
end = find_parent(end);
if (start > end)
parent[start] = end;
else
parent[end] = start;
}
// 그래프 구현
typedef struct {
int start, end;
int weight; // 가중치
}edge;
typedef struct graph {
int n; // 간선 개수
edge edges[2 * MAX_VERTEX]; // vertex 1개당 edge = 2개(무방향)
}graph;
graph* create() {
return (graph*)malloc(sizeof(graph));
}
void init_graph(graph* g) {
g->n = 0;
for (int i = 0; i < 2 * MAX_VERTEX; i++) {
g->edges[i].start = 0;
g->edges[i].end = 0;
g->edges[i].weight = 0;
}
}
void insert_edge(graph* g, int start, int end, int weight) {
g->edges[g->n].start = start;
g->edges[g->n].end = end;
g->edges[g->n].weight = weight;
g->n++;
}
int compare(const void* a, const void* b) {
// 각 edge의 weight를 오름차순으로 비교 후 정렬
edge* x = (edge*)a;
edge* y = (edge*)b;
if (x->weight > y->weight)
return 1;
else if (x->weight < y->weight)
return -1;
else
return 0;
}
void kruskal_mst(graph* g, int v) {
// v = 정점의 개수 (개발자가 직접 insert)
int edge_count = 0; // 선택한 간선의 수가 정점-1개, 즉 v-1개이면 알고리즘 종료
int start, end;
edge e;
init_parent();
qsort(g->edges, g->n, sizeof(edge), compare);
printf("Kruskal MST Algorithm\n");
int i = 0;
int cost = 0; // 각 단계마다 누적되는 비용
while (edge_count < v - 1) {
// Kruskal Algorithm에서 edge의 개수는 vertex의 개수보다 반드시 1개 적어야 한다
e = g->edges[i];
start = find_parent(e.start);
end = find_parent(e.end);
if (start != end) {
// 최종 부모가 다르면 사이클이 발생하지 않기 때문에 최종 부모가 다른경우에만 실행
cost += e.weight;
printf("Edge : (%d, %d) Weight : %d 선택 -> 현재 비용 : %d\n", e.start, e.end, e.weight, cost);
edge_count++;
set_parent(start, end);
}
else {
// 최종 부모가 같으면 사이클이 발생
printf("Edge : (%d, %d) Fail -> Cycle Occurrence\n", e.start, e.end);
}
i++;
}
printf("최종 비용 : %d\n", cost);
}
int main(void) {
graph* g, *g1;
g = create(); init_graph(g);
g1 = create(); init_graph(g1);
insert_edge(g, 1, 2, 5);
insert_edge(g, 1, 3, 10);
insert_edge(g, 2, 3, 7);
insert_edge(g, 2, 4, 6);
insert_edge(g, 2, 5, 9);
insert_edge(g, 3, 4, 12);
insert_edge(g, 3, 6, 2);
insert_edge(g, 4, 6, 11);
insert_edge(g, 4, 7, 15);
insert_edge(g, 5, 7, 3);
insert_edge(g, 6, 7, 14);
printf("----------------------------------------------------\n");
kruskal_mst(g, 7);
printf("----------------------------------------------------\n");
free(g);
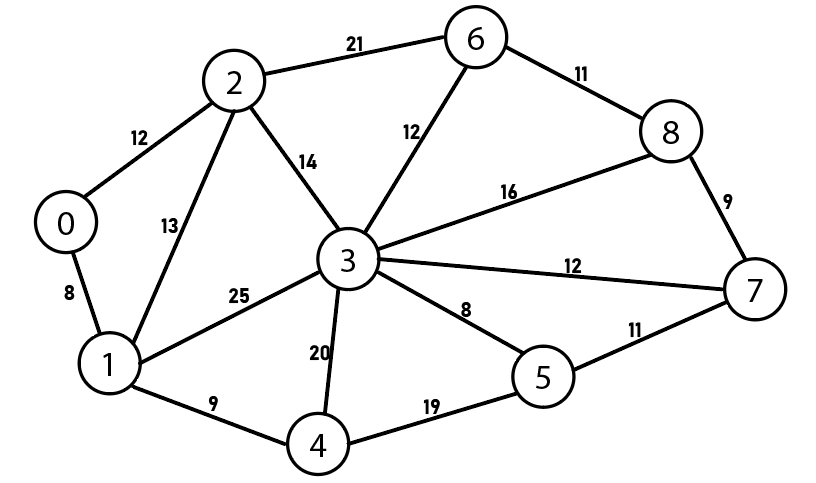
insert_edge(g1, 0, 1, 8);
insert_edge(g1, 0, 2, 12);
insert_edge(g1, 1, 2, 13);
insert_edge(g1, 1, 3, 25);
insert_edge(g1, 1, 4, 9);
insert_edge(g1, 2, 3, 14);
insert_edge(g1, 2, 6, 21);
insert_edge(g1, 3, 4, 20);
insert_edge(g1, 3, 5, 8);
insert_edge(g1, 3, 6, 12);
insert_edge(g1, 3, 7, 12);
insert_edge(g1, 3, 8, 16);
insert_edge(g1, 4, 5, 19);
insert_edge(g1, 5, 7, 11);
insert_edge(g1, 6, 8, 11);
insert_edge(g1, 7, 8, 9);
kruskal_mst(g1, 9);
printf("----------------------------------------------------\n");
free(g1);
return 0;
}