[Data Structure] 이진 탐색 트리
2021. 12. 15. 18:23ㆍMajor`/자료구조
이진 탐색 트리

- root 기준으로 왼쪽 → root보다 작은 값
- root 기준으로 오른쪽 → root보다 큰 값
- 중위 순회 → 오름차순으로 정렬된 값 반환
1. 탐색 연산
- node == NULL || key == node->key → 해당 node 리턴
- key < node->key → node = node->llink를 통해서 왼쪽 서브트리 탐색
- key > node->key → node = node->rlink를 통해서 오른쪽 서브트리 탐색
- 순환 탐색 vs 반복 탐색 → 효율성 : 반복
treenode* search_recur(treenode* node, element data) {
// 순환 탐색 함수
if (node == NULL || node->data == data) return node;
else if (data < node->data) search_recur(node->left, data);
else search_recur(node->right, data);
}
treenode* search_iter(treenode* node, element data) {
// 반복 탐색 함수
while (node != NULL) {
if (data == node->data) return node;
else if (data < node->data) node = node->left;
else node = node->right;
}
return node;
}
2. 삽입 연산
- 탐색해가면서 각 root를 가리키는 cur / cur가 이전에 가리키고 있는 노드를 가리키는 pre
- Tree에 노드가 없을 경우 → new_node를 root로 설정
- insert하려는 key를 cur->data를 기준으로
- → 작으면 (key<cur->data) : 왼쪽 서브트리 탐색 (cur이 NULL이 될 때 까지)
- → 크면 (key>cur->data) : 오른쪽 서브트리 탐색 (cur이 NULL이 될 때 까지)
- 탐색 중, key == cur->data일 경우 → 이미 있는 key이기 때문에 insert 불가 → 함수 종료
- 탐색을 완료하고, key < pre->data일 경우 → pre->left에 new_node 삽입
- 탐색을 완료하고, key > pre->data일 경우 → pre->right에 new_node 삽입
void insert_node(treenode** root, element data) {
treenode* new_node = (treenode*)malloc(sizeof(treenode));
new_node->data = data; new_node->left = NULL; new_node->right = NULL;
treenode* cur = *root; // 현재 root, 진행해가면서 계속 바뀜
treenode* pre = NULL; // cur가 이전에 가리키고 있는 노드
if (cur == NULL) { // tree에 아무 노드도 없을 때
*root = new_node;
return;
}
else {
while (cur != NULL) {
pre = cur;
if (data == cur->data) {
printf("%d : 이미 존재하기 때문에 insert 실패\n\n", cur->data);
return; // data가 이미 존재하면 함수 종료
}
else if (data < cur->data)
cur = cur->left; // 왼쪽 서브트리로
else
cur = cur->right; // 오른쪽 서브트리로
}
if (data < pre->data)
pre->left = new_node; // pre의 left자식에 new_node 삽입
else
pre->right = new_node; // pre의 right자식에 new_node 삽입
}
}
※ Example
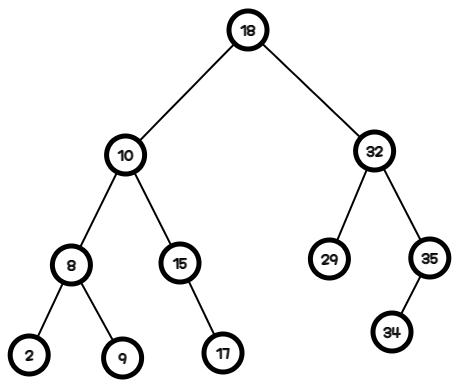
- (1) new_node->data (14)를 insert 할 때, cur, pre의 변화
| pre | NULL | node(18) | node(10) | node(15) |
| cur | node(18) | node(10) | node(15) | NULL (node(15)의 left) |
- data (14)는 현재 pre->data인 15보다 작기 때문에 pre->left에 new_node가 삽입된다
- (2) new_node->data (8)를 insert할 때, cur, pre의 변화
| pre | NULL | node(18) | node(10) |
| cur | node(18) | node(10) | node(8) - new_node->data와 cur->data가 같기 때문에 insert되지 못하고 그대로 함수 종료 |
3. 삭제 연산
- 탐색해가면서 각 root를 가리키는 cur
- cur가 이전에 가리키고 있는 노드를 가리키는 pre
- cur의 서브트리들을 가리키는 child
- 후계자를 가리키는 succ
- succ가 이전에 가리키고 있는 노드를 가리키는 succ_pre
while (cur != NULL && cur->data != key) {
// 트리가 비어있지 않고, cur->data가 key가 아닐동안 (삭제해야할 key 못찾을 동안)
pre = cur;
cur = (key < cur->data) ? cur->left : cur->right;
}- 삭제하려는 key를 가지고 있는 node 탐색
① 삭제하려는 노드가 단말노드일 경우

- 삭제하려는 node의 pre의 link를 끊으면 된다 (NULL로 설정)
if (cur->left == NULL && cur->right == NULL) {
// 삭제하려는 node가 단말노드일 경우
if (pre == NULL) { // Tree에 해당 node 하나만 존재할 경우
cur = NULL;
}
else {
// 17
// 11 32
// 11 or 32삭제 -> pre = node(17) 가리킴
if (pre->left == cur) { // cur = node(11) 가리킬 경우
pre->left = NULL;
}
else { // cur = node(32) 가리킬 경우
pre->right = NULL;
}
}
}
② 삭제하려는 노드가 1개의 서브트리를 가지고 있을 경우

- 삭제하려는 node의 pre의 link를 child를 가리키게 하면 된다
- child : 삭제하려는 node(cur)의 서브트리를 가리키는 포인터
else if (cur->left == NULL || cur->right == NULL) {
// 삭제 하려는 node가 서브트리 1개를 가지고 있을 경우
child = (cur->left != NULL) ? cur->left : cur->right;
// 삭제 하려는 node(cur)가 왼쪽 서브트리 갖고 있으면 child = cur->left
// 오른쪽 서브트리 갖고 있으면 child = cur->right
if (pre == NULL) {
// 35(cur)삭제 | 35(cur)삭제
// 20 | 50
cur = child;
}
else {
if (pre->right == cur)
// 35(pre) | 35(pre)
// 68(cur)삭제 | 68(cur)삭제
// 45 | 90
pre->right = child;
else
// 35(pre) | 35(pre)
// 20(cur)삭제 | 20(cur)삭제
// 15 | 26
pre->left = child;
}
}
③ 삭제하려는 노드가 2개의 서브트리를 가지고 있을 경우

- node 18을 삭제할 경우
- 후계자 대상 노드 = 왼쪽 서브트리에서 가장 큰 값 or 오른쪽 서브트리에서 가장 작은 값
- 삭제하려는 node를 후계자로 바꾸면 된다
else {
// 삭제하려는 node가 2개의 서브트리를 가질 경우
// 삭제 node의 후계자 -> 왼쪽 서브트리에서 가장 큰 값 or 오른쪽 서브트리에서 가장 작은 값
succ_pre = cur;
succ = cur->right;
while (succ->left != NULL) {
succ_pre = succ;
succ = succ->left;
}
if (succ_pre->left == succ) succ_pre->left = succ->right;
else succ_pre->right = succ->right;
cur->data = succ->data;
cur = succ;
}
※ Example
#include <stdio.h>
#include <stdlib.h>
// 이진 탐색 트리
#define max(a, b) ((a>b)?a:b)
typedef int element;
typedef struct treenode {
element data;
struct treenode* left;
struct treenode* right;
}treenode;
treenode n1 = { 2, NULL, NULL };
treenode n2 = { 9, NULL, NULL };
treenode n3 = { 17, NULL, NULL };
treenode n4 = { 34, NULL, NULL };
treenode n5 = { 8, &n1 , &n2 };
treenode n6 = { 15, NULL, &n3 };
treenode n7 = { 29, NULL, NULL };
treenode n8 = { 35, &n4, NULL };
treenode n9 = { 10, &n5, &n6 };
treenode n10 = { 32, &n7, &n8 };
treenode n11 = { 18, &n9, &n10 };
treenode* root = &n11;
void inorder(treenode* root) {
if (root != NULL) {
inorder(root->left);
printf("[%d] ", root->data);
inorder(root->right);
}
}
treenode* search_recur(treenode* node, element key) {
// 순환 탐색 함수
if (node == NULL || node->data == key) return node;
else if (key < node->data) search_recur(node->left, key);
else search_recur(node->right, key);
}
treenode* search_iter(treenode* node, element key) {
// 반복 탐색 함수
while (node != NULL) {
if (key == node->data) return node;
else if (key < node->data) node = node->left;
else node = node->right;
}
return node;
}
void insert_node(treenode** root, element key) {
treenode* new_node = (treenode*)malloc(sizeof(treenode));
new_node->data = key; new_node->left = NULL; new_node->right = NULL;
treenode* cur = *root; // 현재 root, 진행해가면서 계속 바뀜
treenode* pre = NULL; // cur가 이전에 가리키고 있는 노드
if (cur == NULL) { // tree에 아무 노드도 없을 때
*root = new_node;
return;
}
else {
while (cur != NULL) {
pre = cur;
if (key == cur->data) {
printf("%d : 이미 존재하기 때문에 insert 실패\n\n", cur->data);
return; // data가 이미 존재하면 함수 종료
}
else if (key < cur->data)
cur = cur->left; // 왼쪽 서브트리로
else
cur = cur->right; // 오른쪽 서브트리로
}
if (key < pre->data)
pre->left = new_node; // pre의 left자식에 new_node 삽입
else
pre->right = new_node; // pre의 right자식에 new_node 삽입
}
}
void delete_node(treenode** root, element key) {
treenode* cur, * pre, * child, * succ, * succ_pre;
cur = *root;
pre = NULL;
if (cur == NULL) {
// 트리가 비어있을 경우
printf("트리가 비어있기 때문에 delete 불가\n\n");
return;
}
else {
while (cur != NULL && cur->data != key) {
// 트리가 비어있지 않고, cur->data가 key가 아닐동안 (삭제해야할 key 못찾을 동안)
pre = cur;
cur = (key < cur->data) ? cur->left : cur->right;
}
if (cur == NULL) {
printf("%d : Tree에 존재 X\n\n", key);
return;
}
else {
if (cur->left == NULL && cur->right == NULL) {
// 삭제하려는 node가 단말노드일 경우
if (pre == NULL) { // Tree에 해당 node 하나만 존재할 경우
cur = NULL;
}
else {
// 17
// 11 32
// 11 or 32삭제 -> pre = node(17) 가리킴
if (pre->left == cur) { // cur = node(11) 가리킬 경우
pre->left = NULL;
}
else { // cur = node(32) 가리킬 경우
pre->right = NULL;
}
}
}
else if (cur->left == NULL || cur->right == NULL) {
// 삭제 하려는 node가 서브트리 1개를 가지고 있을 경우
child = (cur->left != NULL) ? cur->left : cur->right;
// 삭제 하려는 node(cur)가 왼쪽 서브트리 갖고 있으면 child = cur->left
// 오른쪽 서브트리 갖고 있으면 child = cur->right
if (pre == NULL) {
// 35(cur)삭제 | 35(cur)삭제
// 20 | 50
cur = child;
}
else {
if (pre->right == cur)
// 35(pre) | 35(pre)
// 68(cur)삭제 | 68(cur)삭제
// 45 | 90
pre->right = child;
else
// 35(pre) | 35(pre)
// 20(cur)삭제 | 20(cur)삭제
// 15 | 26
pre->left = child;
}
}
else {
// 삭제하려는 node가 2개의 서브트리를 가질 경우
// 삭제 node의 후계자 -> 왼쪽 서브트리에서 가장 큰 값 or 오른쪽 서브트리에서 가장 작은 값
succ_pre = cur;
succ = cur->right;
while (succ->left != NULL) {
succ_pre = succ;
succ = succ->left;
}
if (succ_pre->left == succ) succ_pre->left = succ->right;
else succ_pre->right = succ->right;
cur->data = succ->data;
cur = succ;
}
}
}
}
int get_tree_node(treenode* root) {
int count = 0;
if (root != NULL)
count = 1 + get_tree_node(root->left) + get_tree_node(root->right);
return count;
}
int get_terminal_node(treenode* root) {
int count = 0;
if (root != NULL){
if (root->left == NULL && root->right == NULL) return 1;
else
count = get_terminal_node(root->left) + get_terminal_node(root->right);
}
return count;
}
int get_height(treenode* root) {
int height = 0;
if (root != NULL)
height =1+ max(get_height(root->left), get_height(root->right));
return height;
}
int main(void) {
treenode* root2 = NULL;
printf("중위 순회 : ");
inorder(root);
printf("\n\n");
printf("노드 개수 : %d\n\n", get_tree_node(root));
printf("단말 노드 개수 : %d\n\n", get_terminal_node(root));
printf("트리 높이 : %d\n\n", get_height(root));
printf("----------------------------------------------\n\n");
printf(">> 탐색 연산\n\n");
printf("Tree 안에 10 존재 유무 : ");
if (search_recur(root, 10) == NULL)
printf("NO..\n\n");
else
printf("Yes!!\n\n");
printf("Tree 안에 50 존재 유무 : ");
if (search_recur(root, 50) == NULL)
printf("NO..\n\n");
else
printf("Yes!!\n\n");
printf("----------------------------------------------\n\n");
printf(">> 삽입 연산\n\n");
printf("## insert 15\n\n");
insert_node(&root, 15);
inorder(root);
printf("\n\n## insert 100\n\n");
insert_node(&root, 100);
inorder(root);
printf("\n\n");
printf("## insert 27\n\n");
insert_node(&root, 27);
inorder(root);
printf("\n\n");
printf("----------------------------------------------\n\n");
printf(">> 삭제 연산\n\n");
printf("## delete 200\n\n");
delete_node(&root, 200);
inorder(root);
printf("\n\n## delete 18\n\n");
delete_node(&root, 18);
inorder(root);
printf("\n\n");
printf("## delete 32\n\n");
delete_node(&root, 32);
inorder(root);
printf("\n\n");
printf("## delete 2\n\n");
delete_node(&root, 2);
inorder(root);
printf("\n\n");
printf("## delete 100\n\n");
delete_node(&root, 100);
inorder(root);
printf("\n\n");
return 0;
}
